dijkstra 两点的最短路径 单源 最短路径

思路以dist数组 来扩充  路径的访问，不断的刷新dist数组

设置一个顶点的集合s，并不断地扩充这个集合，一个顶点属于集合s当且仅当从源点到该点的路径已求出。开始时s中仅有源点，并且调整非s中点的最短路径长度，找当前最短路径点，将其加入到集合s，直到终点在s中。
基本步骤：
1、把所有结点分成两组：
      第一组：包括已经确定最短路径的结点；
      第二组：包括尚未确定最短路径的结点。
2、开始时，第一组只包含起点，第二组包含剩余的点；
3、用贪心的策略，按最短路径长度递增的顺序把第二组的结点加到第一组去，直到v0可达的所有结点都包含于第一组中。在这个过程中，不断更新最短路径，总保持从v0到第一组各结点的最短路径长度dist都不大于从v0到第二组任何结点的路径长度。
4、每个结点对应一个距离值，第一组结点对应的距离就是v0到此结点的最短路径长度，第二组结点对应的距离值就是v0由第一组结点到此结点的最短路径长度。
5、直到所有的顶点都扫描完毕（v0可达的所有结点都包含于第一组中），找到v0到其它各点的所有最短路径。

如图：求0点到其他点的最短路径。

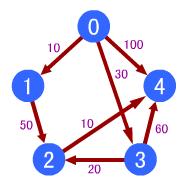
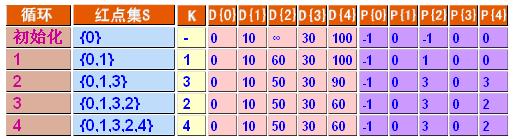
(1)开始时，s1={v0},s2={v1,v2,v3,v4}，v0到各点的最短路径是{0,10,&,30,100};
(2)在还未进入s1的顶点之中，最短路径为v1，因此s1={v0,v1},由于v1到v2有路径，因此v0到各点的最短路径更新为{0,10,60,30,100};
(3)在还未进入s1的顶点之中，最短路径为v3，因此s1={v0,v1,v3},由于v3到v2、v4有路径，因此v0到各点的最短路径更新为{0,10,50,30,90}；
(4)在还未进入s1的顶点之中，最短路径为v2，因此s1={v0,v1,v3,v2},由于v2到v4有路径，因此v0到各点的最短路径更新为{0,10,50,30,60};
数据结构：
(1)用一个二维数组a[i..j,i..j]来存储各点之间的距离，0x7fffffff表示无通路：

(2)用数组dist[i..j]表示最短路径；
(3)用集合s表示找到最短路径的结点。   

<转  http://www.cnblogs.com/Soul-ice-ACM/articles/2140221.html >

松弛原理

#include<cstdio>
#include<queue>
#include<vector>
#include<map>
#include<string>
#include<iostream>
#include<cmath>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
#define INF 0x7fffffff
#define LL __int64

const int maxn=;
int mpt[maxn][maxn];
int vis[maxn];
int m,n;
int dist[maxn];//从起点到其他点的最短距离

int dijkstra()
{
    int start,end;
    start=;end=n;
    for(int i=;i<=n;i++)
        dist[i]=mpt[start][i];
    vis[]=;
    while(true)
    {
        //第一步
        //找出与起点集合相连的最短边
        int minx=INF;
        int v;
        for(int i=;i<=n;i++)
        {
            if(dist[i]<minx&&vis[i]==)
            {
                minx=dist[i];
                v=i;
            }
        }
        if(minx>=INF)break;//如果所有点都在起点集合内
        vis[v]=;
        //松弛、更新DIST数组
        for(int i=;i<=n;i++)
        {
            if(vis[i]==&&dist[i]>dist[v]+mpt[v][i]&&dist[v]<INF&&mpt[v][i]<INF)
            {
                dist[i]=dist[v]+mpt[v][i];
            }
        }
    }
    return dist[end];
}

void init()
{
    memset(vis,,sizeof(vis));
    for(int i=;i<=n;i++)
    {
        for(int j=;j<=n;j++)
        {
            if(i==j)mpt[i][j]=;
            else
                mpt[i][j]=INF;
        }
    }
}

int main()
{

    while(scanf("%d%d",&n,&m)!=EOF)
    {
        if(n==&&m==)break;
        init();
        //建图
        for(int i=;i<=m;i++)
        {
            int a,b,c;
            scanf("%d%d%d",&a,&b,&c);
            if(c<mpt[a][b])
            {
                mpt[a][b]=c;
                mpt[b][a]=c;
            }
        }
        printf("%d\n",dijkstra());
    }

    return ;
}