【刷题】UOJ #171 【WC2016】挑战NPC

小 N 最近在研究 NP 完全问题，小 O 看小 N 研究得热火朝天，便给他出了一道这样的题目：

有 \(n\) 个球，用整数 \(1\) 到 \(n\) 编号。还有 \(m\) 个筐子，用整数 \(1\) 到 \(m\) 编号。

每个筐子最多能装 3 个球。

每个球只能放进特定的筐子中。具体有 \(e\) 个条件，第 \(i\) 个条件用两个整数 \(vi\) 和 \(ui\) 描述，表示编号为 \(vi\) 的球可以放进编号为 \(ui\) 的筐子中。

每个球都必须放进一个筐子中。如果一个筐子内有不超过 \(1\) 个球，那么我们称这样的筐子为半空的。

求半空的筐子最多有多少个，以及在最优方案中，每个球分别放在哪个筐子中。

小 N 看到题目后瞬间没了思路，站在旁边看热闹的小 I 嘿嘿一笑：“水题！”

然后三言两语道出了一个多项式算法。

小 N 瞬间就惊呆了，三秒钟后他回过神来一拍桌子：

“不对！这个问题显然是 NP 完全问题，你算法肯定有错！”

小 I 浅笑：“所以，等我领图灵奖吧!”

小 O 只会出题不会做题，所以找到了你——请你对这个问题进行探究，并写一个程序解决此题。

输入格式

第一行包含 \(1\) 个正整数 \(T\) ，表示有 \(T\) 组数据。

对于每组数据，第一行包含 \(3\) 个正整数 \(n,m,e\) ，表示球的个数，筐子的个数和条件的个数。

接下来 \(e\) 行，每行包含 \(2\) 个整数 \(vi,ui\) ，表示编号为 \(vi\) 的球可以放进编号为 \(ui\) 的筐子。

输出格式

对于每组数据，先输出一行，包含一个整数，表示半空的筐子最多有多少个。

然后再输出一行，包含 \(n\) 个整数 \(p1,p2,…,pn\) ，相邻整数之间用空格隔开，表示一种最优解。其中 \(pi\) 表示编号为 \(i\) 的球放进了编号为 \(pi\) 的筐子。如果有多种最优解,可以输出其中任何一种。

样例一

input

1

4 3 6

1 1

2 1

2 2

3 2

3 3

4 3

output

2

1 2 3 3

样例二

见样例数据下载。

限制与约定

对于所有数据，\(T≤5\) ，\(1≤n≤3m\) 。保证 \(1≤vi≤n,1≤ui≤m\) ，且不会出现重复的条件。

保证至少有一种合法方案,使得每个球都放进了筐子，且每个筐子内球的个数不超过 \(3\) 。

各测试点满足以下约定：

测试点编号	$m$	约定
$1$	$\leq 10$	$n \leq 20,e \leq 25$
$2$
$3$	$\leq 100$	$e=nm$
$4$		存在方案使得有 $m$ 个半空的筐子
$5$		不存在有半空的筐子的方案
$6$
$7$		无
$8$
$9$
$10$

时间限制： 1s

空间限制： 256MB

题解

思路极其巧妙

我们把一个框分成三个点，并且把其中两个点连上一条边

那么一个球与一个框相连就变成了这样：

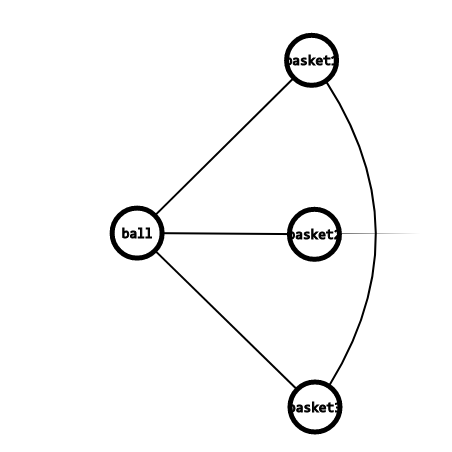
我们对这个图跑一遍带花树

那么如果只有一个球放进一个框中，这个框对应的三个点就只会有一个被匹配；而剩下的两个点因为有边相连，所以一定会相互匹配

也就是说，半空的框分出的三个点中一定在两个点相互匹配

因为题目保证球全部可以放进框中，所以匹配数一定大于等于 \(n\) ，而多出来的就是这些框分出的点自己的匹配

我们只要得出有多少自己的匹配，就知道有多少半空的框，用匹配的结果减去 \(n\) 就是答案了

要使答案最大，那么匹配的结果越大越好，所以就是跑带花树

#include<bits/stdc++.h>
#define ui unsigned int
#define ll long long
#define db double
#define ld long double
#define ull unsigned long long
#define ball(a,b) ((a-1)*3+b+n)
const int MAXN=300+10,MAXM=100+10,inf=0x3f3f3f3f;
int e,n,m,fa[MAXN<<1],beg[MAXN<<1],level[MAXN<<1],to[MAXN*MAXN*8],nex[MAXN*MAXN*8],link[MAXN<<1],pre[MAXN<<1],clk,vis[MAXN<<1];
std::queue<int> q;
template<typename T> inline void read(T &x)
{
	T data=0,w=1;
	char ch=0;
	while(ch!='-'&&(ch<'0'||ch>'9'))ch=getchar();
	if(ch=='-')w=-1,ch=getchar();
	while(ch>='0'&&ch<='9')data=((T)data<<3)+((T)data<<1)+(ch^'0'),ch=getchar();
	x=data*w;
}
template<typename T> inline void write(T x,char ch='\0')
{
	if(x<0)putchar('-'),x=-x;
	if(x>9)write(x/10);
	putchar(x%10+'0');
	if(ch!='\0')putchar(ch);
}
template<typename T> inline void chkmin(T &x,T y){x=(y<x?y:x);}
template<typename T> inline void chkmax(T &x,T y){x=(y>x?y:x);}
template<typename T> inline T min(T x,T y){return x<y?x:y;}
template<typename T> inline T max(T x,T y){return x>y?x:y;}
inline int found(int x)
{
	if(fa[x]!=x)fa[x]=found(fa[x]);
	return fa[x];
}
inline void insert(int x,int y)
{
	to[++e]=y;
	nex[e]=beg[x];
	beg[x]=e;
	to[++e]=x;
	nex[e]=beg[y];
	beg[y]=e;
}
inline int LCA(int u,int v)
{
	for(clk++;;std::swap(u,v))
		if(u)
		{
			u=found(u);
			if(level[u]==clk)return u;
			level[u]=clk;u=pre[link[u]];
		}
}
inline void blossom(int u,int v,int lca)
{
	while(found(u)!=lca)
	{
		pre[u]=v,v=link[u];
		if(vis[v]==2)vis[v]=1,q.push(v);
		if(found(u)==u)fa[u]=lca;
		if(found(v)==v)fa[v]=lca;
		u=pre[v];
	}
}
inline int bfs(int s)
{
	for(register int i=1;i<=n+3*m;++i)fa[i]=i;
	memset(pre,0,sizeof(pre));
	memset(vis,0,sizeof(vis));
	while(!q.empty())q.pop();
	vis[s]=1;
	q.push(s);
	while(!q.empty())
	{
		int x=q.front();
		q.pop();
		for(register int i=beg[x];i;i=nex[i])
		{
			if(found(x)==found(to[i])||vis[to[i]]==2)continue;
			if(!vis[to[i]])
			{
				vis[to[i]]=2;
				pre[to[i]]=x;
				if(!link[to[i]])
				{
					for(register int p=to[i],las;p;p=las)las=link[pre[p]],link[p]=pre[p],link[pre[p]]=p;
					return 1;
				}
				vis[link[to[i]]]=1;q.push(link[to[i]]);
			}
			else
			{
				int lca=LCA(x,to[i]);
				blossom(x,to[i],lca);blossom(to[i],x,lca);
			}
		}
	}
	return 0;
}
int main()
{
	static int T,l,ans;
	read(T);
	while(T--)
	{
		e=ans=0;
		memset(beg,0,sizeof(beg));
		memset(link,0,sizeof(link));
		read(n);read(m);read(l);
		for(register int i=1;i<=l;++i)
		{
			int u,v;read(u);read(v);
			for(register int k=1;k<=3;++k)insert(u,ball(v,k));
		}
		for(register int i=1;i<=m;++i)insert(ball(i,1),ball(i,3));
		for(register int i=1;i<=n+3*m;++i)
			if(!link[i])ans+=bfs(i);
		write(ans-n,'\n');
		for(register int i=1;i<=n;++i)write((link[i]-n+2)/3,' ');
		puts("");
	}
	return 0;
}