【bzoj4518】[Sdoi2016]征途 斜率优化dp

原文地址：http://www.cnblogs.com/GXZlegend/p/6812435.html

---

题目描述

Pine开始了从S地到T地的征途。

从S地到T地的路可以划分成n段，相邻两段路的分界点设有休息站。

Pine计划用m天到达T地。除第m天外，每一天晚上Pine都必须在休息站过夜。所以，一段路必须在同一天中走完。

Pine希望每一天走的路长度尽可能相近，所以他希望每一天走的路的长度的方差尽可能小。

帮助Pine求出最小方差是多少。

设方差是v，可以证明，v×m^2是一个整数。为了避免精度误差，输出结果时输出v×m^2。

输入

第一行两个数 n、m。

第二行 n 个数，表示 n 段路的长度

输出

一个数，最小方差乘以 m^2 后的值

样例输入

5 2
1 2 5 8 6

样例输出

36

---

题解

斜率优化（不需要二维）

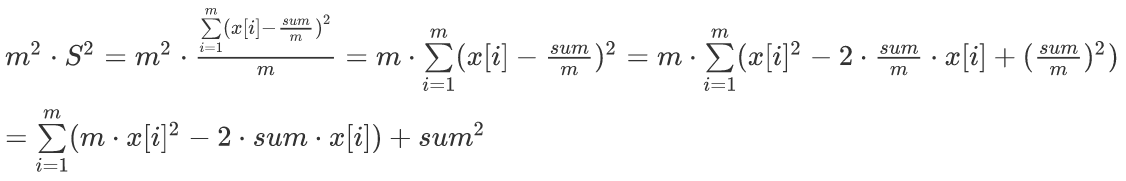
所以只要维护∑m*x[i^2-2*sum*x[i]的最小值即可。

设f[i][j]为前i条路分为j段的∑最小值，那么显然有f[i][j]=f[k][j-1]+m*(sum[i]-sum[k])*(sum[i]-sum[k])-2*sum[n]*(sum[i]-sum[k])。

这样dp时间复杂度为O(n^2*m)，会TLE，需要优化。

将上述dp方程平方展开并移项，得到f[k][j-1]+m*sum[j]^2+2*sum[n]*sum[j]=2*m*sum[i]*sum[j]+f[i][j]-m*sum[i]^2+2*sum[n]*sum[i]

这样可以用斜率优化来优化。

由于第二维j的存在，需要先循环第二维j，再循环第一维i，并将每次的f[i][j-1]与队列中元素比较并插入。

代码中可以看到我开了滚动数组，但好像没什么必要，直接开二维就行。

#include <cstdio>
#include <cstring>
#include <algorithm>
#define N 3010
#define y(i , p) (f[i][p] + m * sum[i] * sum[i] + 2 * sum[n] * sum[i])
using namespace std;
typedef long long ll;
int q[N];
ll a[N] , sum[N] , f[N][2];
int main()
{
    int n , m , i , j , l , r , d;
    scanf("%d%d" , &n , &m);
    for(i = 1 ; i <= n ; i ++ ) scanf("%lld" , &a[i]) , sum[i] = sum[i - 1] + a[i];
    for(i = 1 ; i <= n ; i ++ ) f[i][1] = m * sum[i] * sum[i] - 2 * sum[n] * sum[i];
    for(i = 2 ; i <= m ; i ++ )
    {
        l = r = 0 , d = i & 1;
        for(j = 1 ; j <= n ; j ++ )
        {
            while(l < r && y(q[l + 1] , d ^ 1) - y(q[l] , d ^ 1) < 2 * m * sum[j] * (sum[q[l + 1]] - sum[q[l]])) l ++ ;
            f[j][d] = y(q[l] , d ^ 1) - 2 * m * sum[j] * sum[q[l]] + m * sum[j] * sum[j] - 2 * sum[n] * sum[j];
            while(l < r && (y(j , d ^ 1) - y(q[r] , d ^ 1)) * (sum[q[r]] - sum[q[r - 1]]) < (sum[j] - sum[q[r]]) * (y(q[r] , d ^ 1) - y(q[r - 1] , d ^ 1))) r -- ;
            q[++r] = j;
        }
    }
    printf("%lld\n" , f[n][m & 1] + sum[n] * sum[n]);
    return 0;
}