UVa 221 Urban Elevations 城市正视图 离散化初步 无限化有限

转载请注明：

仰望高端玩家的小清新 http://www.cnblogs.com/luruiyuan/

题目大意：

题目传送门：UVa 221 Urban Elevations

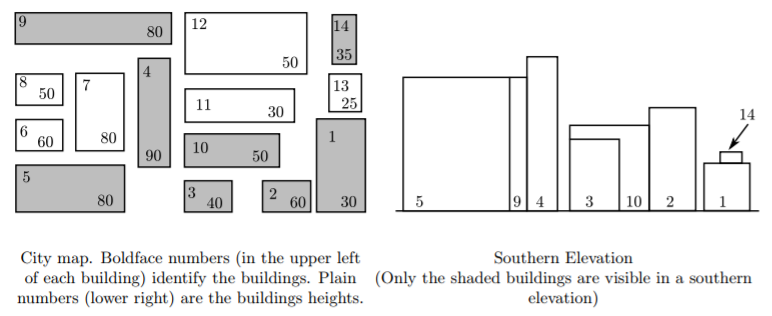
给出城市中建筑物的x, y 坐标的最小值：x,y ， 再给出其以左下角为坐标原点的关于x轴、y轴上的长度 w, 和 d，最后给出建筑物的高度 h，将建筑物的正视图中，能够看到的建筑物的id打印出来：要求先打印x小的，当x相同时，打印y小的。为了简化，假定建筑物都是长方体。同时，每个输出之间要用一个空行隔开 One blank line must separate output from consecutive input records.(一开始没注意审题，wa在这了┭┮﹏┭┮)

思路：

首先，这个题我本来没什么思路，还是不得不参考一波刘汝佳老师的思路

本题最大的收获是初步认识了 “离散化” ：将无限转化为有限的方法。

1. 首先，我们注意到，每个建筑物的深度在这里没有影响，因此深度是个干扰项
2. 一个关键点是，题目给定的数据是实数，即浮点数，因此我们不能穷举所有的x坐标来遍历，对于无穷问题，我们需要考虑离散化，化无穷为有限
3. 对于本题，离散化的关键在于，如何表示建筑物之间的互相重叠的关系
4. 必须注意到，每个建筑物有2个x坐标，一个是input中直接给出的x，而另一个是我们可以通过w+x得到的“右边的x坐标”
5. 通过2个坐标，我们可以首先对x去重，然后构建出相应的x轴的多个区间，这样，每一组重叠关系必然会落在我们的x区间之中。这也正是代码中x数组开2倍空间的原因，以及用途。
6. 我们只需在区间内任选一点，即可作为区间的整体代表元素，来判断某个建筑是否经过了此区间，因此，可以选择比较方便的区间中点。没有经过区间代表元素的，显然不会经过该区间。经过了第5步和这一步，我们就将一个无限问题，转化为有限问题了。
7. 对于每个建筑，我们考虑2点：是否经过了区间中点；是否存在y坐标小于它，且高度大于等于它的建筑。上述两点满足任何一点，则该建筑都不可见
8. 其他小细节：代码 53 行的  b[j].y < b[i].y  能够保证 i != j； 53行的判定语句的顺序也可以些微提高代码效率，比如将函数调用延迟到最后一个，以降低调用概率，降低平均运行时间；unique() 函数调用前必须首先排序，因为unique函数只能对相邻元素去重，这和unique的原理有关，话说，这里的unique函数真的没有python 里的 set() 好用啊。。。

代码如下：

 // UVa 221 Urban Elevations
 // Ruiyuan Lu
 #include<cstdio>
 #include<algorithm>
 using namespace std;

 const int maxn =  + ;
 double x[maxn*];    // each building has 2 coordinates of x axis
 int n;                // number of the buildings

 struct Building{
     int id;
     double x, y, w, d, h;                             // w: means x_len, d:depth means y_len, h:height
     bool operator < (const Building& b) const {        // sort for output
         return x < b.x || (x == b.x && y < b.y);
     }
 }b[maxn];

 bool cover(int i, double mx);        // determine if the mx is in the range of building's x coordinate
 bool visible(int i, double mx);        // i: the index of buildings; mx: middle x coordinate of an interval

 int main(){
     int cnt = ;
     while(scanf("%d", &n) ==  && n > ){
         for(int i=; i<n;i++){
             scanf("%lf%lf%lf%lf%lf", &b[i].x, &b[i].y, &b[i].w, &b[i].d, &b[i].h);
             b[i].id = i + ;
             x[i*] = b[i].x; x[i*+] = b[i].x + b[i].w;    // init x for discretization
         }
         sort(x, x+n*);                        // sort before unique() is invoked
         sort(b, b+n);                        // sort for output
         int m = unique(x, x+maxn*) - x;    // get the number of unique x in the array
         // print result
         if(cnt++)printf("\n");                // print the '\n' for last output
         printf("For map #%d, the visible buildings are numbered as follows:\n%d", cnt, b[].id);
         for(int i=;i<n;i++)
             for(int j=;j<m;j++)            // check each building if it is visible in any interval of m intervals
                 if(visible(i, (x[j-] + x[j]) / )){
                     printf(" %d", b[i].id);
                     break;
                 }
         printf("\n");                    // as they required: One blank line must separate output from consecutive input records.
     }
 }

 bool cover(int i, double mx){
     return b[i].x <= mx && b[i].x + b[i].w >= mx;
 }

 bool visible(int i, double mx){
     if(!cover(i, mx)) return false;
     for(int j=;j<n;j++)
         if(b[j].y < b[i].y && b[j].h >= b[i].h && cover(j, mx)) return false;
     return true;
 }

啦啦啦，今天就到这里啦~改天见*★,°*:.☆(￣▽￣)/$:*.°★* 。