Codeforces 550 D. Regular Bridge

\(>Codeforces \space 550 D. Regular Bridge<\)

题目大意 :给出 \(k\) ，让你构造出一张点和边都不超过 \(10^6\) 的无向图，使得每个点的度数都为 \(k\) 且至少有一条桥边。

\(1≤ k ≤ 100\)

解题思路 :

通过观察可以发现当 \(k\) 为偶数的时候必然无解

证明：先假设当 \(k\) 是偶数的时候可以构造出来。 那么对于这张图的每一条桥边，必然连接这两个联通块，那么单独考虑这两个联通块，有且仅有一个端点的度数是 \(k - 1\) ，其他点的度数都是 \(k\) 所以这个联通块的总度数为 \(kx - 1 (x > 0 )\) 因为k是偶数，所以总度数为奇数。但是对于任意一个无向图，它的度数之和都是偶数，所以产生矛盾，当 \(k\) 为偶数的情况下不存在解

考虑当 \(k\) 是奇数的时候如何构造这张图。

观察发现桥边的条数并不影响构造，所以可以只构造一条桥边的情况

问题就转化为构造两个子图，有一个点的度数为 \(k - 1\) 其余点的度数都为 \(k\)

按照这个方式画出 \(k = 3\) 的情况如下

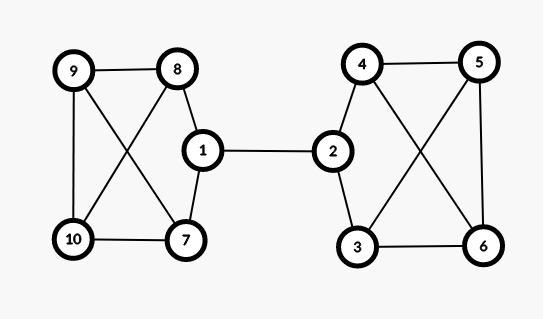
观察发现，对于每一个联通块，有 \(k-1\) 个点连向桥边端点，对于这 \(k-1\) 个点，每个点都连向另外 \(k-1\) 个点

由于 \(k\) 是奇数，\(k - 1\) 是偶数，所以另外 \(k - 1\) 个点可以相邻两两连边产生额外 \(1\) 的度数

加上连向桥边的 \(k - 1\) 个点提供的度数刚好是 \(k\) 所以按照 \(k = 3\) 的情况画可以推广到所有 \(k\) 是奇数的情况

由此可以得出构建方法 :

先构建一条桥边，对于两个端点分别做同样操作：

新建 \(k-1\) 个点，每个点向端点连边

再新建 \(k - 1\) 个点，每个点向相邻的点连边

对于两层点形成的二分图，两两之间连边

/*program by mangoyang*/
#include<bits/stdc++.h>
#define inf (0x7f7f7f7f)
#define Max(a, b) ((a) > (b) ? (a) : (b))
#define Min(a, b) ((a) < (b) ? (a) : (b))
typedef long long ll;
using namespace std;
template <class T>
inline void read(T &x){
    int f = 0, ch = 0; x = 0;
    for(; !isdigit(ch); ch = getchar()) if(ch == '-') f = 1;
    for(; isdigit(ch); ch = getchar()) x = x * 10 + ch - 48;
    if(f) x = -x;
}
vector<int> g[100005]; int m, k;
inline void makemid(int type){
	int rt = 1 + type;
	for(int i = 1; i < k; i++) g[rt].push_back(rt + i), m++;
	for(int i = rt + 1; i < rt + k; i++)
		for(int j = rt + k; j < rt + 2 * k - 1; j++) g[i].push_back(j), m++;
	for(int j = rt + k; j < rt + 2 * k - 1; j += 2) g[j].push_back(j + 1), m++;
}
int main(){
	read(k);
	if(k % 2 == 0) return puts("NO"), 0;
	makemid(0), makemid(2 * k - 1); g[1].push_back(2 * k), m++;
	puts("YES");
	cout << 4 * k - 2 << " " << m << endl;
	for(int i = 1; i <= 4 * k - 2; i++)
		for(int j = 0; j < g[i].size(); j++) cout << i << " " << g[i][j] << endl;
	return 0;
}