PTA L3-023 计算图 (dfs+数学推导)

“计算图”（computational graph）是现代深度学习系统的基础执行引擎，提供了一种表示任意数学表达式的方法，例如用有向无环图表示的神经网络。图中的节点表示基本操作或输入变量，边表示节点之间的中间值的依赖性。例如，下图就是一个函数 ( 的计算图。

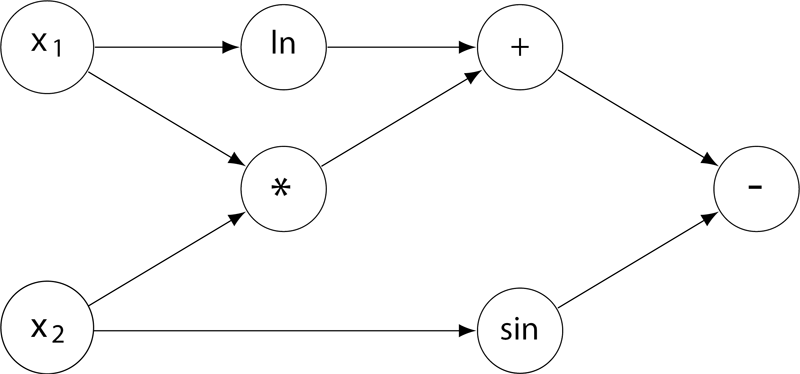
现在给定一个计算图，请你根据所有输入变量计算函数值及其偏导数（即梯度）。例如，给定输入,，上述计算图获得函数值 (；并且根据微分链式法则，上图得到的梯度 ∇。

知道你已经把微积分忘了，所以这里只要求你处理几个简单的算子：加法、减法、乘法、指数（ex，即编程语言中的 exp(x) 函数）、对数（ln，即编程语言中的 log(x) 函数）和正弦函数（sin，即编程语言中的 sin(x) 函数）。

友情提醒：

常数的导数是 0；x 的导数是 1；ex 的导数还是 ex；ln 的导数是 1；sin 的导数是 cos。
回顾一下什么是偏导数：在数学中，一个多变量的函数的偏导数，就是它关于其中一个变量的导数而保持其他变量恒定。在上面的例子中，当我们对 x1 求偏导数 / 时，就将 x2 当成常数，所以得到 ln 的导数是 1，x1x2 的导数是 x2，sin 的导数是 0。
回顾一下链式法则：复合函数的导数是构成复合这有限个函数在相应点的导数的乘积，即若有 (，(，则 /。例如对 sin 求导，就得到 cos。

如果你注意观察，可以发现在计算图中，计算函数值是一个从左向右进行的计算，而计算偏导数则正好相反。

输入格式：

输入在第一行给出正整数 N（≤），为计算图中的顶点数。

以下 N 行，第 i 行给出第 i 个顶点的信息，其中 ,。第一个值是顶点的类型编号，分别为：

0 代表输入变量
1 代表加法，对应 x1+x2
2 代表减法，对应 x1−x2
3 代表乘法，对应 x1×x2
4 代表指数，对应 ex
5 代表对数，对应 ln
6 代表正弦函数，对应 sin

对于输入变量，后面会跟它的双精度浮点数值；对于单目算子，后面会跟它对应的单个变量的顶点编号（编号从 0 开始）；对于双目算子，后面会跟它对应两个变量的顶点编号。

题目保证只有一个输出顶点（即没有出边的顶点，例如上图最右边的 -），且计算过程不会超过双精度浮点数的计算精度范围。

输出格式：

首先在第一行输出给定计算图的函数值。在第二行顺序输出函数对于每个变量的偏导数的值，其间以一个空格分隔，行首尾不得有多余空格。偏导数的输出顺序与输入变量的出现顺序相同。输出小数点后 3 位。

输入样例：

输出样例：

11.652

5.500 1.716

天梯赛L3的第二题，反向建图之后利用各种求导公式对每个变量分别跑一遍dfs求偏导就行了。场下30分钟过掉，场上的我真是宛如一个智障，~QAQ~

 #include<bits/stdc++.h>

 using namespace std;

 typedef long long ll;

 typedef double db;

 const int N=5e4+;

 int n,f[N],dg[N],s,nxt[N][],vis[N],x;

 db a[N],f1[N],f2[N];

 vector<int> vec;

 vector<db> ans;

 void dfs(int u) {

     if(vis[u])return;

     vis[u]=;

     if(f[u]==)f1[u]=a[u],f2[u]=u==x?:;

     else if(f[u]==) {

         int v1=nxt[u][],v2=nxt[u][];

         dfs(v1),dfs(v2);

         f1[u]=f1[v1]+f1[v2],f2[u]=f2[v1]+f2[v2];

     } else if(f[u]==) {

         int v1=nxt[u][],v2=nxt[u][];

         dfs(v1),dfs(v2);

         f1[u]=f1[v1]-f1[v2],f2[u]=f2[v1]-f2[v2];

     } else if(f[u]==) {

         int v1=nxt[u][],v2=nxt[u][];

         dfs(v1),dfs(v2);

         f1[u]=f1[v1]*f1[v2],f2[u]=f2[v1]*f1[v2]+f1[v1]*f2[v2];

     } else if(f[u]==) {

         int v=nxt[u][];

         dfs(v),f1[u]=exp(f1[v]),f2[u]=exp(f1[v])*f2[v];

     } else if(f[u]==) {

         int v=nxt[u][];

         dfs(v),f1[u]=log(f1[v]),f2[u]=f2[v]/f1[v];

     } else if(f[u]==) {

         int v=nxt[u][];

         dfs(v),f1[u]=sin(f1[v]),f2[u]=cos(f1[v])*f2[v];

     }

 }

 int main() {

     scanf("%d",&n);

     for(int i=; i<n; ++i) {

         scanf("%d",&f[i]);

         if(f[i]==) {

             scanf("%lf",&a[i]);

             vec.push_back(i);

         } else if(f[i]>=&&f[i]<=) {

             int u,v;

             scanf("%d%d",&u,&v);

             nxt[i][]=u,nxt[i][]=v,dg[u]++,dg[v]++;

         } else if(f[i]>=&&f[i]<=) {

             int u;

             scanf("%d",&u);

             nxt[i][]=u,dg[u]++;

         }

     }

     for(int i=; i<n; ++i)if(!dg[i])s=i;

     for(int i:vec)x=i,memset(vis,,sizeof vis),dfs(s),ans.push_back(f2[s]);

     printf("%.3f\n",f1[s]);

     for(int i=; i<ans.size(); ++i)printf("%.3f%c",ans[i]," \n"[i==ans.size()-]);

     return ;

 }