Fel表达式使用过程中需要注意的问题

精度问题：

我们知道java中直接使用float和double参与的计算都可能会产生精度问题，比如0.1+0.3、1.0-0.9 等。所以一般财务系统，都会使用BigDecimal进行加减乘除。 在调研Fel过程中，发现Fel里进行计算都是使用浮点数加减乘除的，所以不可避免的会产生精度问题。

Case+源码分析：

加法 Case：

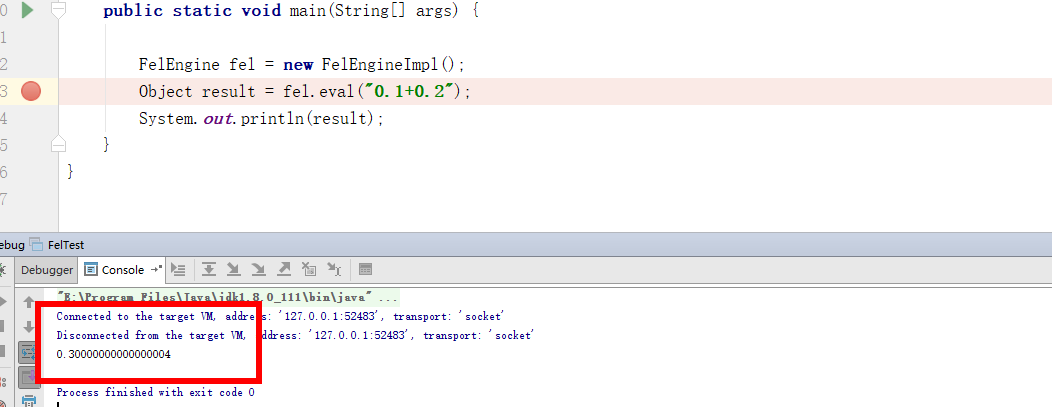
FelEngine fel = new FelEngineImpl();
Object result = fel.eval("0.1+0.2");
System.out.println(result);

源码分析：

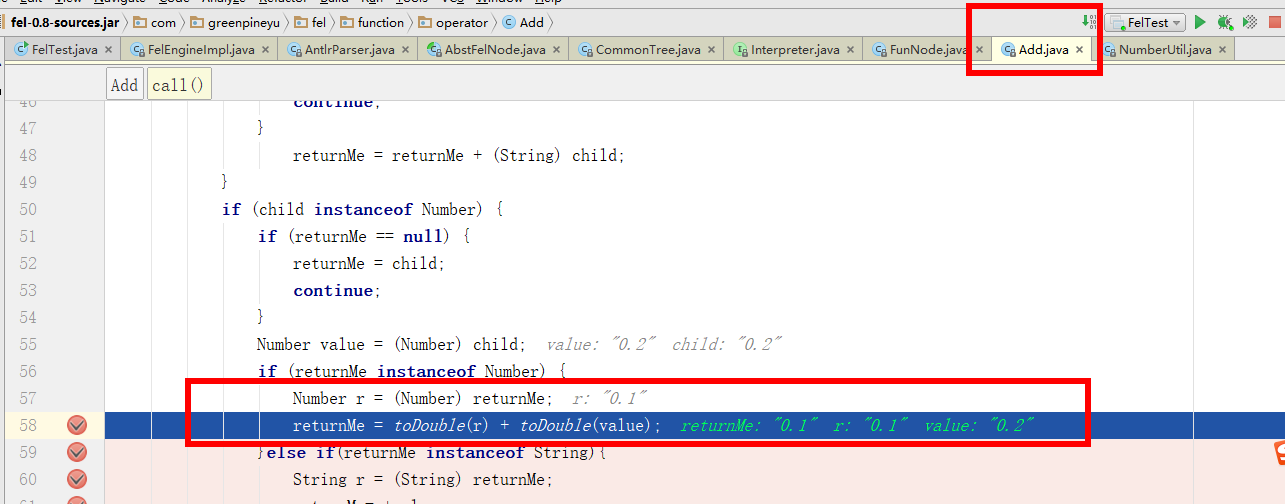
简单的来说，Fel首先经过词法解析器将表达式解析成FelNode实例，FelNode包含表达式子节点（比如+号、0.1等）和表达式解析器，解析器对应的有com.greenpineyu.fel.function.operator.Add、ccom.greenpineyu.fel.function.operator.Sub、com.greenpineyu.fel.function.operator.Mul、com.greenpineyu.fel.function.operator.Div等各种解析器（详见com.greenpineyu.fel.function.operator下的类），具体的表达式运算结果是由这些解析器计算的。具体到方法又是由com.greenpineyu.fel.function.operator.Add#call计算的。

public Object call(FelNode node, FelContext context) {
	Object returnMe = null;
	for (Iterator<FelNode> iterator = node.getChildren().iterator(); iterator.hasNext();) {
		Object child = iterator.next();
		if (child instanceof FelNode) {
			FelNode childNode = (FelNode) child;
			child = childNode.eval(context);
		}
		if (child instanceof String) {
			if (returnMe == null) {
				returnMe = child;
				continue;
			}
				returnMe = returnMe + (String) child;
		}
		if (child instanceof Number) {
			if (returnMe == null) {
				returnMe = child;
				continue;
			}
			Number value = (Number) child;
			if (returnMe instanceof Number) {
				Number r = (Number) returnMe;
				// 注意这里：是直接使用转成double进行加减的。
				returnMe = toDouble(r) + toDouble(value);
			}else if(returnMe instanceof String){
				String r = (String) returnMe;
				returnMe=r+value;
			}
		}
	}
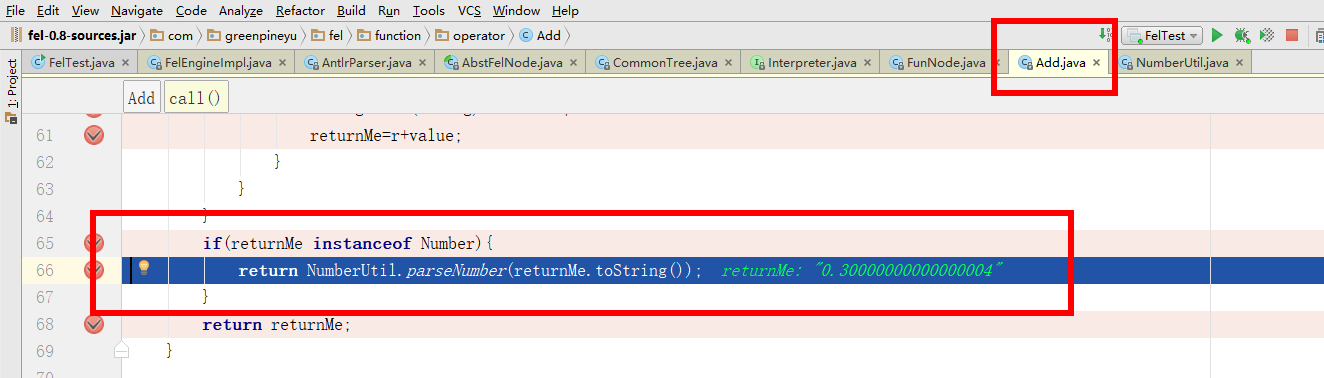
	if(returnMe instanceof Number){
		return NumberUtil.parseNumber(returnMe.toString());
	}
	return returnMe;
}

/**
 * 将Number转换成double
 * @param number
 * @return
 */
public static double toDouble(Number number){
	if(number instanceof Float){
		//float转double时，会出现精度问题。"(double)1.1f"的值类似于1.1000000476837158),
		//使用 Double.parseDouble(number.toString());则不会出现问题。
		return Double.parseDouble(number.toString());
	}
	return number.doubleValue();
}

通过上面的returnMe = toDouble(r) + toDouble(value); 代码片段，我们就知道Fel是拿double进行加法操作的，这样某些情况下就会产生精度问题。

其他运算操作同之。

解决办法：

避免使用浮点数进行数值计算，可以将操作数乘以10的某个倍数，将浮点数转成整数。至于从整数再转成浮点数就可以使用BigDecimal了。其实，一个好的财务系统都是不会存储和使用浮点数的，都是转成整数，只有在进行页面显示的时候才处理回浮点数。