Gym 100796B Wet Boxes（思维）题解

题意：给一个如图坐标系，每个方形都放在下面两个中间，已知一个木块湿了那么他下面所有的都会湿，显然，不能湿两次。问，每次给出一个坐标，把他弄湿，有几个木块从干变成湿了。

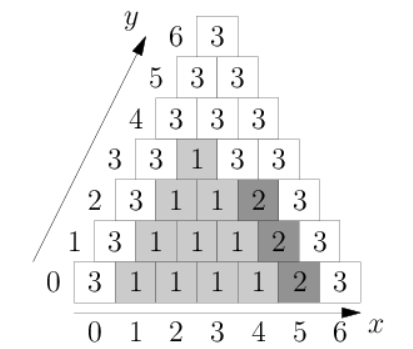
思路：我们把坐标系拉直，就变成了如图，显然我们弄湿 a（0,5），那么红色部分变湿，看一眼应该已经找到计算面积的方法了。所以我们每次得到一个坐标，我们就能直接算出面积。然后我们判断，是否已经有顶点所产生的面积包含了我的顶点，是的话我湿的面积为0。没有的话我就遍历一遍所有顶点，删掉所有的已经湿了的面积，剩下的就是新湿的面积了。

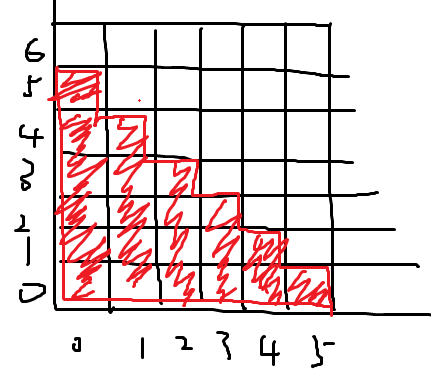
然后我们看一下，如果两个面积不相交，那么必有下图这样，我们可以简单的算出，红色最右边的x应该为a.x + a.y，那么不相交的条件为a.x + a.y < b.x。

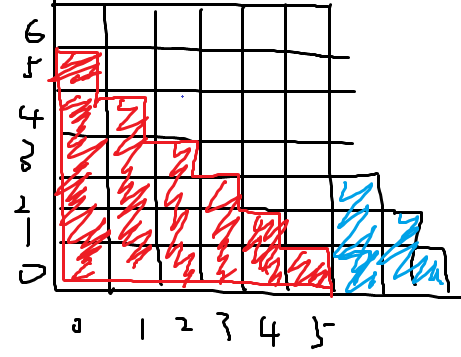
相含的时候，被包含的那个面积必然是从包含的面积内部一点为顶点，而红色内部所有的点都有一个性质x + y <= a.x + a.y && x >= a.x，所以以此判断包含关系。

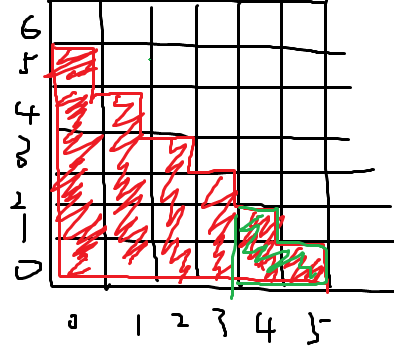
然后计算交集：显然交集为蓝色减去它内部小红色的面积。那么我们先判断是否有内含，有的话就是被含的面积；否则我们找出红色小面积的顶点，因为我们知道y的长度就可以算出面积，那么Y = a.x + a.y - b.x。

但是我们直接减去相交面积显然不行，因为可能有很多重复的面积被我减掉了。那怎么办？直接计算每次多减的加回去，多算的面积是两两之间的交集，一直加到最后一块和我相交的（也就是x >= a.x且不内含的第一块）。

代码：

#include<cmath>
#include<set>
#include<map>
#include<queue>
#include<cstdio>
#include<vector>
#include<cstring>
#include <iostream>
#include<algorithm>
#include<unordered_map>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int maxn = 1e5 + 10;
const int M = maxn * 30;
const ull seed = 131;
const int INF = 0x3f3f3f3f;
const int MOD = 1e4 + 7;
struct Tri{
    ll x, y;
    bool operator < (const Tri a) const{
        return x < a.x;
    }
};
set<Tri> s;
ll getAera(Tri a){
    return (1LL + a.y) * (a.y + 2LL) / 2LL;
}
bool contain(Tri a, Tri b){ //a包含b
    return a.x + a.y >= b.x + b.y && a.x <= b.x;
}
ll intersect(Tri a, Tri b){ //a b交集
    if(contain(a, b)) return getAera(b);
    else if(contain(b, a)) return getAera(a);
    else{
        ll y = -1;
        if(a.x <= b.x) y = max(y, a.x + a.y - b.x);
        else y = max(y, b.x + b.y - a.x);
        return getAera(Tri{1, y});
    }
}
int main(){
    int n;
    scanf("%d", &n);
    s.clear();
    while(n--){
        Tri a;
        scanf("%lld%lld", &a.x, &a.y);
        auto it = s.upper_bound(a);
        if(it != s.begin()) it--; //第一个x小于等于a.x的位置
        if(s.begin() != s.end() && contain(*it, a)){ //a被包含
            printf("0\n");
            continue;
        }
        ll ret = getAera(a);
        for(auto i = it; i != s.end();){
            ret -= intersect(a, *i);
            if(!contain(a, *i) && (*i).x >= a.x) break;
            auto pre = i++;
            if(i == s.end()) break;
            ret += intersect(*i, *pre);
        }
        for(auto i = it; i != s.end();){
            if(contain(a, *i)) s.erase(i++);
            else i++;
        }
        s.insert(a);
        printf("%lld\n", ret);
    }
    return 0;
}