JavaScript图形实例：Hilbert曲线
德国数学家David Hilbert在1891年构造了一种曲线，首先把一个正方形等分成四个小正方形，依次从西北角的正方形中心出发往南到西南正方形中心，再往东到东南角的正方形中心，再往北到东北角正方形中心，这是一次迭代；如果对四个小正方形继续上述过程，往下划分，反复进行，最终就得到一条可以填满整个正方形的曲线，这就是Hibert曲线。其生成过程如图1所示。
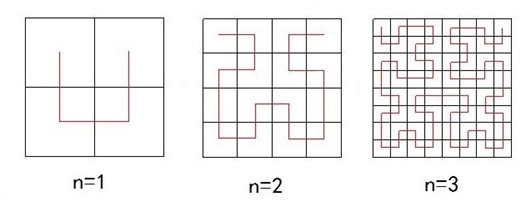
图1 Hilbert曲线的生成
Hilbert曲线可以采用递归过程实现，在递归处理时，连接中点的方式有4种，如图2所示。
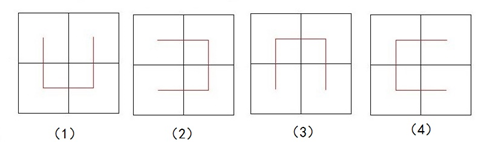
图2 连接中心点的4种方式
设正方形左上角的顶点坐标为（x1,y1），右下角顶点坐标为（x2,y2）。若将方式（3）的正方形左上角坐标置为（x2,y2），右下角坐标置为（x1,y1），则方式（3）等同于方式（1），相当于旋转180°；同理，方式（4）等同于方式（2）。因此，4种连接中心点的方式可以看成（1）和（2）两种。
两种连线方式的连线走向及下一次扩展的方式如图3所示。
图3 两种连线方式走向及扩展
其中，方式（1）的四个中心点坐标分别为：
①（x1+dx/4,y1+dy/4） ②（x1+dx/4, y1+3*dy/4）
③ （x1+3*dx/4, y1+3*dy/4） ④（x1+3*dx/4,y1+dy/4） （dx=x2-1,dy=y2-y1）
方式（2）的四个中心点坐标分别为：
①（x1+dx/4,y1+dy/4） ②（x1+3*dx/4,y1+dy/4）
③ （x1+3*dx/4, y1+3*dy/4） ④（x1+dx/4, y1+3*dy/4）
为此，引入一个标识变量s，s=1表示方式（1），s=-1表示方式（2），这样两种方式的中心点坐标可以统一表示为：
①（x1+dx/4,y1+dy/4） ②（x1+(2-s)*dx/4, y1+(2+s)*dy/4）
③（x1+3*dx/4, y1+3*dy/4） ④（x1+(2+s)*dx/4,y1+(2-s)*dy/4）
递归扩展时，方式（1）中4个小正方形的扩展方式分别是：方式（2）、方式（1）、方式（1）和方式（4）（注意：给定两个顶点坐标顺序调整后等同于方式（2））；方式（2）中4个小正方形的扩展方式分别是：方式（1）、方式（2）、方式（2）和方式（3）。
编写如下的HTML代码。
<!DOCTYPE html>
<head>
<title>Hilbert曲线</title>
</head>
<body>
<canvas id="myCanvas" width="500" height="500" style="border:3px double #996633;">
</canvas>
<script type="text/javascript">
var canvas = document.getElementById('myCanvas');
var ctx = canvas.getContext('2d');
var depth=5;
ctx.lineWidth = 2;
ctx.strokeStyle = "red";
ctx.beginPath();
ctx.moveTo(50+400/Math.pow(2,depth+1),50+400/Math.pow(2,depth+1));
drawShapes(depth,1,50,50,450,450);
ctx.stroke();
function drawShapes(n,s,x1,y1,x2,y2)
{
dx = x2 - x1,
dy = y2 - y1;
if (n>1)
{
if(s>0)
{
drawShapes(n-1,-1,x1,y1,(x1+x2)/2,(y1+y2)/2);
drawShapes(n-1,1,x1,(y1+y2)/2,(x1+x2)/2,y2);
drawShapes(n-1,1,(x1+x2)/2,(y1+y2)/2,x2,y2);
drawShapes(n-1,-1,x2,(y1+y2)/2,(x1+x2)/2,y1);
}
else
{
drawShapes(n-1,1,x1,y1,(x1+x2)/2,(y1+y2)/2);
drawShapes(n-1,-1,(x1+x2)/2,y1,x2,(y1+y2)/2);
drawShapes(n-1,-1,(x1+x2)/2,(y1+y2)/2,x2,y2);
drawShapes(n-1,1,(x1+x2)/2,y2,x1,(y1+y2)/2);
}
}
if (n==1)
{
ctx.lineTo(x1+dx/4,y1+dy/4);
ctx.lineTo(x1+(2-s)*dx/4, y1+(2+s)*dy/4);
ctx.lineTo(x1+3*dx/4, y1+3*dy/4);
ctx.lineTo(x1+(2+s)*dx/4,y1+(2-s)*dy/4);
}
}
</script>
</body>
</html>
在浏览器中打开包含这段HTML代码的html文件，可以看到在浏览器窗口中绘制出如图4所示的Hilbert曲线。
图4 递归深度maxdepth =5的Hilbert曲线
上面的程序需要推出方式（一）和方式（二）的坐标统一形式，还需注意方式（3）和方式（4）与方式（一）和方式（二）的同一性。
由于Hilbert曲线可以看成是4种方式进行组合，因此可以直接对4种方式编写递归过程。编写如下的HTML文件。
<!DOCTYPE html>
<head>
<title>Hilbert曲线</title>
</head>
<body>
<canvas id="myCanvas" width="500" height="500" style="border:3px double #996633;">
</canvas>
<script type="text/javascript">
var canvas = document.getElementById('myCanvas');
var ctx = canvas.getContext('2d');
ctx.lineWidth = 2;
ctx.strokeStyle = "red";
ctx.beginPath();
var depth=5; // 递归深度
var h=400/Math.pow(2,depth);
var x = 50+h;
var y = 50+h;
ctx.moveTo(x,y);
One(depth);
ctx.stroke();
function One(n) // 方式（1）的递归调用
{
if(n > 0)
{
Two(n-1);
ctx.lineTo(x, y+h); y+=h;
One(n-1);
ctx.lineTo(x+h, y); x+=h;
One(n-1);
ctx.lineTo(x, y-h); y-=h;
Four(n-1);
}
}
function Two(n) // 方式（2）的递归调用
{
if(n > 0)
{
One(n-1);
ctx.lineTo(x+h, y); x+=h;
Two(n-1);
ctx.lineTo(x, y+h); y+=h;
Two(n-1);
ctx.lineTo(x-h, y); x-=h;
Three(n-1);
}
}
function Three(n) // 方式（3）的递归调用
{
if(n > 0)
{
Four(n-1);
ctx.lineTo(x, y-h); y-=h;
Three(n-1);
ctx.lineTo(x-h, y); x-=h;
Three(n-1);
ctx.lineTo(x, y+h); y+=h;
Two(n-1);
}
}
function Four(n) // 方式（4）的递归调用
{
if(n > 0)
{
Three(n-1);
ctx.lineTo(x-h,y); x-=h;
Four(n-1);
ctx.lineTo(x, y-h); y-=h;
Four(n-1);
ctx.lineTo(x+h, y); x+=h;
One(n-1);
}
}
</script>
</body>
</html>
在浏览器中打开包含这段HTML代码的html文件，可以看到在浏览器窗口中绘制出如图5所示的Hilbert曲线。
图5 调用One(depth)时绘制的图形
将程序中的调用语句“One(depth)”改写成“Two(depth)”，则在浏览器窗口中绘制出如图6所示的Hilbert曲线。这个图形可以看成是图5向左旋转90°得到的。实际上，由图2可知，将方式（一）的图形向左旋转90°得到的就是方式（二）的图形。
图6 调用Two(depth)时绘制的图形
将程序中调用语句“One(depth)”改写成“Three(depth)”，同时修改初始坐标为
“var x = 450-h; var y = 450-h;”，则在浏览器窗口中绘制出如图7所示的Hilbert曲线。
图7 调用THree(depth)时绘制的图形
将程序中调用语句“One(depth)”改写成“Four(depth);”，同时修改初始坐标为
“var x = 450-h; var y = 450-h;”，则在浏览器窗口中绘制出如图8所示的Hilbert曲线。
图8 调用Four(depth)时绘制的图形
将Hilbert曲线的生成过程进行动画展示，编写如下的HTML代码。
<!DOCTYPE>
<html>
<head>
<title>Hilbert曲线</title>
</head>
<body>
<canvas id="myCanvas" width="500" height="500" style="border:3px double #996633;"></canvas>
<script type="text/javascript">
var canvas = document.getElementById('myCanvas');
var ctx = canvas.getContext('2d');
var depth=1;
function drawShapes(n,s,x1,y1,x2,y2)
{
dx = x2 - x1,
dy = y2 - y1;
if (n>1)
{
if(s>0)
{
drawShapes(n-1,-1,x1,y1,(x1+x2)/2,(y1+y2)/2);
drawShapes(n-1,1,x1,(y1+y2)/2,(x1+x2)/2,y2);
drawShapes(n-1,1,(x1+x2)/2,(y1+y2)/2,x2,y2);
drawShapes(n-1,-1,x2,(y1+y2)/2,(x1+x2)/2,y1);
}
else
{
drawShapes(n-1,1,x1,y1,(x1+x2)/2,(y1+y2)/2);
drawShapes(n-1,-1,(x1+x2)/2,y1,x2,(y1+y2)/2);
drawShapes(n-1,-1,(x1+x2)/2,(y1+y2)/2,x2,y2);
drawShapes(n-1,1,(x1+x2)/2,y2,x1,(y1+y2)/2);
}
}
if (n==1)
{
ctx.lineTo(x1+dx/4,y1+dy/4);
ctx.lineTo(x1+(2-s)*dx/4, y1+(2+s)*dy/4);
ctx.lineTo(x1+3*dx/4, y1+3*dy/4);
ctx.lineTo(x1+(2+s)*dx/4,y1+(2-s)*dy/4);
}
}
function go()
{
ctx.clearRect(0,0,canvas.width,canvas.height);
ctx.lineWidth = 2;
ctx.strokeStyle = "red";
ctx.beginPath();
ctx.moveTo(50+400/Math.pow(2,depth+1),50+400/Math.pow(2,depth+1));
drawShapes(depth,1,50,50,450,450);
ctx.stroke();
depth++;
if (depth>6)
{
depth=1;
}
}
window.setInterval('go()', 1000);
</script>
</body>
</html>
在浏览器中打开包含这段HTML代码的html文件，可以看到在浏览器窗口中呈现出如图9所示的Hilbert曲线动态生成效果。
图9 Hilbert曲线动态生成
JavaScript图形实例：Hilbert曲线的更多相关文章
- JavaScript图形实例：线段构图
在“JavaScript图形实例:四瓣花型图案”和“JavaScript图形实例:蝴蝶结图案”中,我们绘制图形时,主要采用的方法是先根据给定的曲线参数方程计算出两点坐标,然后将两点用线段连接起来,线段 ...
- JavaScript动画实例：曲线的绘制
在“JavaScript图形实例:曲线方程”一文中,我们给出了15个曲线方程绘制图形的实例.这些曲线都是根据其曲线方程,在[0,2π]区间取一系列角度值,根据给定角度值计算对应的各点坐标,然后在计算出 ...
- JavaScript图形实例：再谈IFS生成图形
在“JavaScript图形实例:迭代函数系统生成图形”一文中,我们介绍了采用迭代函数系统(Iterated Function System,IFS)创建分形图案的一些实例.在该文中,仿射变换函数W的 ...
- JavaScript图形实例：随机SierPinski三角形
在“JavaScript图形实例:SierPinski三角形”中,我们介绍了SierPinski三角形的基本绘制方法,在“JavaScript图形实例:迭代函数系统生成图形”一文中,介绍了采用IFS方 ...
- JavaScript图形实例：Koch曲线
Koch曲线的构造过程是:取一条长度为L0的直线段,将其三等分,保留两端的线段,将中间的一段改换成夹角为60度的两个等长直线:再将长度为L0/3的4个直线段分别进行三等分,并将它们中间的一段均改换成夹 ...
- JavaScript图形实例：四瓣花型图案
设有坐标计算公式如下: X=L*(1+SIN(4α))*COS(α) Y=L*(1+SIN(4α))*SIN(α) 用循环依次取α值为0~2π,计算出X和Y,在canvas画布中对坐标位置(X,Y)描 ...
- JavaScript图形实例：图形的旋转变换
旋转变换:图形上的各点绕一固定点沿圆周路径作转动称为旋转变换.可用旋转角表示旋转量的大小. 旋转变换通常约定以逆时针方向为正方向.最简单的旋转变换是以坐标原点(0,0)为旋转中心,这时,平面上一点P( ...
- JavaScript图形实例：圆内螺线
数学中有各式各样富含诗意的曲线,螺旋线就是其中比较特别的一类.螺旋线这个名词来源于希腊文,它的原意是“旋卷”或“缠卷”.例如,平面螺旋线便是以一个固定点开始向外逐圈旋绕而形成的曲线. 阿基米德螺线和黄 ...
- JavaScript图形实例：正多边形
圆心位于坐标原点,半径为R的圆的参数方程为 X=R*COS(θ) Y=R*SIN(θ) 在圆上取N个等分点,将这N个点首尾连接N条边,可以得到一个正N边形. 1．正多边形阵列 构造一个8行8列的正N( ...
随机推荐
- java实现第四届蓝桥杯阶乘位数
阶乘位数 题目描述 如图p1.jpg所示,3 x 3 的格子中填写了一些整数. 我们沿着图中的红色线剪开,得到两个部分,每个部分的数字和都是60. 本题的要求就是请你编程判定:对给定的m x n 的格 ...
- TZOJ 复习时间
描述 为了能过个好年,xhd开始复习了,于是每天晚上背着书往教室跑.为了追求更高的效率,xhd要根据难度值来选择合适的课程进行复习,复习后一门课的效率为前一门课之间的难度差的平方,而复习第一门课的效率 ...
- 制作zipkin docker镜像
这里使用的zipkin知识基于内存的版本,没有接入外部存储 https://zipkin.io/ https://github.com/openzipkin/zipkin https://github ...
- Promise相关学习
what? Promise对象表示一个异步操作的最终状态(完成或失败),以及其返回的值 https://developer.mozilla.org/zh-CN/docs/Web/JavaScript/ ...
- 【百度前端技术学院 Day7/8】布局
1. 定位 1.1 文档流 单个元素: 块级元素:内容宽度是其父元素的宽度的100%,并且与其内容一样高. 内联(行内)元素:高宽与他们的内容高宽一样.(所以不能为他们设置宽高) 元素之间的交互: 块 ...
- URL 链接中的 UTM参数何定义？
浏览网页或者点击广告的时候,细心的朋友们或者有关注浏览器地址栏的 URL 链接时,一定会发现 utm_source 或者与其类似的链接,那么链接中的这个UTM参数有什么用呢? UTM 为“Urchin ...
- pip install 执行过程中遇到的各种问题
一.pip install 安装指定版本的包 要用 pip 安装指定版本的 Python 包,只需通过 == 操作符 指定. pip install robotframework == 2.8.7 将 ...
- ojdbc6中OraclePreparedStatement的ArrayIndexOutOfBoundsException异常BUG-6396242
现场信息 Caused by: java.lang.ArrayIndexOutOfBoundsException: -32203 at oracle.jdbc.driver.OraclePrepare ...
- TensorFlow从0到1之浅谈感知机与神经网络（18）
最近十年以来,神经网络一直处于机器学习研究和应用的前沿.深度神经网络(DNN).迁移学习以及计算高效的图形处理器(GPU)的普及使得图像识别.语音识别甚至文本生成领域取得了重大进展. 神经网络受人类大 ...
- 这一次搞懂Spring事务是如何传播的
文章目录 前言 正文 事务切面的调用过程 事务的传播性概念 实例分析 总结 前言 上一篇分析了事务注解的解析过程,本质上是将事务封装为切面加入到AOP的执行链中,因此会调用到MethodIncepto ...