The best Fibonacci is achieved in js

The best Fibonacci is achieved in js

the best realized by using js 斐波那契数列

"use strict";

/**
 *
 * @author xgqfrms
 * @license MIT
 * @copyright xgqfrms
 * @created 2020-12-10
 * @modified
 *
 * @description
 * @description
 * @difficulty Easy Medium Hard
 * @complexity O(n)
 * @time O(n)
 * @augments
 * @example
 * @link
 * @solutions
 *
 * @best_solutions
 *
 */

const log = console.log;

//   good O(2*n)
function fibonacci(num, memo) {
  memo = memo || {};
  if (memo[num]) {
    return memo[num];
  }
  if (num <= 1) {
    return 1;
  }
  return memo[num] = fibonacci(num - 1, memo) + fibonacci(num - 2, memo);
}

//   bad O(2^n), 卡死了
function fib(n) {
  // 1, 1, 2, 3, 5, 8...n, (n - 1) + (n - 2)
  if(n <= 2) {
    return 1;
  } else {
    // n >= 3
    return fib(n - 1) + fib(n - 2);
  }
}

function f(num, memo) {
  memo = memo || {};
  if (memo[num]) {
    return memo[num];
  }
  if (num <= 2) {
    return 1;
  }
  // RangeError: Maximum call stack size exceeded ？？？
  return memo[num] = f(num - 1, memo) + f(num - 2, memo);
}

function sumOddFibonacciNumbers(num) {
  //  write code here.
  let result = 0;
  for (let i = 1; i <= num; i++) {
    const temp = f(i);
    // const temp = fibonacci(i);
    // const temp = fib(i);
    if(temp <= num && (temp % 2) !== 0) {
      // odd
      result += temp;
      // log(`temp =`, temp)；
    }
  }
  return result;
}

const test1 = sumOddFibonacciNumbers(10);
// 10
const test2 = sumOddFibonacciNumbers(1000);
// 1785
// const test3 = sumOddFibonacciNumbers(4000000);
// 4613732

log(`\ntest =`,  test1, test1 === 10 ? `` : ``);
log(`\ntest =`,  test2, test2 === 1785 ? `` : ``);
// log(`\ntest =`,  test3, test3 === 4613732 ? `` : ``);

// RangeError: Maximum call stack size exceeded ？？？

bug

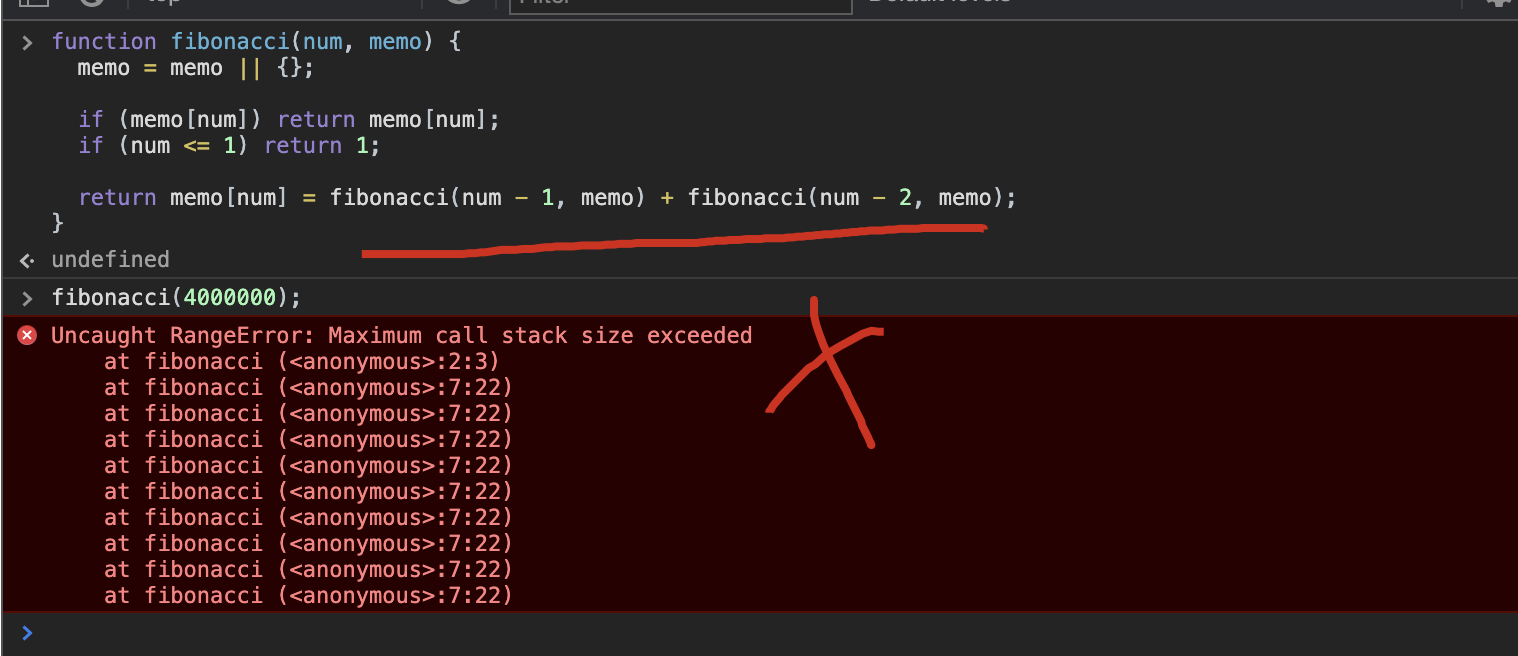
function fibonacci(num, memo) {
  memo = memo || {};

  if (memo[num]) return memo[num];
  if (num <= 1) return 1;

  return memo[num] = fibonacci(num - 1, memo) + fibonacci(num - 2, memo);
}

fibonacci(4000000);

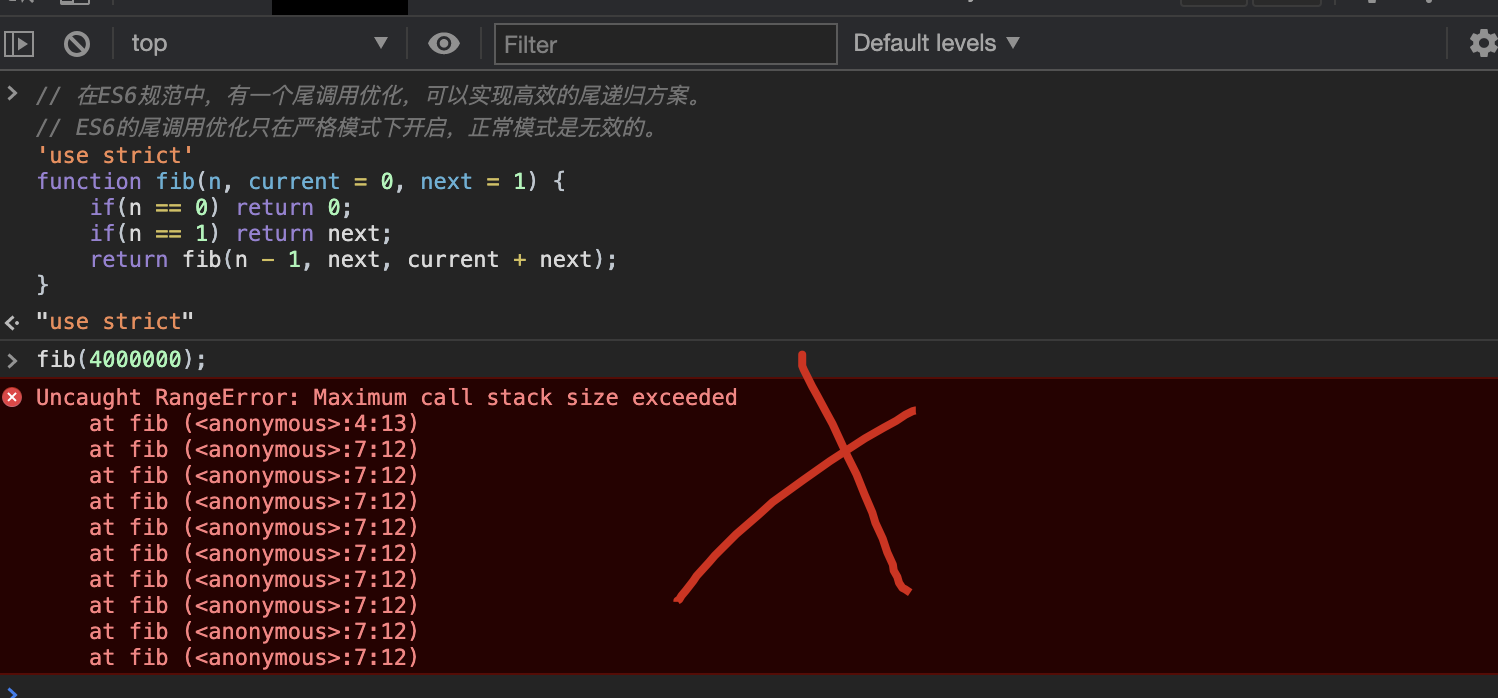
// 在 ES6 规范中，有一个尾调用优化，可以实现高效的尾递归方案。
// ES6 的尾调用优化只在严格模式下开启，正常模式是无效的。
'use strict'
function fib(n, current = 0, next = 1) {
    if(n == 0) return 0;
    if(n == 1) return next;
    return fib(n - 1, next, current + next);
}

fib(4000000);
// Uncaught RangeError: Maximum call stack size exceeded

refs

https://www.cnblogs.com/xgqfrms/p/12909516.html

https://www.cnblogs.com/xgqfrms/archive/2004/01/13/12909516.html

https://scrimba.com/learn/adventcalendar/-javascript-challenge-sum-odd-fibonacci-numbers-introduction-cmpWaRcW

---

---

xgqfrms 2012-2020

www.cnblogs.com 发布文章使用：只允许注册用户才可以访问！

---