itest(爱测试) 开源一站式敏捷测试管理平台&极简项目管理,重大升级(接口测试)6.0.0 发布

itest 简介

itest 开源敏捷测试管理，testOps 践行者，极简的任务管理，测试管理，缺陷管理，测试环境管理，接口测试5合1，又有丰富的统计分析。可按测试包分配测试用例执行，也可建测试迭代(含任务，测试包，BUG)来组织测试工作，也有测试环境管理，还有很常用的测试度量；对于发版频繁，需求常变，itest还可导出用例，线下修改、执行，新增后再导入（同步）到线上；且可根据测试策略来设置测试流程，并可实时调整；在测试看板中，能查看迭代报告，测试包执行情况，测试任务进展，也可以在看板上直接执行用包用例。6.0.0中增加的接口测试简单易用，对测试人友好。

官网http://www.itest.work

在线体验1  http://www.itest.work/demo

在线体验2  http://120.78.0.137/demo

v6.0.0 下载地址 ：itest下载

  先庆祝一下itest 入选tid  2020 IT研发管理工具选型手册。

待接口测试几轮迭代，相对完善后，就着手和CD/CI 打通的集成实现

6.0.0 详情如下:

原计划是7月10日6.0.0发版本等。公司的工作一直忙，只有业余有时间维护，所以拖到了8月中旬，接口测试功能下面一睹为快。

（一）接口测试 功能概览：

         基本流程： (1)BaseUrl 设置------>(2)基础认证设置 ----->（3）维护接口用例----->(4)建接口测试场景(可在迭代中直接增加)--->(5)手动执行接口测试场景(可单个，也可一键执行场景中所有接口)或定时执行测试场景。

       1:接口测试总览

  2:全局设置

3:接口用例维护

接口参数维护，非常方便  ，对测试人员友好

 

 4：接口场景

在场景中可单个，也可一键执行所有接口用例，也可手动调整执行顺序

 5:接口执行日志

 6:定时执行接口测试场景

     

6.1.0 将于 8月底发部，支持对响应结果断言，且不用测试人员写代码，如拖拉操作生成jsonpath ，省得测试人员再去学jsonpath 。拖拉效率高.如下几图所示:

 

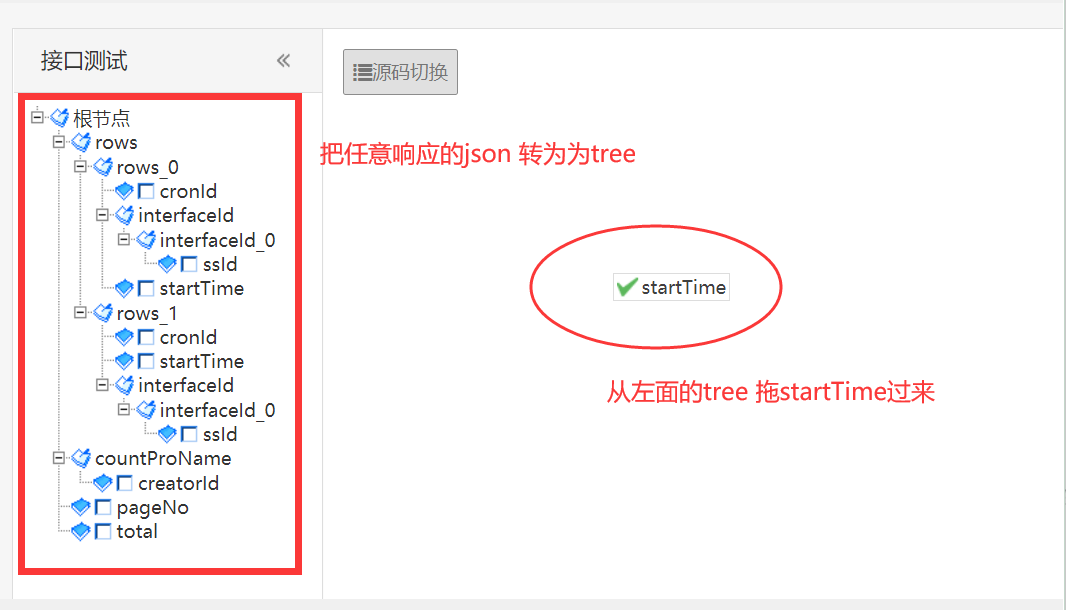
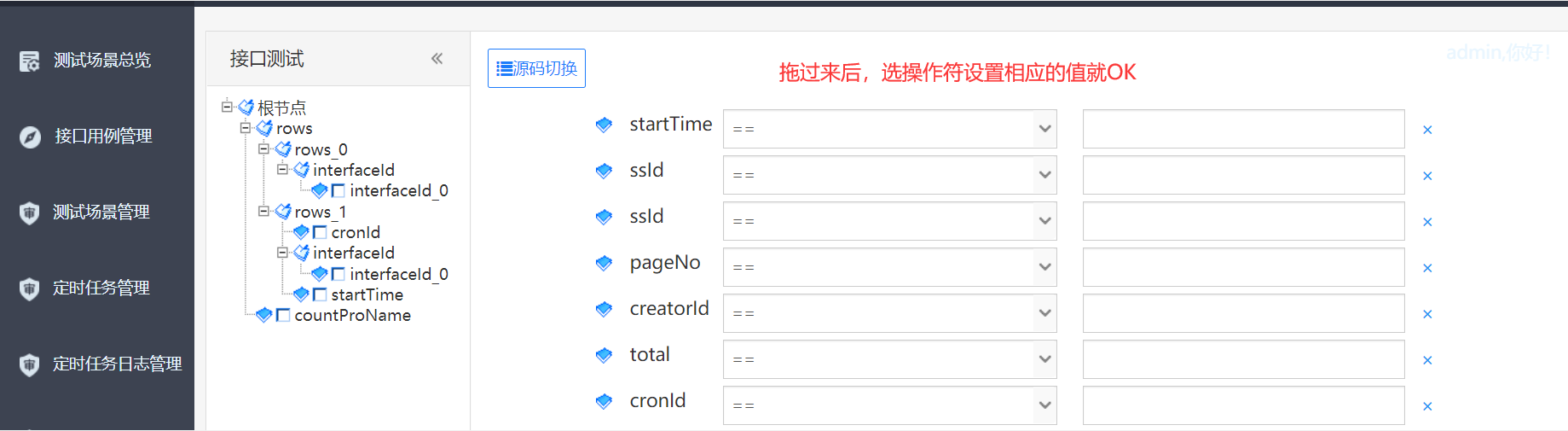
 以上是实现接口测试的首个版本，8月底发6.1.0 支持断言后，下下版本将支持mock 和通过文档生成mock 及接口用例。

(二)产品截图及功能概览

功能模型及引导图

引导图上蓝色文字是热点，可以点击，方便引导上手

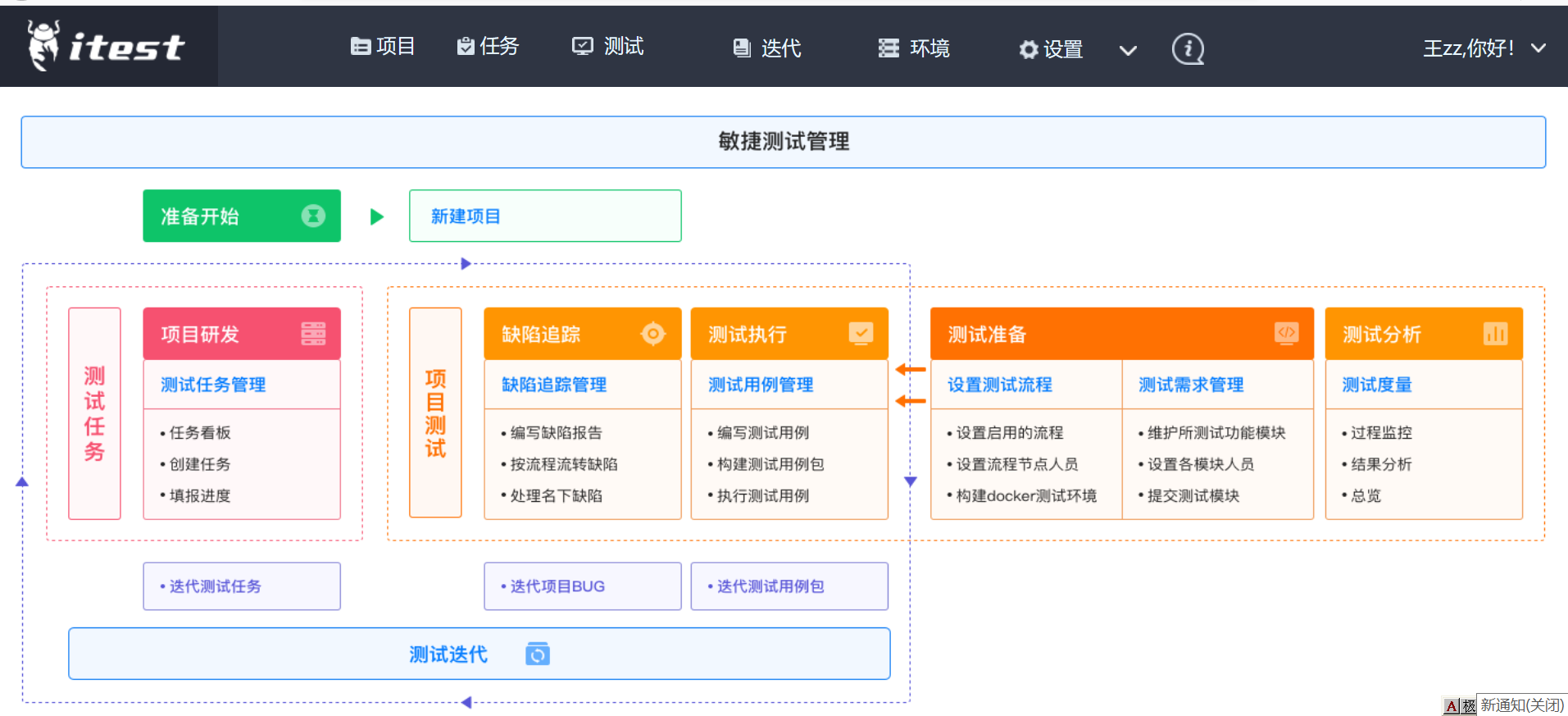
可线下离线处理测试用例，再同步到线上，

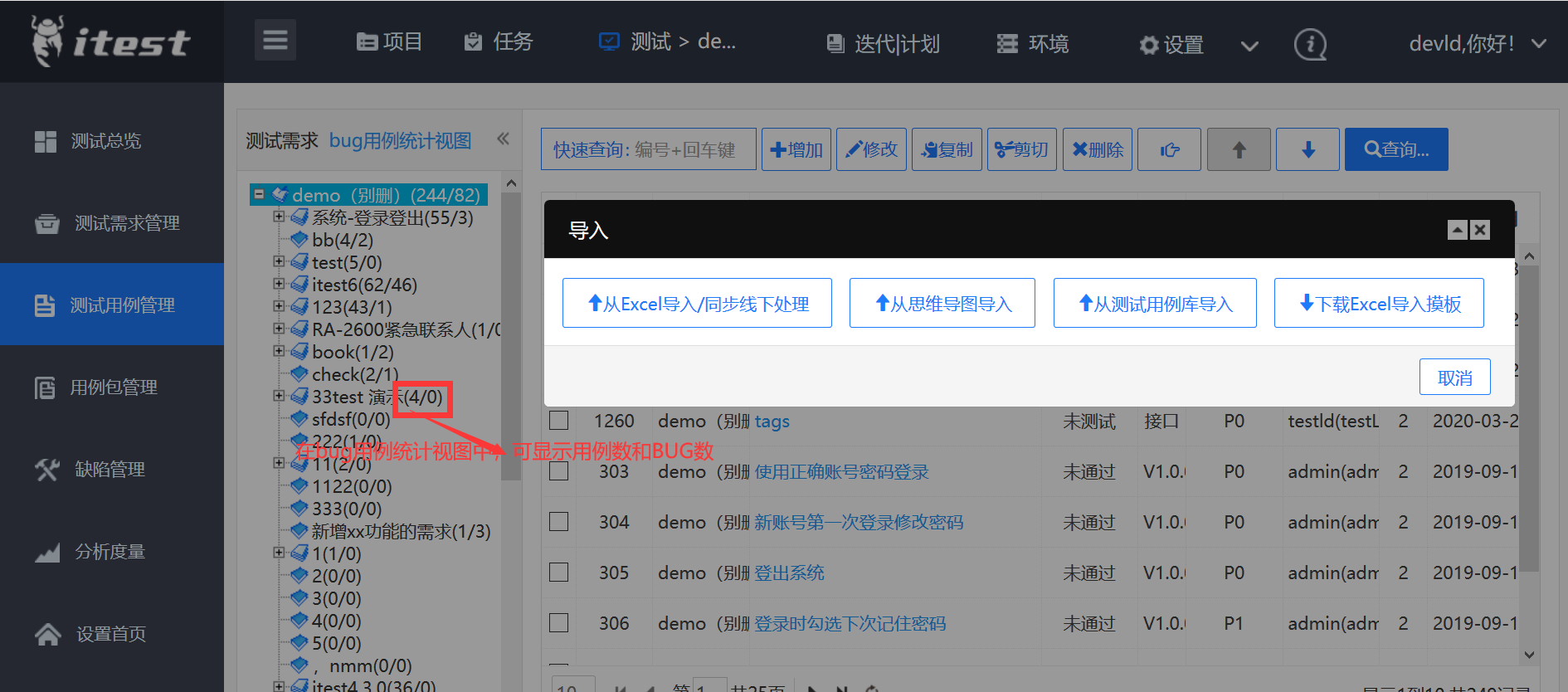
除了可同步线下执行，还支持多种导入，在用例BUG统计示图中，测试需求分解对上，

每个模块上显示BUG数和用例数

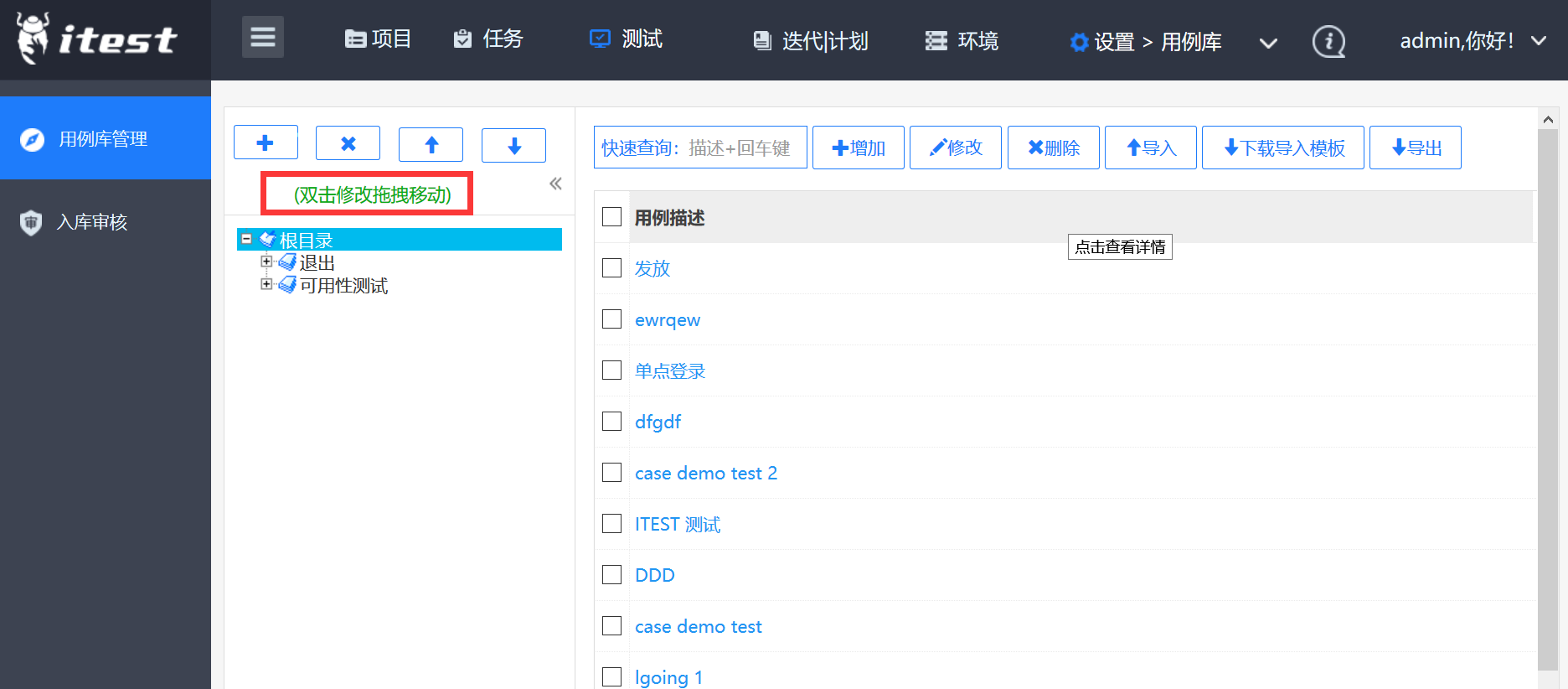
用例库维护公共用例，在项目中可以从用例库或是EXCEL呀是xmind 中导入用例,且在导入时，如需求项，用例分类，优先级，以及用例标签 ，如系统中不存在，会自动在导入时建立

可按测试包分配测试任务，通过把多个测试包加到测试迭代中，统计测试执行情况

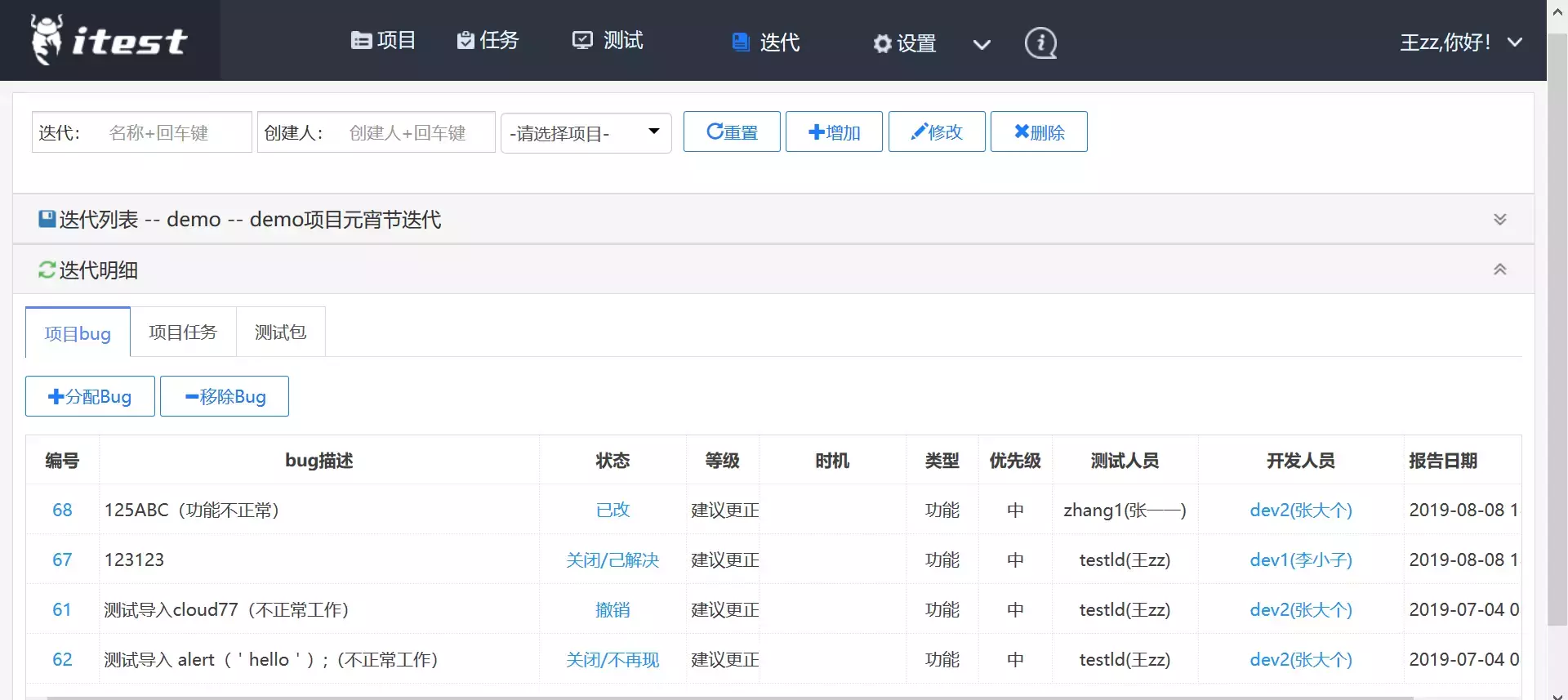
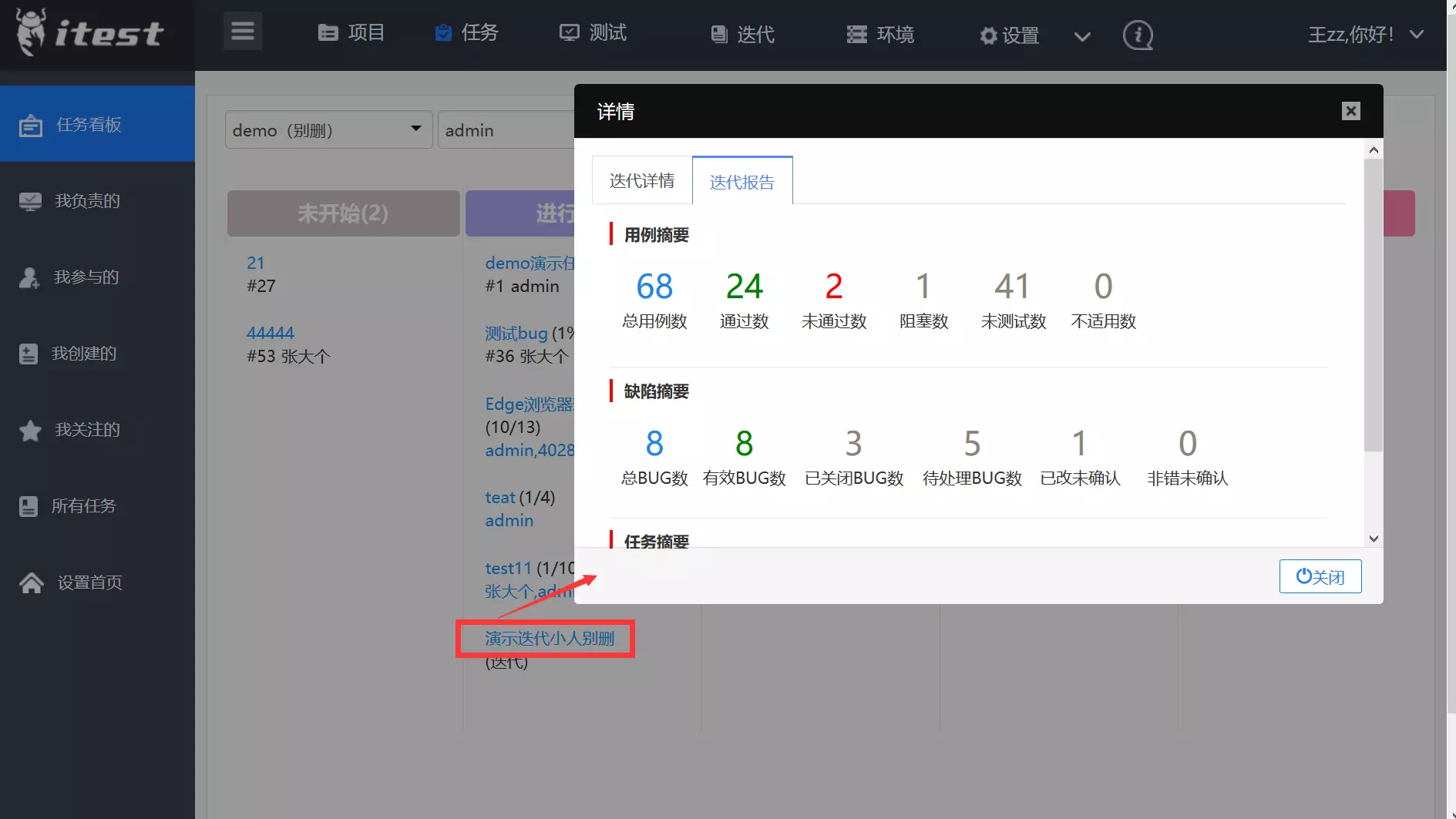
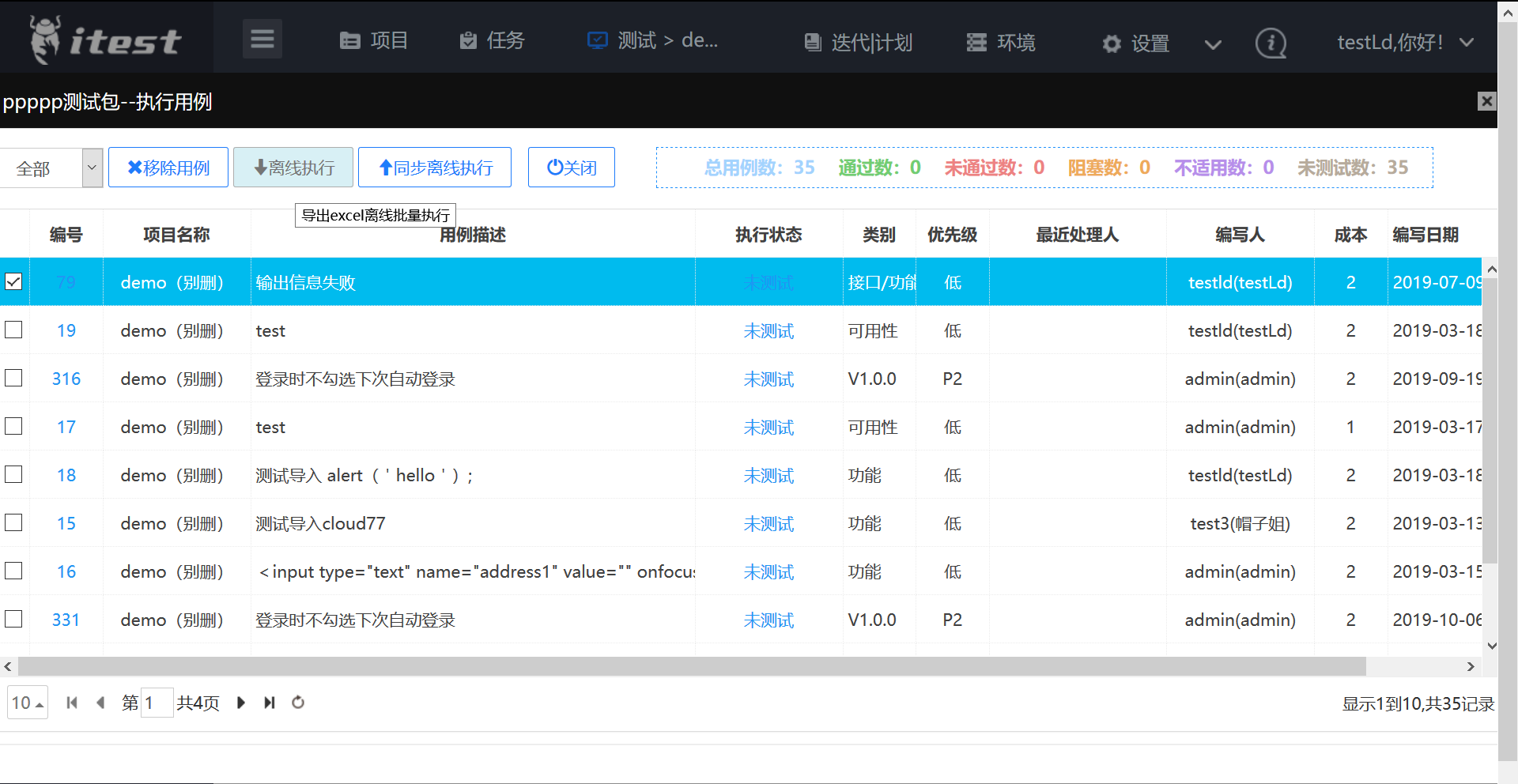
执行测试用例包任务

可在看板上，填写任务进度，执行测试用例包，或是处理流转到名下的BUG

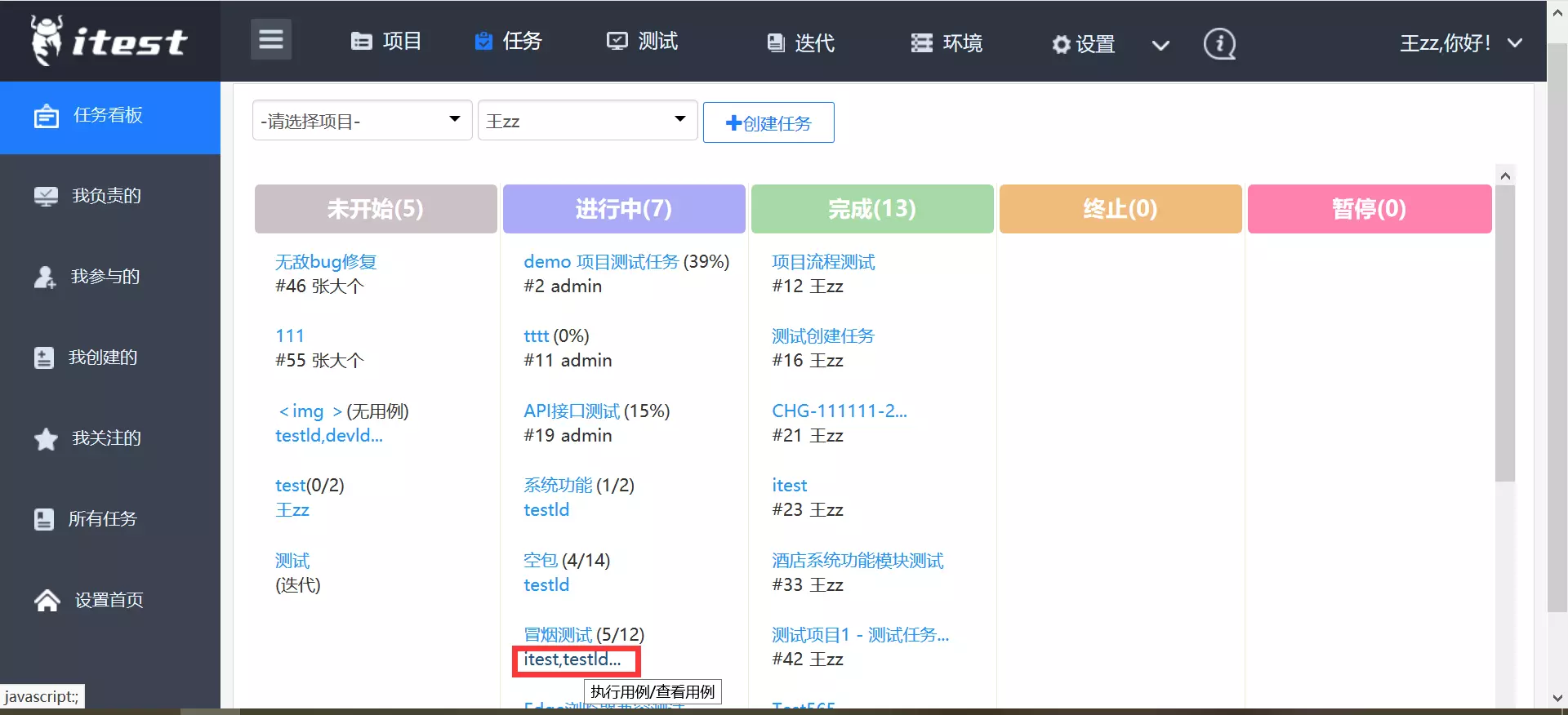
在看板上，直接可以执行用例

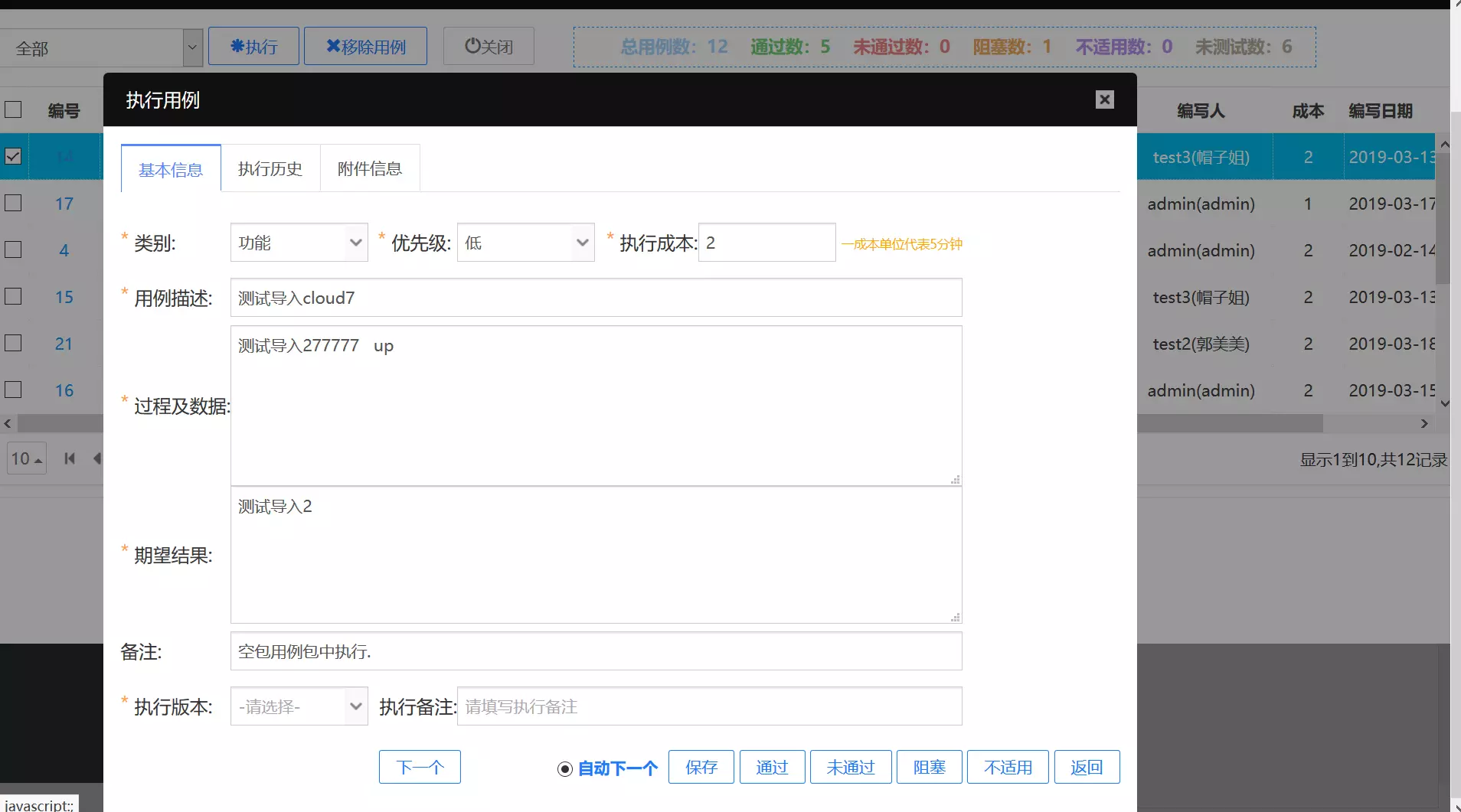
流程驱动测试

流程驱动缺陷在26种状态中演化，更精准反正工作实况

测试流程引擎自动推算可演化状态及流转到谁名下，且可实时调整流程

从 BUG的邮件通知中连BUG链接，可能直接处理BUG

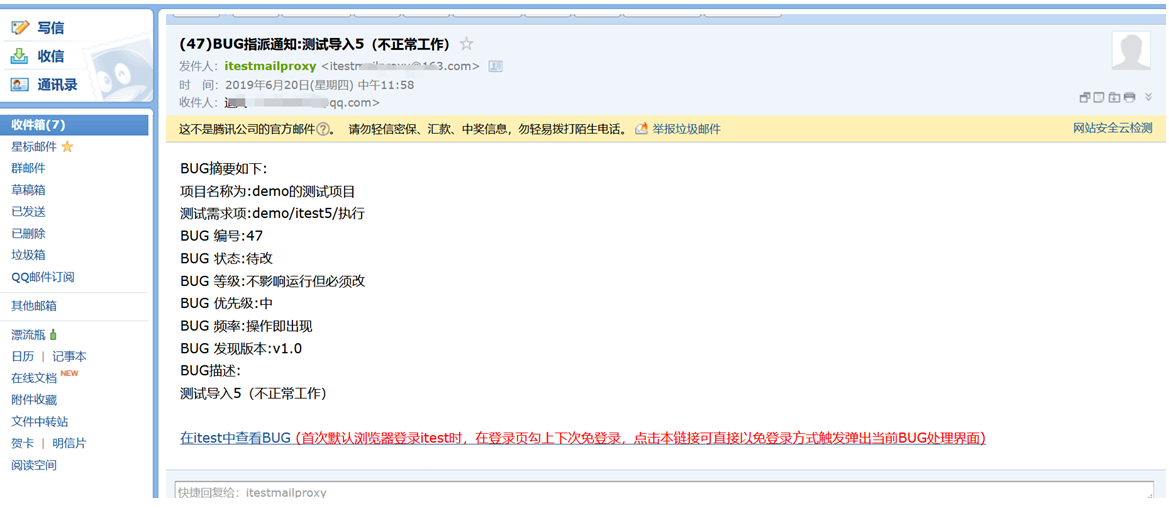
在收到的BUG邮件中，带一个连接，一点就自动登录ITEST，同时，弹出邮件中的BUG处理界面

多维度测试度量

趋势分析洞察研发过程潜在风险，为项目管控提供决策依据

结果数据分析掌控团队效率，为持续改进提供量化数据支持

测试总揽，测试经理每日工作复盘好帮手，量化的测试日报

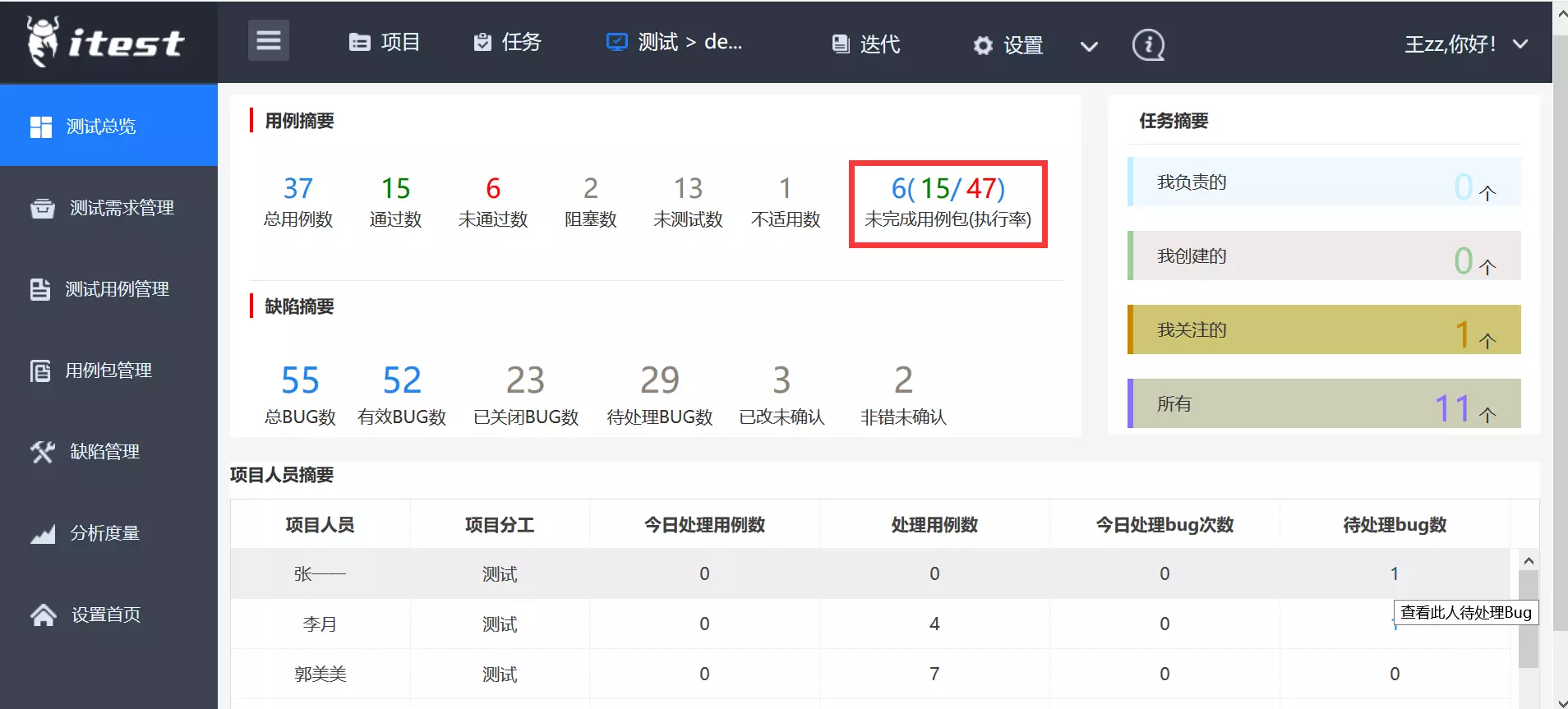
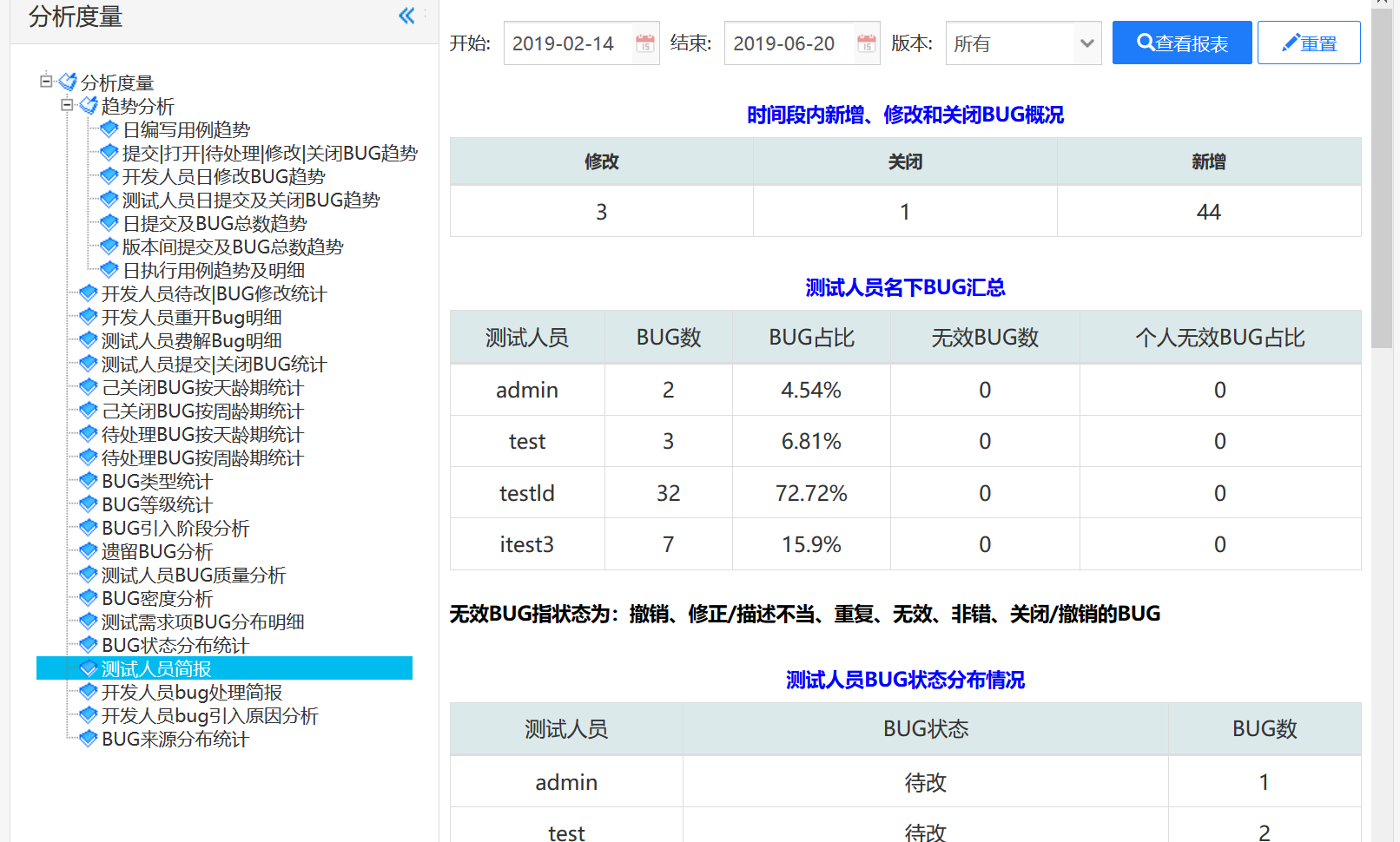
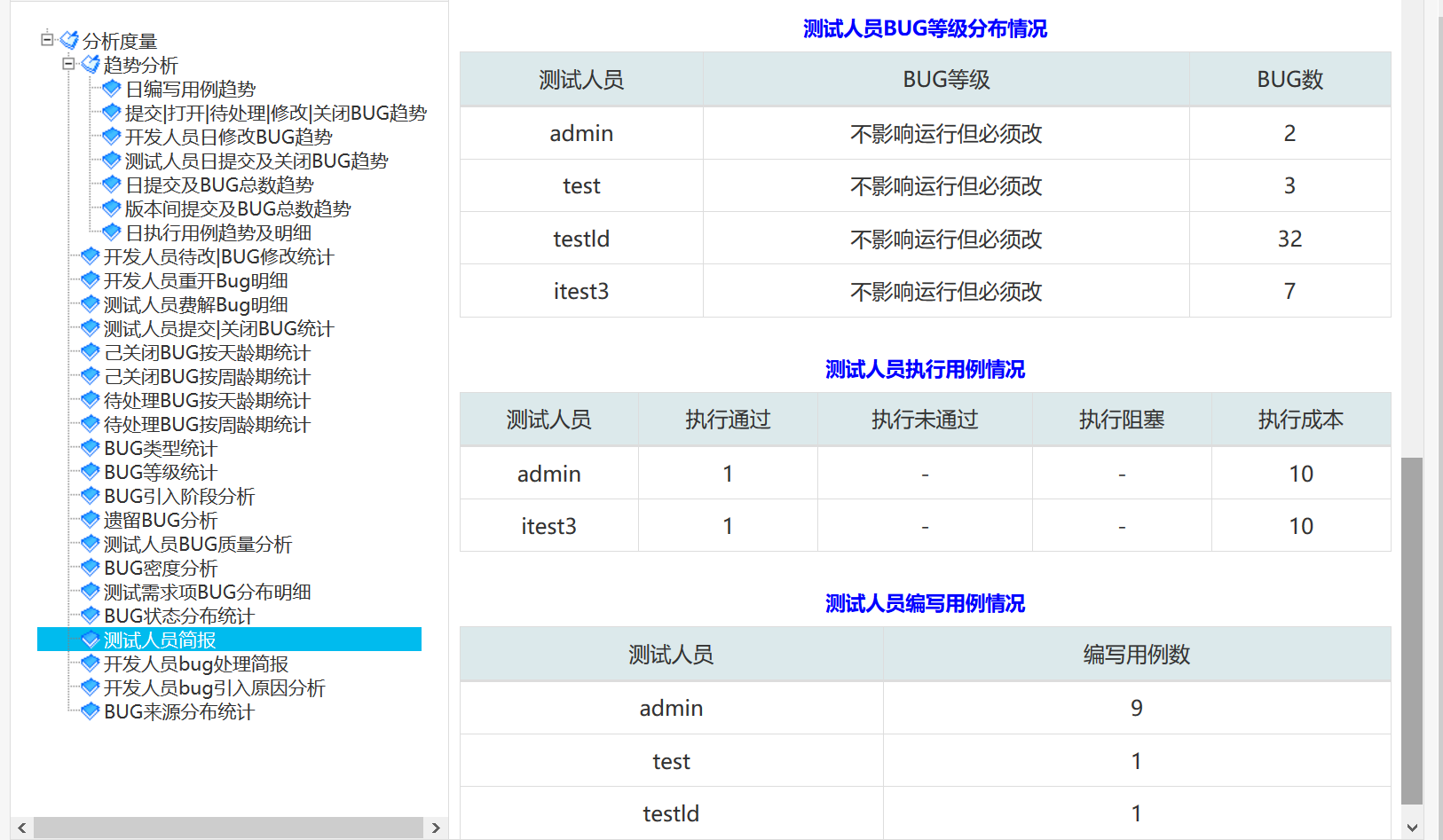
测试人员简报： 里面有测试人员写用例情况，执行用例情况，提交的 BUG数，提交的BUG 按

状态按人分布，提交的BUG按类型按人分布，提交的BUG按等级按人分布，且可按不同版本作

为条件进行分析

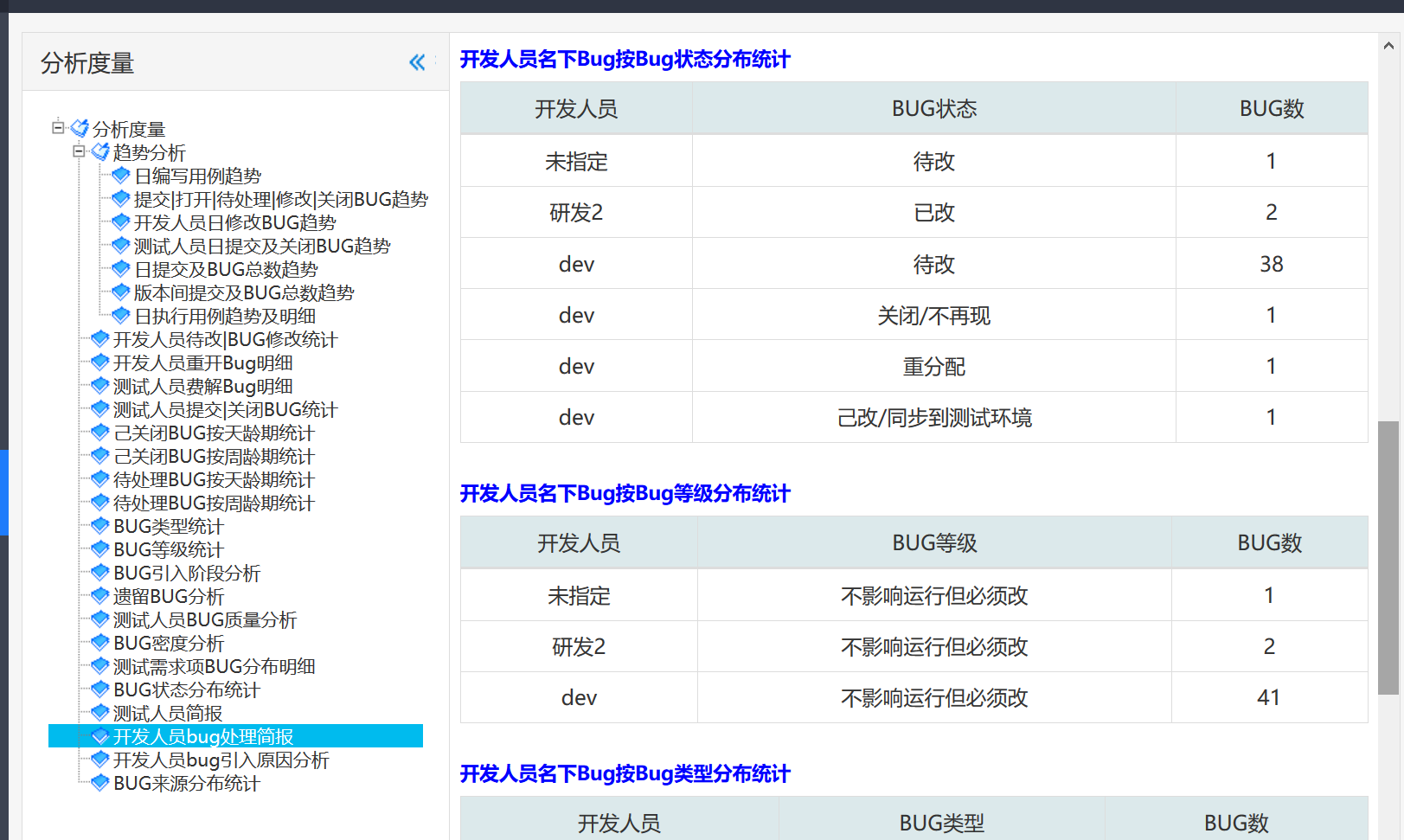
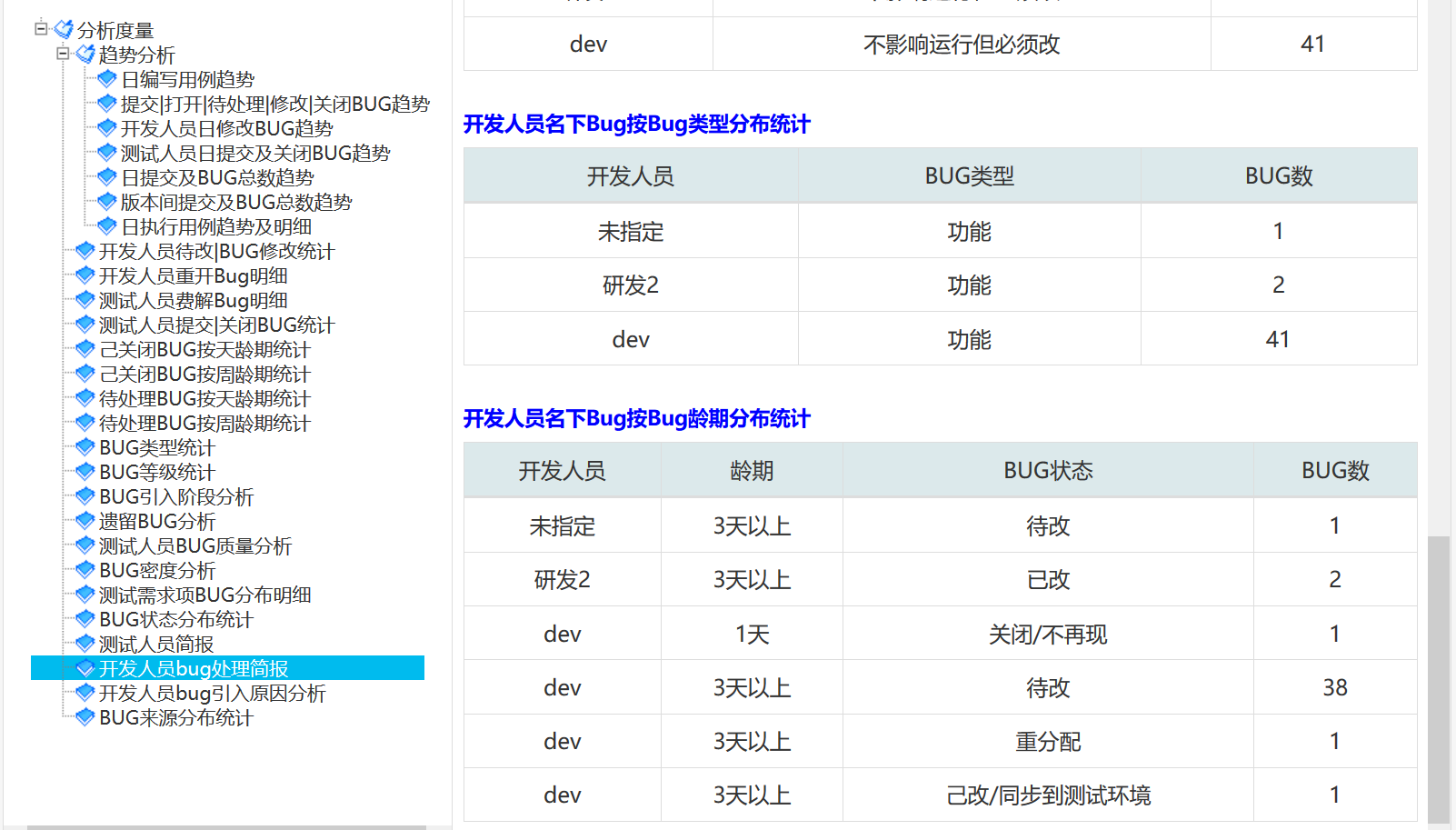
开发人员处得BUG简报 ： 有开发人员BUG数统计， 也有按bug状态按人分布，按bug等级按人分布，

按bug类型按人分布,按人按BUG 龄期分布(龄期可按天也可按周计)，且可按不同版本作为条件进行分析

测试环境维护