Codeforces Edu Round 48 A-D

A. Death Note

简单模拟，可用\(\%\)和 \(/\)来减少代码量

#include <iostream>
#include <cstdio>
using namespace std;
const int N = 200010;
int n, m, a[N], cnt = 0, tot = 0;
int main(){
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i++){
        scanf("%d", a + i);
        cnt = (tot + a[i]) / m;
        tot = (tot + a[i]) % m;
        printf("%d ", cnt);
    }
}

B - Segment Occurrences

预处理\(A、B\)的\(Hash\)表，可以将时间复杂度降到\(O(qn)\)

#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;
typedef unsigned long long ULL;
const int N = 1010, B = 221;
int n, m, q, len;
char s[N], t[N];
ULL P[N], S[2][N];
ULL inline get(int l, int r, int c){
    return S[c][r] - S[c][l - 1] * P[r - l + 1];
}
int main(){
    scanf("%d%d%d%s%s", &n, &m, &q, s + 1, t + 1);
    P[0] = 1;
    for(int i = 1; i <= n; i++){
        P[i] = P[i - 1] * B;
        S[0][i] = S[0][i - 1] * B + s[i];
        S[1][i] = S[1][i - 1] * B + t[i];
    }
    while(q--){
        int l, r, res = 0; scanf("%d%d", &l, &r);
        for(int i = l; i <= r - m + 1; i++)
            if(get(i, i + m - 1, 0) == get(1, m, 1))res++;
        printf("%d\n", res);
    }
    return 0;
}

C - Vasya And The Mushrooms

硬核模拟 + 前缀和处理。要不重复的绕完 \(2 * N\) 的格子，从左上角出发，要么\(S\)形绕几次然后绕大圈，要么绕整个的一圈。

可以枚举绕\(S\)格子的次数，\(S\)的部分可以前缀和计算，系数是一样的，后面的部分计算比较复杂。

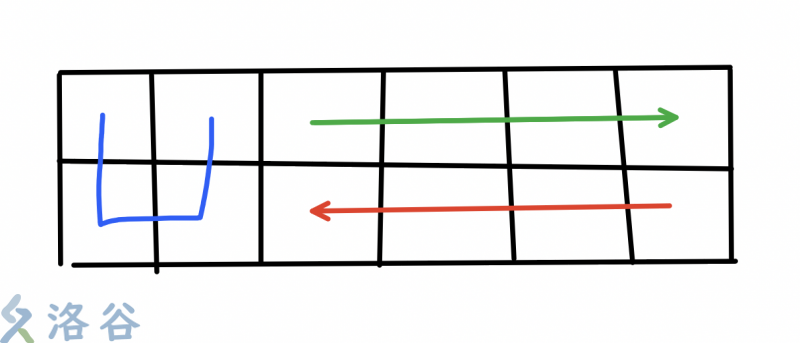
第一种情况，前面的部分绕了了几个完整的 \(U\)。要从上方出发。

求（\(now\)代表\(U\)字结束（包括）的列数）：

上半部分：$\sum_{i=now + 1}^n a[0][i] * (i * 2) $

我们发现，数列后缀和的后缀和是：

\(sufx[j] = \sum_{i = j} ^ n a[i] * (i - j + 1) = a[j] * 1 + a[j + 1] * 2 + … + a[n] * (n - j + 1)\)

故，把\(sufx[now + 1]\)再加上\(\sum_{i = j} ^ n a[i] * (i * 2 - 1)\)，即为答案，后面这部分可用后缀和\(O(1)\)计算。

下半部分：$\sum_{i=now + 1}^n a[1][i] * (n + (n - i + 1)) $

我们想要这样的东西：

\(a[i] * 3 + a[i + 1] * 2 + a[i + 2] * 1\)

这个看上去很像\(Hash\)表的原理，只不过\(b = 1\)，可以用hash表的思想在\(O(1)\) 求出这个，然后在用后缀和加上系数既可。

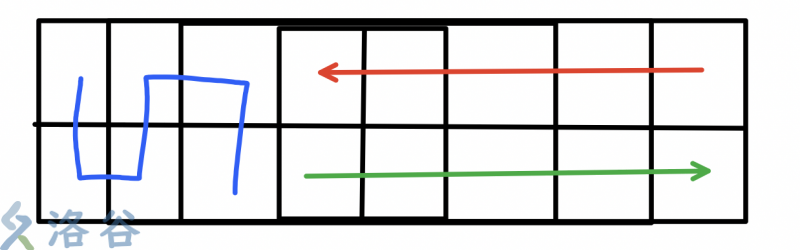
对于第二种情况，只不过将上下颠倒，我们互换一下处理方式既可。

预处理前缀和、后缀和和枚举\(S\)的时间都为\(O(n)\)，每次求解只需\(O(1)\)，故总共复杂度为$ O(n) $的

#include <cstdio>
#include <iostream>
#include <cmath>

using namespace std;
typedef long long LL;
const int N = 300010;
//s形的预处理
int n, a[2][N];
LL pre[2][N], s[2][N], suf[2][N], sum[N], prex[2][N], sufx[2][N], ans = -1;

int main(){
    scanf("%d", &n);
    for(int i = 1; i <= n; i++) scanf("%d", &a[0][i]);
    for(int i = 1; i <= n; i++) scanf("%d", &a[1][i]);
    int S = n >> 1, tot = 0;
    for(int i = 1; i <= S * 2; i+=2){
        s[0][i] = (LL)a[0][i] * (tot++); s[1][i] = (LL)a[1][i] * (tot++);
        s[1][i + 1] = (LL)a[1][i + 1] * (tot++); s[0][i + 1] = (LL)a[0][i + 1] * (tot++);
    }

    for(int i = 0; i < 2; i++)
        for(int j = 1; j <= n; j++){
            pre[i][j] = pre[i][j - 1] + a[i][j];
            prex[i][j] = prex[i][j - 1] + pre[i][j];
        }

    for(int j = 0; j < 2; j++)
        for(int i = n; i >= 1; i--){
            suf[j][i] = suf[j][i + 1] + a[j][i];
            sufx[j][i] = sufx[j][i + 1] + suf[j][i];
        }

    for(int i = 0; i <= n; i++){
        LL tot = sum[i] = sum[i - 1] + s[0][i] + s[1][i];
        //如果是奇数，则在下面出发
        if(i % 2){
            tot += (n + i - 1) * suf[0][i + 1] + (prex[0][n] - prex[0][i] - (n - i) * pre[0][i]);
            tot += (i * 2 - 1) * suf[1][i + 1]  + (sufx[1][i + 1]);
        }else{
            //从上面出发
            tot += (i * 2 - 1) * suf[0][i + 1] + (sufx[0][i + 1]);
            tot += (n + i - 1) * suf[1][i + 1] + (prex[1][n] - prex[1][i] - (n - i) * pre[1][i]);
        }
        ans = max(ans, tot);
    }

    printf("%lld", ans);
    return 0;
}

D - Vasya And The Matrix

参考题解。 存在性参考异或的性质，\(x\) \(xor\) $ x = 0$ 。

考虑构造一个合理的序列，只需将除了最后一行，最后一列的所有数添上\(0\)。

除右下角外其他数照搬数据，右下角用异或尝试既可。

#include <iostream>
#include <cstdio>
using namespace std;
const int N = 110;
int n, m, a[N], b[N], ans = 0;
int main(){
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i++) scanf("%d", a + i), ans ^= a[i];
    for(int i = 1; i <= m; i++) scanf("%d", b + i), ans ^= b[i];

    if(ans != 0)puts("NO");
    else{
        puts("YES");
        ans = b[m];
        for(int i = 1; i < n; i++){
            for(int j = 1; j < m; j++)
                printf("0 ");
            printf("%d\n", a[i]);
            ans ^= a[i];
        }
        b[m] = ans;
        for(int i = 1; i <= m; i++) printf("%d ", b[i]);
    }
    return 0;
}