Abbott的复仇（Abbott's Revenge）

题目：有一个最多包含9*9个交叉点的迷宫。输入起点、离开起点时的朝向和终点，求一条最短路（多解时任意输出一个即可）。

这个迷宫的特殊之处在于：进入一个交叉点的方向（用NEWS这4个字母分别表示北东西南，即上右左下）不同，允许出去的方向也不同。例如，12WLFNRER*表示交叉点（1, 2)(上数第1行，左数第2列）有3个路标（字符“＊＂ 只是结束标志）， 如果进入该交叉点时的朝向为W(即朝左）， 则可以左转（L)或者直行（F); 如果进入时朝向为N或者E则只能右转（R)，如下图：

 

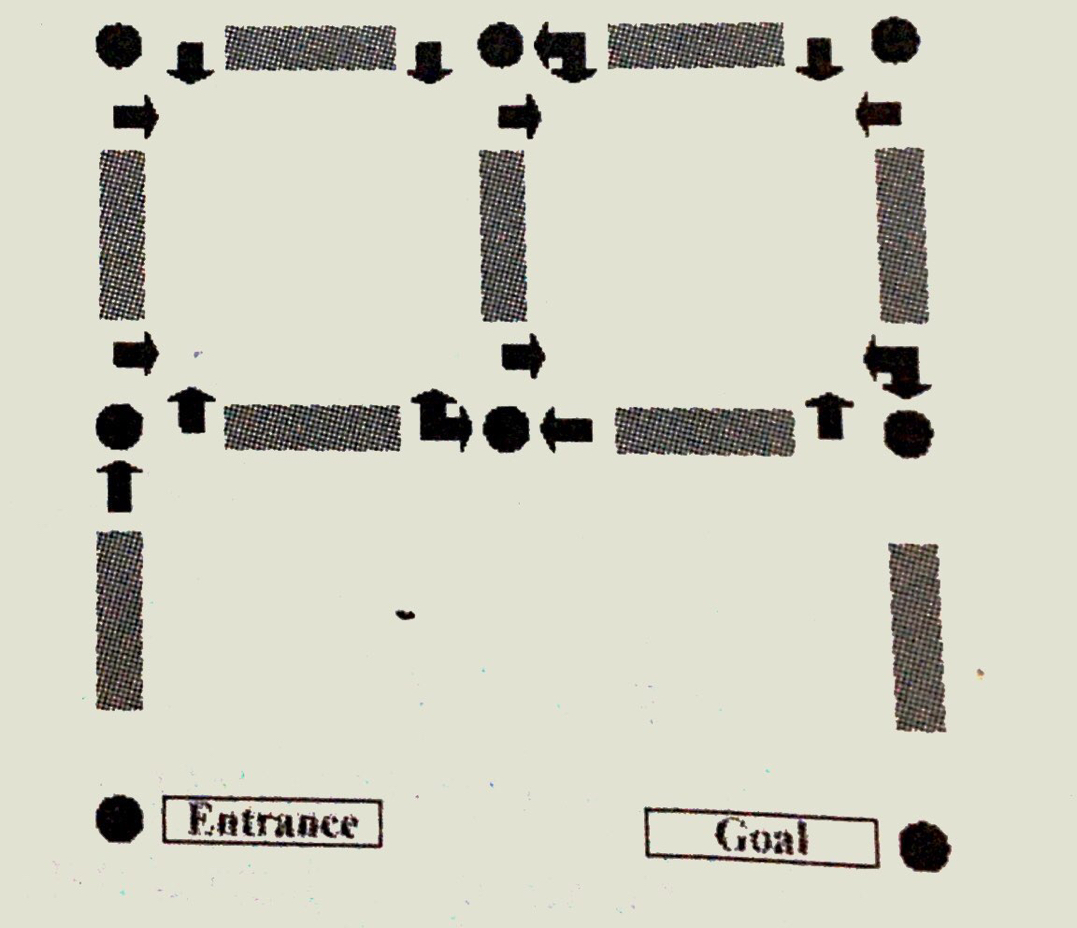
分析：此题直接做的话，略微有些困难，会BFS求最短路的知识铺垫会更容易理解一些，放上链接：BFS求最短路  了解的直接跳过。。。

这道题与普通的求最短路的题目的区别是每一个结点有各自的转向限制，因此在声明结构体的时候需要增加进入结点时的方向，则每个结点为（r,c,dir）,这样通过进入时的方向来判断可以往哪转向，而普通最短路四个方向都能转。另外初始状态是从入口朝着进入方向走一步之后的结点。其他思想与普通最短路一致，具体请参照代码，里边有注释。

 1 #include <iostream>
 2 #include <cstdio>
 3 #include <cmath>
 4 #include <cstring>
 5 #include <queue>
 6 #include <vector>
 7 using namespace std;
 8 const int maxn = 10;
 9 struct Node{
10     int r;
11     int c;
12     int dir;
13     Node(int r = 0,int c = 0,int dir = 0):r(r),c(c),dir(dir){}
14 };
15 int has_edg[maxn][maxn][4][3]; //每个结点的转向信息
16 int d[maxn][maxn][4];           //每个结点距离初始点的距离
17 Node pre[maxn][maxn][4];
18 int r0,c0,r1,c1,r2,c2,dir;
19 const char* dirs = "NESW";        //从上右下左四个方向进入（顺时针）
20 const char* turns = "FLR";        //直行、左拐、右拐四种转向
21 int dir_id(char d){    return strchr(dirs,d) - dirs;}
22 int turn_id(char t){ return strchr(turns,t) - dirs;}
23 int dr[4] = {-1,0,1,0};   //NESW四个方向
24 int dc[4] = {0,1,0,-1};
25 bool read_case(){
26     char s1[99],s2[99];
27     if(scanf("%d%d%s%d%d",&c0,&r0,s1,&r2,&c2) != 5) return false;
28
29     dir = dir_id(s1[0]); //从给出的起点走一步，获得起始位置
30     r1 = r0 + dr[dir];
31     c1 = c0 + dc[dir];
32
33     memset(has_edg,0,sizeof(has_edg));
34     for(;;){
35         int c,r;
36         cin >> c;
37         if(c == 0) break;
38         cin >> r;
39         while(scanf("%s",s2) == 1 && s2[0] != '*'){
40             for(int i = 1;i < strlen(s2);i++){
41                 has_edg[c][r][dir_id(s2[0])][turn_id(s2[i])] = 1;
42             }
43         }
44     }
45     return true;
46 }
47 Node walk(const Node& n,int turn){   //向前走一步
48     int dir = n.dir; //turn == 0时直走，方向不变
49     if(turn == 1) dir = (dir + 3) % 4; //左转(从进入时的方向顺时针数三个方向)
50     if(turn == 2) dir = (dir + 1) % 4; //右转(从进入时的方向顺时针数一个方向)
51     return Node(n.r + dr[dir],n.c + dc[dir],dir);
52 }
53 bool inside(int r,int c){
54     return r >= 1 && r <= 9 && c >= 1 && c <= 9;
55 }
56
57 void print_ans(Node n){
58     vector<Node> nodes;
59     for(;;){
60         nodes.push_back(n);
61         if(d[n.r][n.c][n.dir] == 0) break;
62         n = pre[n.r][n.c][n.dir];
63     }
64     nodes.push_back(Node(r0,c0,dir));
65     int cnt = 0;
66     for(int i = nodes.size();i >= 0;i--){
67         cout << "(" << nodes[i].r << "," << nodes[i].c << ")" << " ";
68         cnt++;
69         if(cnt % 10 == 0) cout << "\n";
70     }
71 }
72 void solve(){
73     queue<Node> q;
74     memset(d,-1,sizeof(d));
75     q.push(Node(r1,c1,dir));
76     d[r1][c1][dir] = 0; //初始点距离为0
77     while(!q.empty()){
78         Node n = q.front(); q.pop();
79         if(n.r == r2 && n.c == c2){ print_ans(n); return;}
80         for(int i = 0;i < 3;i++){
81             if(has_edg[n.r][n.c][n.dir][i]){
82                 Node v = walk(n,i);
83                 if(inside(v.r,v.c) && d[v.r][v.c][v.dir] == -1){
84                     d[v.r][v.c][v.dir] = d[n.r][n.c][n.dir] + 1;
85                     pre[v.r][v.c][v.dir] = n;
86                     q.push(v);
87                 }
88             }
89         }
90     }
91     printf("No Solution Possible\n");
92 }
93 int main(){
94     while(read_case()){
95         solve();
96     }
97     return 0;
98 }