二分法 (UVA10668 Expanding Rods)(二分+几何)

转载请注明出处：優YoU http://user.qzone.qq.com/289065406/blog/1301845324

大致题意：

一根两端固定在两面墙上的杆 受热弯曲后变弯曲。求前后两个状态的杆的中点位置的距离

解题思路：

几何和二分的混合体

　　　　　　　　　　　　　　

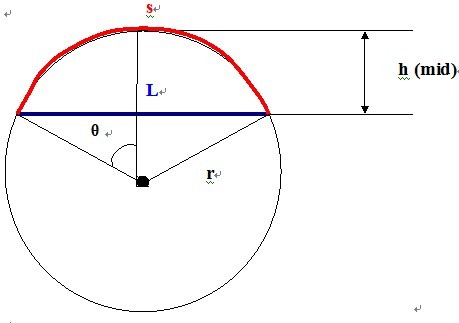
如图，蓝色为杆弯曲前，长度为L。红色为杆弯曲后，长度为s。h是所求

依题意知　　S=(1+n*C)*L

又从图中得到三条关系式;

　　（1）       角度→弧度公式  θr = 1/2*s

　　（2）       三角函数公式  sinθ= 1/2*L/r

　　（3）       勾股定理  r^2 – ( r – h)^2 = (1/2*L)^2

把四条关系式化简可以得到

　　　　　　　　

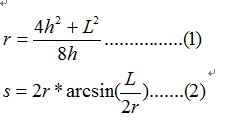
(1)逆向思维解二元方程组：

要求（1）式的h，唯有先求r；但是由于（2）式是三角函数式，直接求r比较困难

(2)因此要用顺向思维解方程组：

在h的值的范围内枚举h的值，计算出对应的r，判断这个r得到的(2)式的右边与左边的值S的大小关系 （ S= (1+n*C)*L ）

很显然的二分查找了。。。。。

那么问题只剩下 h 的范围是多少了

下界自然是0 (不弯曲)关键确定上界。题中提及到

Input data guarantee that no rod expands by more than one half of its original length.

意即输入的数据要保证没有一条杆能够延伸超过其初始长度的一半。就是说 S max = 3/2 L

理论上把上式代入（1）(2)方程组就能求到h的最小上界，但是实际操作很困难

因此这里可以做一个范围扩展，把h的上界扩展到 1/2L ，不难证明这个值必定大于h的最小上界，那么h的范围就为0<=h<1/2L

这样每次利用下界low和上界high就能得到中间值mid，寻找最优的mid使得(2)式左右两边差值在精度范围之内，那么这个mid就是h

精度问题是必须注意的

由于数据都是double，当low无限接近high时， 若二分查找的条件为while(low<high)，会很容易陷入死循环，或者在得到要求的精度前就输出了不理想的“最优mid”;

精度的处理方法只需将循环条件变为while(high - low < esp){...} ;其中 esp = 1e-6;

 #include <iostream>
 #include <sstream>
 #include <cstdio>
 #include <cstring>
 #include <cmath>
 #include <string>
 #include <vector>
 #include <set>
 #include <cctype>
 #include <algorithm>
 #include <cmath>
 #include <deque>
 #include <queue>
 #include <map>
 #include <stack>
 #include <list>
 #include <iomanip>
 using namespace std;
 ///
 #define PI acos(-1.0)
 #define INF 0xffffff7
 #define esp 1e-6
 #define maxn 250000 + 10
 typedef long long ll;
 ///
 int a[maxn];
 int main()
 {
     double l, n, c;
     while(scanf("%lf%lf%lf", &l, &n, &c) && l >=  && n >=  && c >= )
     {
         double s = (1.0 + n * c) * l;
         double high = 0.5*l;
         double low = 0.0;
         while(high - low > esp)
         {
             double m = (high + low)/2.0;//!!!
             double r = (4.0*m*m + l*l)/(8.0*m);
             double s2 = 2.0 * r * asin(l / (2.0*r));
             if(s < s2)  high = m;
             else low = m;
         }
         printf("%.3lf\n", high);
     }
     return ;
 }