LeetCode Online Judge 1. Two Sum

刷个题，击败0.17%...

Given an array of integers, return indices of the two numbers such that they add up to a specific target.

You may assume that each input would have exactly one solution.

Example:

Given nums = [2, 7, 11, 15], target = 9,

Because nums[0] + nums[1] = 2 + 7 = 9,
return [0, 1].

code:

 public class Solution {
     public int[] TwoSum(int[] nums, int target) {
             int[] result=null;
             int i;
             for (i = ; i < nums.Length; i++)
             {
                 int j;
                 for (j = ; j < nums.Length; j++)
                 {
                     if(i != j)
                     {
                         if (nums[i] + nums[j] == target)
                         {
                             result = new int[] {j, i};
                         }
                     }
                 }
             }
            return result;
     }
 }

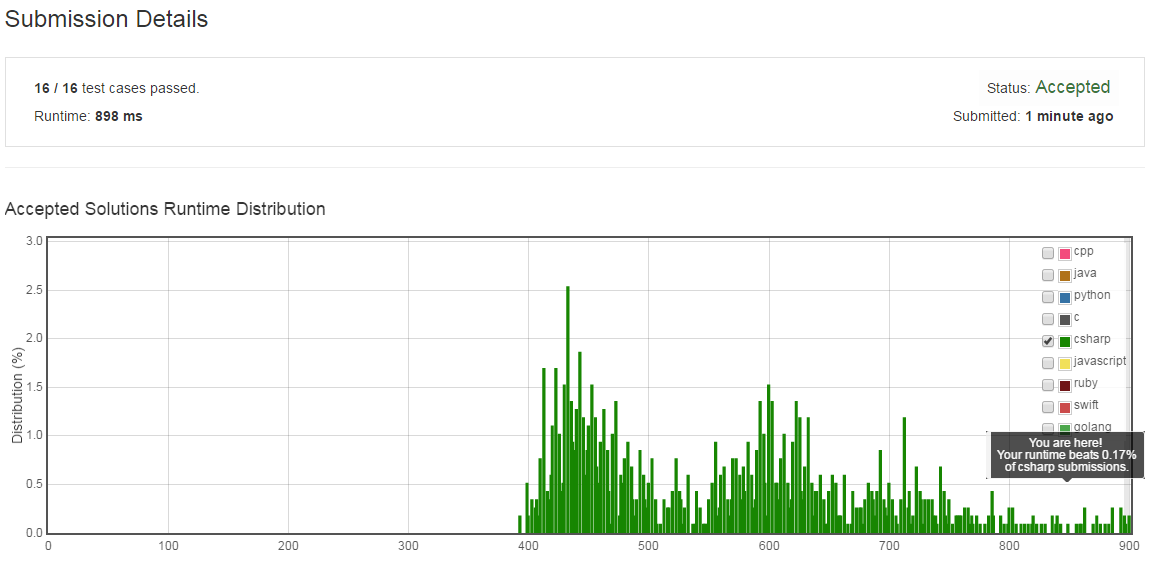
修改一下：

3.63%了...

     public int[] TwoSum(int[] nums, int target) {
             int[] result=null;
             int i;
             bool finishLoop = false;
             for (i = ; i < nums.Length; i++)
             {
                 int j;
                 for (j = ; j < nums.Length; j++)
                 {
                     if(i != j)
                     {
                         if (nums[i] + nums[j] == target)
                         {
                             result = new int[] {i, j};
                             finishLoop = true;
                             break;
                         }
                     }
                 }
                 if(finishLoop == true)
                     break;
             }
            return result;
     }

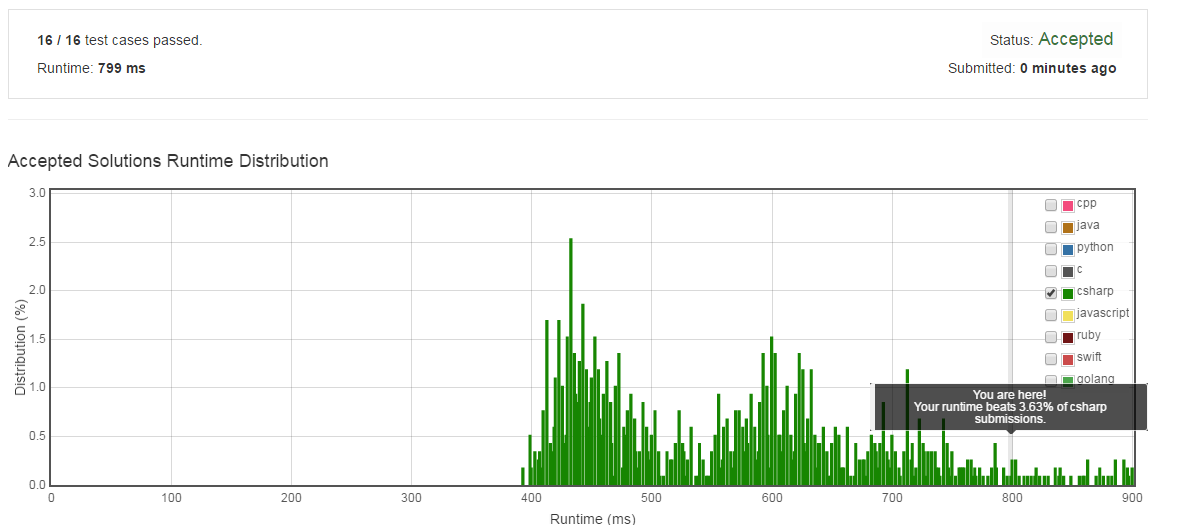
再改一下：

7.26%

             int[] result = null;
             int i;
             bool finishLoop = false;
             for (i = ; i < nums.Length; i++)
             {
                 int j;
                 for (j = ; j < nums.Length; j++)
                 {
                     if (i != j)
                     {
                         if (nums[i] + nums[j] == target)
                         {
                             result = new[] { i, j };
                             finishLoop = true;
                             break;
                         }
                     }
                 }
                 if (finishLoop)
                     break;
             }
             return result;

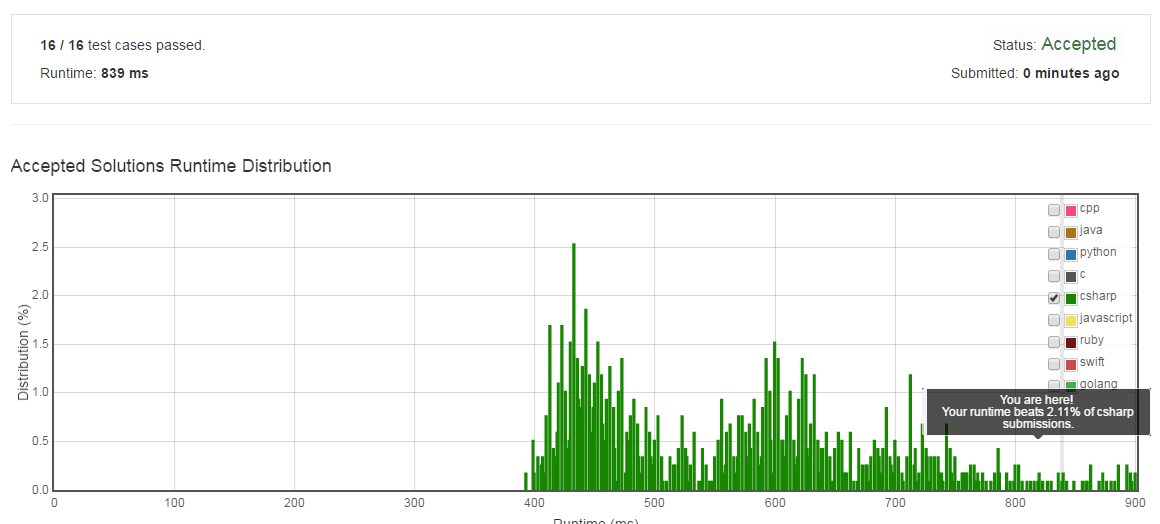
试试两个continue：

     public int[] TwoSum(int[] nums, int target) {
             int[] result = null;
             int i;
             bool finishLoop = false;
             for (i = ; i < nums.Length; i++)
             {
                 int j;
                 for (j = ; j < nums.Length; j++)
                 {
                     if (i == j) continue;
                     if (nums[i] + nums[j] != target) continue;
                         result = new[] { i, j };
                         finishLoop = true;

                 }
                 if (finishLoop)
                     break;
             }
             return result;
         }

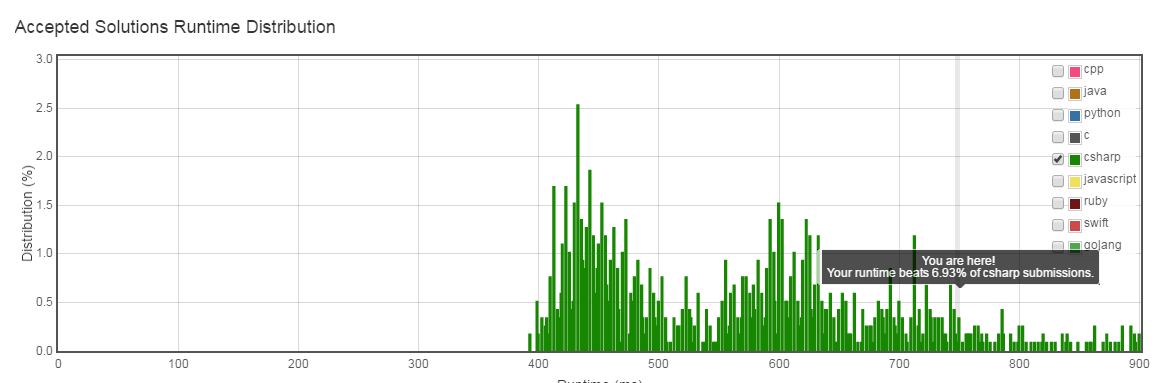
试试一个continue：

     public int[] TwoSum(int[] nums, int target) {
             int[] result = null;
             int i;
             bool finishLoop = false;
             for (i = ; i < nums.Length; i++)
             {
                 int j;
                 for (j = ; j < nums.Length; j++)
                 {
                     if (i == j) continue;
                     if (nums[i] + nums[j] == target)
                     {
                         result = new[] { i, j };
                         finishLoop = true;
                         break;
                     }

                 }
                 if (finishLoop)
                     break;
             }
             return result;
         }