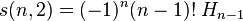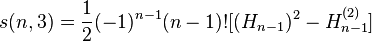斯特灵数 (Stirling数)
在组合数学,Stirling数可指两类数,都是由18世纪数学家James Stirling提出的。
第一类

第一类Stirling数是有正负的,其绝对值是 个元素的项目分作
个元素的项目分作 个环排列的方法数目。常用的表示方法有
个环排列的方法数目。常用的表示方法有 。
。
换个较生活化的说法,就是有 个人分成
个人分成 组,每组内再按特定顺序围圈的分组方法的数目。例如
组,每组内再按特定顺序围圈的分组方法的数目。例如 :
:
- {A,B},{C,D}
- {A,C},{B,D}
- {A,D},{B,C}
- {A},{B,C,D}
- {A},{B,D,C}
- {B},{A,C,D}
- {B},{A,D,C}
- {C},{A,B,D}
- {C},{A,D,B}
- {D},{A,B,C}
- {D},{A,C,B}
这可以用有向图来表示。
- 给定
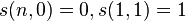 ,有递归关系
,有递归关系
递推关系的说明:考虑第n+1个物品,n+1可以单独构成一个非空循环排列,这样前n种物品构成k-1个非空循环排列,方法数为s(n,k-1);也可以前n种物品构成k个非空循环排列,而第n+1个物品插入第i个物品的左边,这有n*s(n,k)种方法。
 是调和数的推广。
是调和数的推广。
 是递降阶乘多项式的系数:
是递降阶乘多项式的系数:
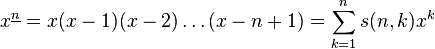
第二类
第二类Stirling数是 个元素的集定义k个等价类的方法数目。常用的表示方法有
个元素的集定义k个等价类的方法数目。常用的表示方法有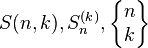 。
。
换个较生活化的说法,就是有 个人分成
个人分成 组的分组方法的数目。例如有甲、乙、丙、丁四人,若所有人分成1组,只有所有人在同一组这个方法,因此
组的分组方法的数目。例如有甲、乙、丙、丁四人,若所有人分成1组,只有所有人在同一组这个方法,因此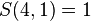 ;若所有人分成4组,只可以人人独立一组,因此
;若所有人分成4组,只可以人人独立一组,因此 ;若分成2组,可以是甲乙一组、丙丁一组,或甲丙一组、乙丁一组,或甲丁一组、乙丙一组,或其中三人同一组另一人独立一组,即是:
;若分成2组,可以是甲乙一组、丙丁一组,或甲丙一组、乙丁一组,或甲丁一组、乙丙一组,或其中三人同一组另一人独立一组,即是:
- {A,B},{C,D}
- {A,C},{B,D}
- {A,D},{B,C}
- {A},{B,C,D}
- {B},{A,C,D}
- {C},{A,B,D}
- {D},{A,B,C}
因此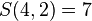 。
。
- 给定
 ,有递归关系
,有递归关系
- 递推关系的说明:考虑第n个物品,n可以单独构成一个非空集合,此时前n-1个物品构成k-1个非空的不可辨别的集合, 方法数为S(n-1,k-1);也可以前n-1种物品构成k个非空的不可辨别的 集合,第n个物品放入任意一个中,这样有k*S(n-1,k)种方法。




 是二项式系数,B_n是贝尔数。
是二项式系数,B_n是贝尔数。
两者关系
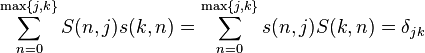
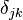 是克罗内克尔δ。
是克罗内克尔δ。
斯特灵数 (Stirling数)的更多相关文章
- 斯特灵(Stirling)数
http://zh.wikipedia.org/wiki/%E6%96%AF%E7%89%B9%E7%81%B5%E6%95%B0 第一类:n个元素分成k个非空循环排列(环)的方法总数 递推式:s(n ...
- Bell(hdu4767+矩阵+中国剩余定理+bell数+Stirling数+欧几里德)
Bell Time Limit:3000MS Memory Limit:32768KB 64bit IO Format:%I64d & %I64u Submit Status ...
- cf932E. Team Work(第二类斯特灵数 组合数)
题意 题目链接 Sol 这篇题解写的非常详细 首先要知道第二类斯特灵数的一个性质 \[m^n = \sum_{i = 0}^m C_{n}^i S(n, i) i!\] 证明可以考虑组合意义:\(m^ ...
- HDU4372-Count the Buildings【第一类Stirling数】+【组合数】
<题目链接> <转载于 >>> > 题目大意: N座高楼,高度均不同且为1~N中的数,从前向后看能看到F个,从后向前看能看到B个,问有多少种可能的排列数. 0 ...
- lightOJ 1326 Race(第二类Stirling数)
题目链接:http://lightoj.com/volume_showproblem.php?problem=1326 题意:有n匹马赛跑.问有多少种不同的排名结果.可以有多匹马的排名相同. 思路:排 ...
- hdu 4372 第一类stirling数的应用/。。。好题
/** 大意: 给定一系列楼房,都在一条水平线上,高度从1到n,从左侧看能看到f个, 从右侧看,能看到b个,问有多少种这样的序列.. 思路: 因为肯定能看到最高的,,那我们先假定最高的楼房位置确定,那 ...
- HDU 3625 Examining the Rooms:第一类stirling数
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=3625 题意: 有n个房间,每个房间里放着一把钥匙,对应能开1到n号房间的门. 除了1号门,你可以踹开任 ...
- HDU 4372 Count the Buildings:第一类Stirling数
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=4372 题意: 有n栋高楼横着排成一排,各自的高度为1到n的一个排列. 从左边看可以看到f栋楼,从右边看 ...
- 整理一点与排列组合有关的问题[组合数 Stirling数 Catalan数]
都是数学题 思维最重要,什么什么数都没用,DP直接乱搞(雾.. 参考LH课件,以及资料:http://daybreakcx.is-programmer.com/posts/17315.html 做到有 ...
随机推荐
- CSS效果
<%@ Page Language="C#" AutoEventWireup="true" CodeFile="Default.aspx.cs& ...
- LA 3295 (计数 容斥原理) Counting Triangles
如果用容斥原理递推的办法,这道题确实和LA 3720 Highway很像. 看到大神们写的博客,什么乱搞啊,随便统计一下,这真的让小白很为难,于是我决定用比较严格的语言来写这篇题解. 整体思路很简单: ...
- HDU 5284 wyh2000 and a string problem(字符串,水)
题意:比如给你一个串,要求判断wyh是不是它的子序列,那么你只需要找一个w,找一个y,再找一个h,使得w在y前面,y在h前面即可.有一天小学生拿着一个串问他“wyh是不是这个串的子序列?”.但是wyh ...
- 【又见LCS】NYOJ-37 回文字符串
[题目链接] 回文字符串 时间限制:3000 ms | 内存限制:65535 KB 难度:4 描述 所谓回文字符串,就是一个字符串,从左到右读和从右到左读是完全一样的,比如"aba& ...
- jsp防盗链代码
// 禁止缓存 response.setHeader("Cache-Control", "no-store"); response.setHeader( ...
- Oracle权限一览表
权限 所能实现的操作 分析 ANALYZE ANY 分析数据库中的任何表.簇或索引 审计 AUDIT ANY 审计数据库中的任何模式对象 AUDIT SYSTEM 启用与停用语句和特权的审计选项 ...
- 【转】traits技术及模板偏特化
#include <iostream> using namespace std; struct __xtrue_type { }; // define two mark-type stru ...
- [转] c#中 多线程访问winform控件
原文 c#中多线程访问winform控件的若干问题小结 我们在做winform应用的时候,大部分情况下都会碰到使用多线程控制界面上控件信息的问题.然而我们并不能用传统方法来解决这个问题,下面我将详细的 ...
- 手势解锁自定义View
package com.rxx.view; import java.util.ArrayList; import java.util.List; import java.util.Timer; imp ...
- 35、Android 性能优化、内存优化
http://blog.csdn.net/a_asinceo/article/details/8222104 http://blog.csdn.net/a_asinceo/article/detail ...