hdoj 2044一只小蜜蜂...【斐波那契变形】

一只小蜜蜂...

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 48153    Accepted Submission(s):
17558

Problem Description

有一只经过训练的蜜蜂只能爬向右侧相邻的蜂房，不能反向爬行。请编程计算蜜蜂从蜂房a爬到蜂房b的可能路线数。
其中，蜂房的结构如下所示。

 

Input

输入数据的第一行是一个整数N,表示测试实例的个数，然后是N
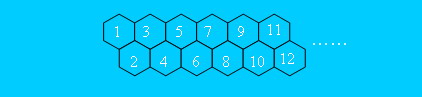
行数据，每行包含两个整数a和b(0<a<b<50)。

 

Output

对于每个测试实例，请输出蜜蜂从蜂房a爬到蜂房b的可能路线数，每个实例的输出占一行。

 

Sample Input

2

1 2

3 6

 

Sample Output

1

3

 

真的是被long long型折磨的很惨啊  好多次都错在这   此题符合菲波那切数列规律f[i]=f[i-1]+f[i-2]

#include<stdio.h>
#include<string.h>
long long f[100];
void fib()
{
	int j,i;
	f[1]=1;
	f[2]=2;
	for(i=3;i<55;i++)
	{
		f[i]=f[i-1]+f[i-2];
	}
}
int main()
{
	int n,m,j,i,t;
	scanf("%d",&t);
	fib();
	while(t--)
	{
		scanf("%d%d",&n,&m);
		printf("%lld\n",f[m-n]);
	}
	return 0;
}