为什么选择我--ReactJS

在页面中如何大面积操作DOM的话,性能肯定是一个很大的问题,然而聪明的ReactJS实现了Virtual DOM技术，这是他的亮点之一。将组件的DOM结构映射到这个Virtual DOM对象上，并且ReactJS还实现了一套Diff算法，这也是他亮点之一。当需要更新组件的时候，会通过Diff算法找到要变更的内容，最后，在把这个修改更新到实际的DOM节点上，所以，组件更新实际上不是真的渲染整个DOM树，而是指更新需要修改的DOM节点，这样在性能上会比原生DOM快很多。

那么这个Virtual DOM到底是什么？假设我们要创建一个组件，其结构如下:

 <ul>
     <li>
         A
     </li>
     <li>
         <ul>
             <li>
                 B
             </li>
         </ul>
     </li>
 </ul>

然后我们开始创建原生组件：

 //用JSX实现的
 var root = <ul>
         <li>A</li>
         <li>
             <ul>
                 <li>
                     B
                 </li>
             </ul>
         </li>
     </ul>;
 //用javascript实现的
 var A = React.createElement('li',null,'A');
 var B = React.createElement('ul',null,React.createElement('li',null,'B'));
 var root = React.createElement('ul',null,A,B);
 //输出虚拟的DOM结构
 console.log(root);

打开控制台我们就能看到输出的一个javascript的对象，没错这就是我们所说的Virtual DOM对象；

接下来我们看看Diff算法在ReactJS中的体现,首先我们借助浏览器中的MutationObderver功能,对页面元素进行监听

 'use strict';
 const mutation = window.MutationObserver
                 ||window.WebKitMutationObserver
                 ||window.MozMutationObserver;
 if(!!mutation){
     const mutationObserver = new mutation((item) => {
         item.forEach((item) => {
             console.log(item);
         });
     });
     const options = {
         "childList" : true,
         "attributes" : true,
         "characterData" : true,
         "subtree" : true,
         "attributeOldValue" : true,
         "characterDataOldValue" : true
     };
     mutationObserver.observe(document.body,options);
 }

然后再把ReactJS组件的生命周期进行封装，便于组件来调用

 'use strict';
 const LifeCycle = name => {
     let obj = {
         name : name
     };
     return Object.assign(obj,Cycle);
 };
 const Cycle = {
     getDefaultProps:function(){
         console.log(this.name,'getDefaultProps');
         return {};
     },
     getInitialState:function(){
         console.log(this.name,'getInitailState');
         return {};
     },
     componentWillMount:function(){
         console.log(this.name,'componentWillMount');
     },
     componentDidMount:function(){
         console.log(this.name,'componentDidMount');
     },
     componentWillRecieveProps:function(){
         console.log(this.name,'componentWillRecieveProps');
     },
     shouldComponentUpdate:function(){
         console.log(this.name,'shouldComponentUpdate');
         return true;
     },
     componentWillUpdate:function(){
         console.log(this.name,'componentWillUpdate');
     },
     componentDidUpdate:function(){
         console.log(this.name,'componentDidUpdate');
     },
     componentWillUnmount:function(){
         console.log(this.name,'componentWillUnmount');
     }
 }; 

接着定义需要用到的组件

 'use strict';
 //A组件
 let A = React.createClass({
     mixins:[LifeCycle('A')],
     render:function(){
         console.log('A','render');
         return (
             <ul>
                 <li>A</li>
                 <li>
                     <ul>
                         {this.props.children}
                     </ul>
                 </li>
             </ul>
         );
     }
 });
 //B组件
 let B = React.createClass({
     mixins:[LifeCycle('B')],
     render:function(){
         console.log('B','render');
         return (
             <li>B</li>
         );
     }
 });
 //C组件
 let C = React.createClass({
     mixins:[LifeCycle('C')],
     render:function(){
         console.log('C','render');
         return (
             <li>C</li>
         );
     }
 });
 //D组件
 let D = React.createClass({
     mixins:[LifeCycle('D')],
     render:function(){
         console.log('D','render');
         return (
             <li>D</li>
         );
     }
 });

最后，定义我们的主逻辑

 console.log('----------------first-----------------');
 React.render(
     <A><B></B><C></C></A>,
     document.body
 );

 setTimeout(() => {
     console.log('-----------------second--------------');
     React.render(
         <A><B></B><D></D><C></C></A>,
         document.body
     );
 },1000);

常规的做法就是将B和C组件先删除，然后依次创建和插入A,B,C组件。接下来我们打开浏览器的控制台看下ReactJS是怎么做的

          

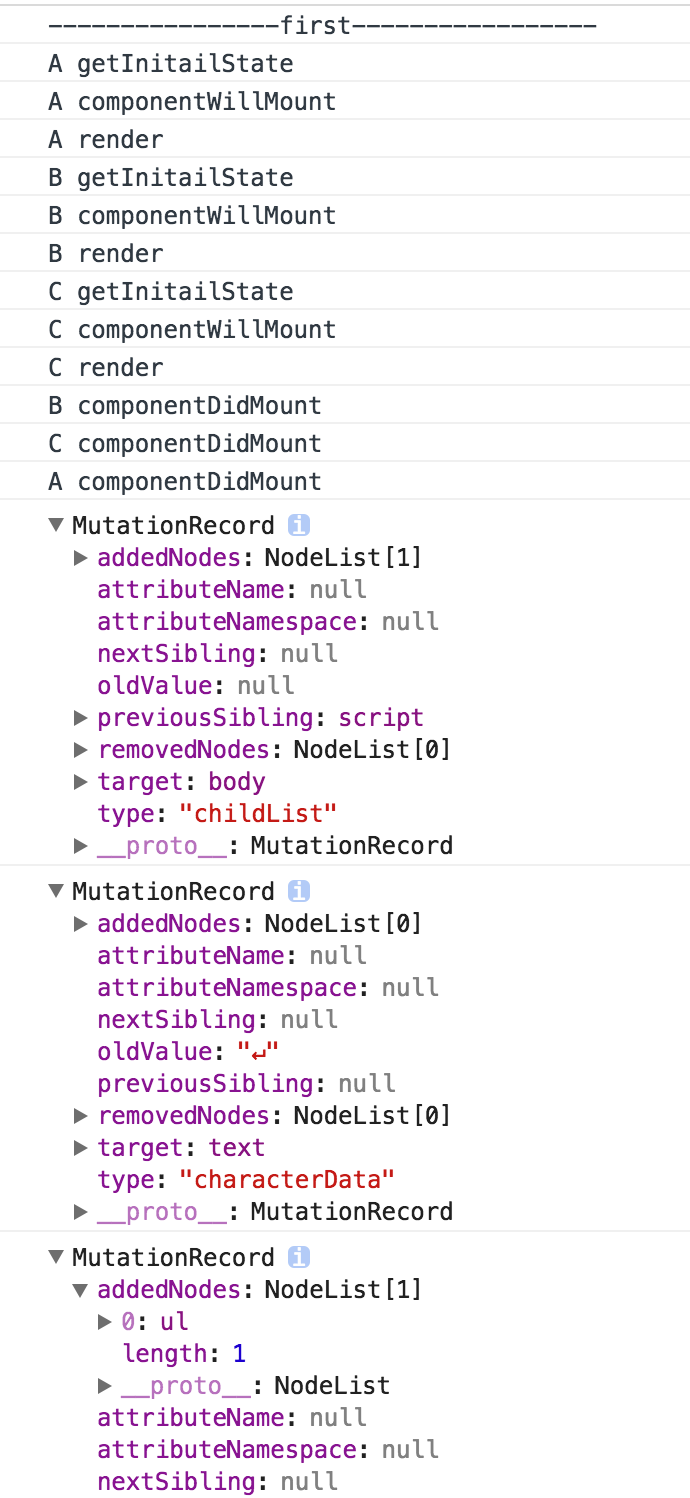
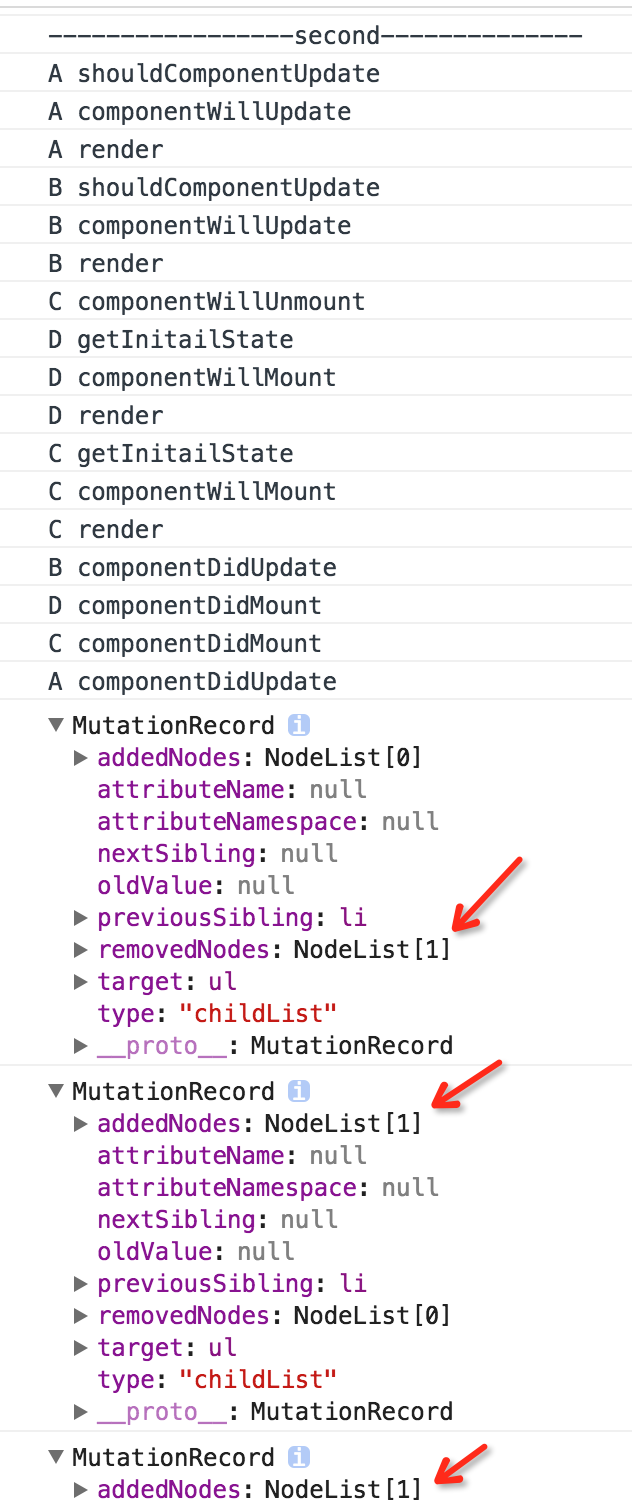
从日志中可以看出，React的Diff算法的结果是，A组件不变，先将C组件进行删除，然后在创建D组件并插入D组件，最后创建并插入C组件，这比我们常规的做法省去了对B组件的删除操作。这样其实并没有将Diff算法的作用发挥到极限。下面我们调整下逻辑代码：

 console.log('----------------first-----------------');
 React.render(
     <A key="A"><B key="B"></B><C key="C"></C></A>,
     document.body
 );

 setTimeout(() => {
     console.log('-----------------second--------------');
     React.render(
         <A key="A"><B key="B"></B><D key="D"></D><C key="C"></C></A>,
         document.body
     );
 },1000);

主要的修改就是给每个组件加了一个key属性，此时再来运行下代码看下控制台的日志：

       

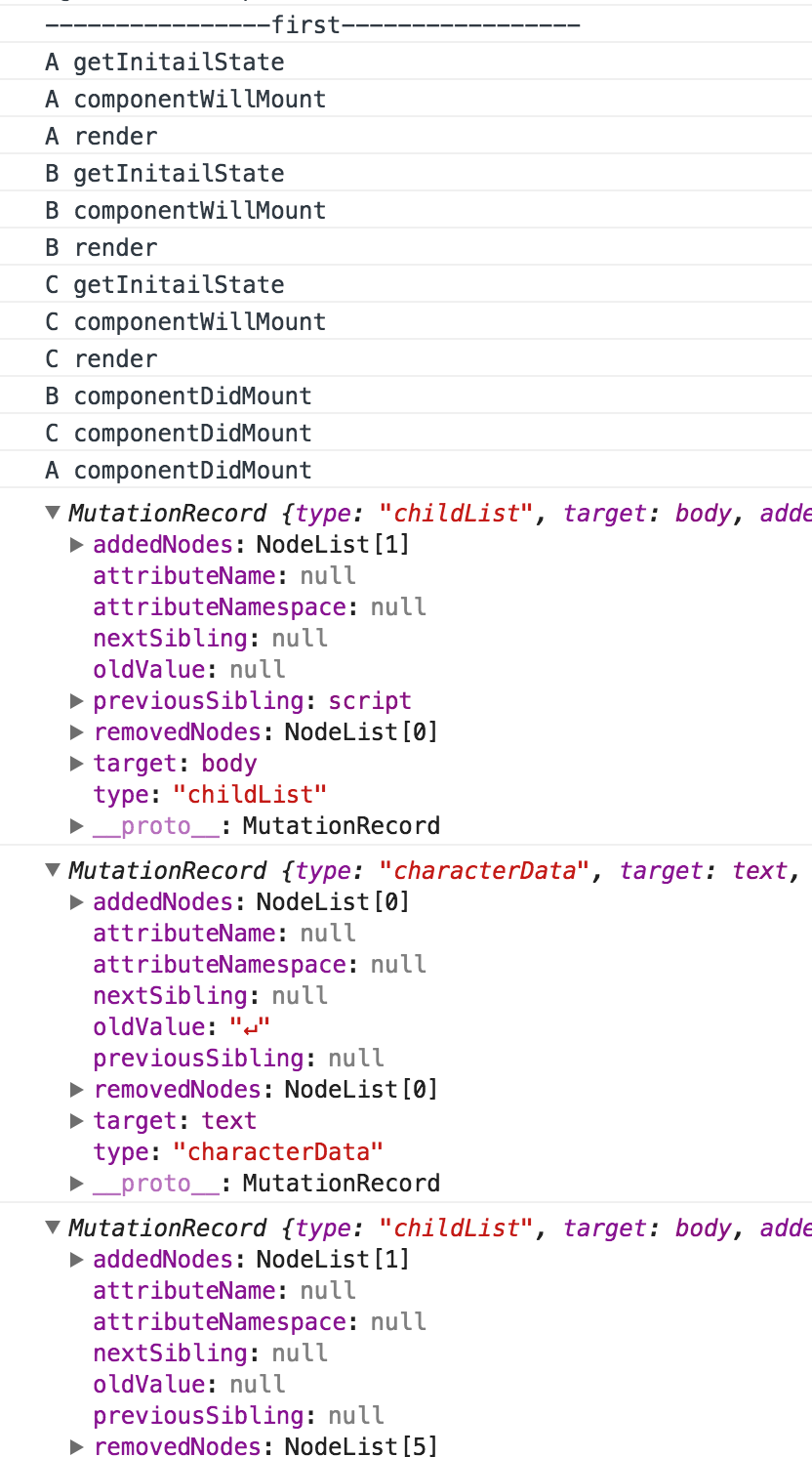
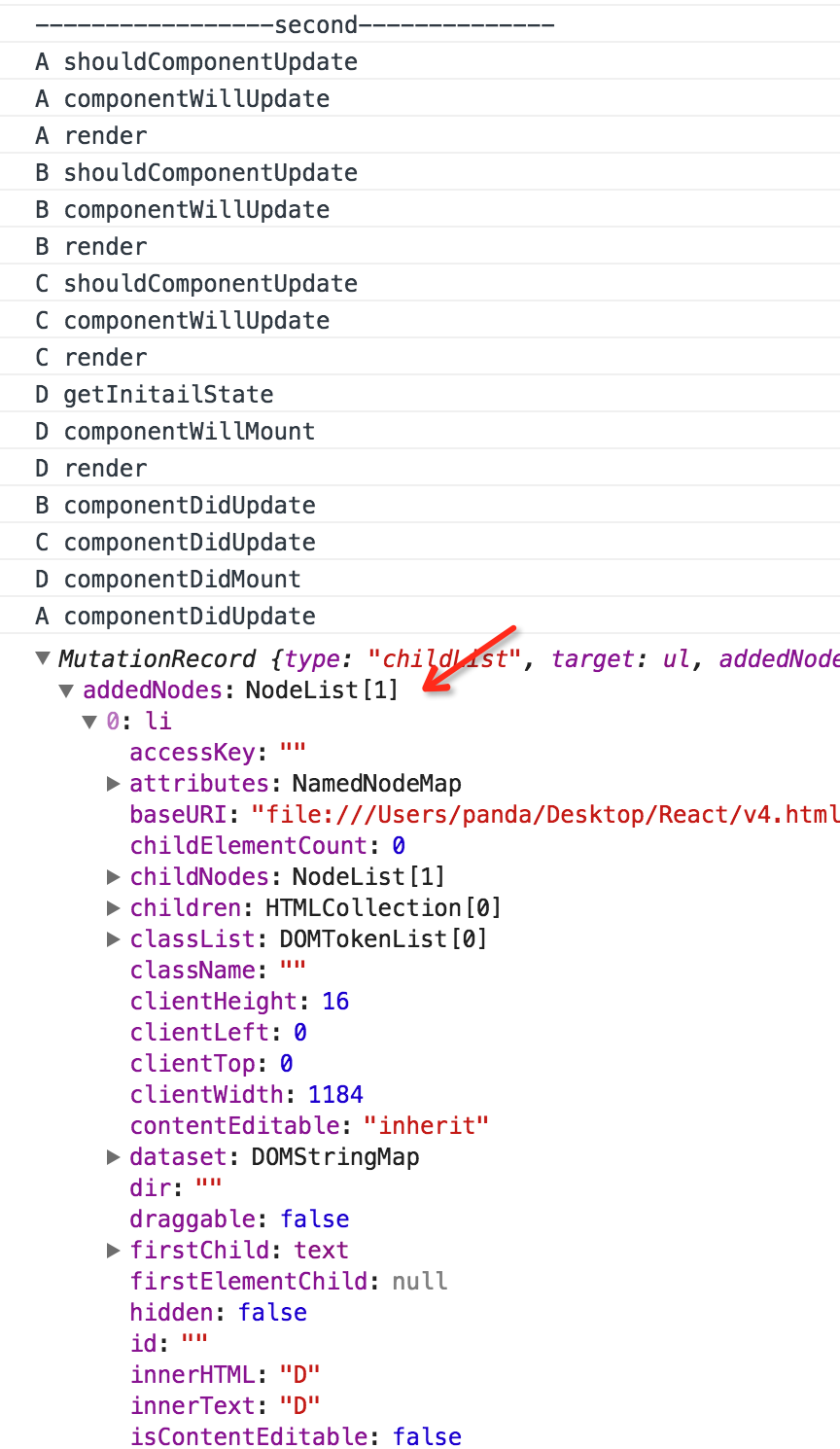
可以看出，这次Diff算法与之前的有很大的不同。B组件不变，C组件不变，只是在C组件之前创建并插入了D组件。

以上便是Virtual DOM和Diff算法的一些简单的使用和分析，学习来源：

http://calendar.perfplanet.com/2013/diff/ 《React Native入门与实践》