UVA10054-The Necklace(无向图欧拉回路——套圈算法)
Time Limit: 3000 mSec
![]() Problem Description
Problem Description
Input
The input contains T test cases. The first line of the input contains the integer T. The first line of each test case contains an integer N (5 ≤ N ≤ 1000) giving the number of beads my sister was able to collect. Each of the next N lines contains two integers describing the colors of a bead. Colors are represented by integers ranging from 1 to 50.
![]() Output
Output
![]() Sample Input
Sample Input
![]() Sample Output
Sample Output
some beads may be lost
1 3
3 4
4 2
2 2
#include <bits/stdc++.h> using namespace std; #define REP(i, n) for (int i = 1; i <= (n); i++)
#define sqr(x) ((x) * (x)) const int maxn = + ;
const int maxm = + ;
const int maxs = + ; typedef long long LL;
typedef pair<int, int> pii;
typedef pair<double, double> pdd; const LL unit = 1LL;
const int INF = 0x3f3f3f3f;
const LL mod = ;
const double eps = 1e-;
const double inf = 1e15;
const double pi = acos(-1.0); int n, iCase;
int deg[maxn], gra[maxn][maxn]; void dfs(int u)
{
for (int i = ; i <= ; i++)
{
if (gra[u][i])
{
gra[u][i]--;
gra[i][u]--;
dfs(i);
cout << i << " " << u << endl;
}
}
} int main()
{
ios::sync_with_stdio(false);
cin.tie();
freopen("input.txt", "r", stdin);
//freopen("output.txt", "w", stdout);
int T;
cin >> T;
while (T--)
{
cin >> n;
cout << "Case #" << ++iCase << endl;
memset(deg, , sizeof(deg));
memset(gra, , sizeof(gra));
int u, v;
for (int i = ; i < n; i++)
{
cin >> u >> v;
gra[u][v]++, gra[v][u]++;
deg[u]++, deg[v]++;
}
bool ok = true;
for (int i = ; i <= ; i++)
{
if (deg[i] % )
{
ok = false;
break;
}
}
if (!ok)
{
cout << "some beads may be lost" << endl;
}
else
{
dfs(v);
}
if (T)
cout << endl;
}
return ;
}
UVA10054-The Necklace(无向图欧拉回路——套圈算法)的更多相关文章
- UVa 10054 The Necklace(无向图欧拉回路)
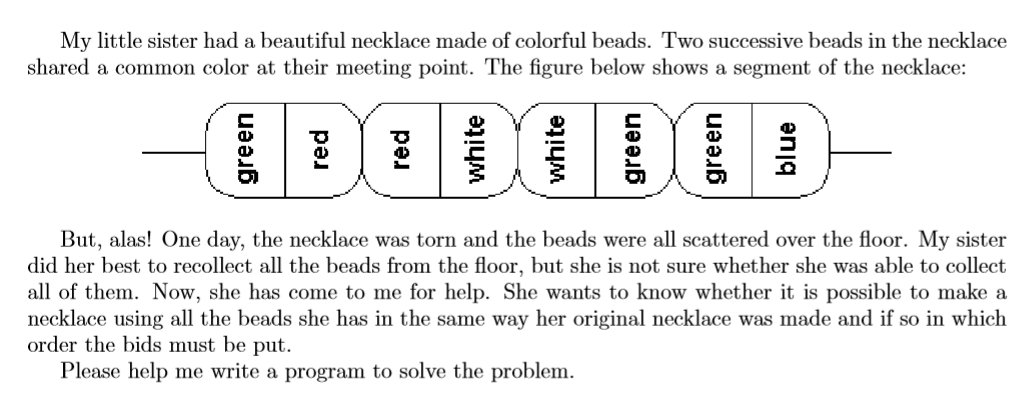
My little sister had a beautiful necklace made of colorful beads. Two successive beads in the neckla ...
- UVA-10054 The Necklace (欧拉回路)
题目大意:有n个珠子,珠子两边的颜色已知,问能否连成一条项链.(两个珠子可以项链当且仅当一个珠子的一边颜色与另一个珠子的另一边颜色相同). 题目分析:欧拉回路.将颜色视作节点,珠子当做边,问题变成了找 ...
- UOJ 117 欧拉回路(套圈法+欧拉回路路径输出+骚操作)
题目链接:http://uoj.ac/problem/117 题目大意: 解题思路:先判断度数: 若G为有向图,欧拉回路的点的出度等于入度. 若G为无向图,欧拉回路的点的度数位偶数. 然后判断连通性, ...
- UVA10054 The Necklace
UVA10054 The Necklace 链接:http://acm.hust.edu.cn/vjudge/problem/viewProblem.action?id=18806 [思路] 欧拉回路 ...
- SGU 455 Sequence analysis(Cycle detection,floyd判圈算法)
题目链接:http://acm.sgu.ru/problem.php?contest=0&problem=455 Due to the slow 'mod' and 'div' operati ...
- UVA 11549 CALCULATOR CONUNDRUM(Floyd判圈算法)
CALCULATOR CONUNDRUM Alice got a hold of an old calculator that can display n digits. She was bore ...
- UVA 11549 Calculator Conundrum (Floyd判圈算法)
题意:有个老式计算器,每次只能记住一个数字的前n位.现在输入一个整数k,然后反复平方,一直做下去,能得到的最大数是多少.例如,n=1,k=6,那么一次显示:6,3,9,1... 思路:这个题一定会出现 ...
- leetcode202(Floyd判圈算法(龟兔赛跑算法))
Write an algorithm to determine if a number is "happy". 写出一个算法确定一个数是不是快乐数. A happy number ...
- Floyd判圈算法
Floyd判圈算法 leetcode 上 编号为202 的happy number 问题,有点意思.happy number 的定义为: A happy number is a number defi ...
随机推荐
- Linux学习笔记(一):常用命令(1)
经过统计Linux中能够识别的命令超过3000种,当然常用的命令就远远没有这么多了,按照我的习惯,我把已经学过的Linux常用命令做了以下几个方面的分割: 1.文件处理命令 2.文件搜索命令 3.帮助 ...
- EF三种编程方式图文详解
Entity Framework4.1之前EF支持“Database First”和“Model First”编程方式,从EF4.1开始EF开始支持支持“Code First”编程方式,今天简单看一下 ...
- window环境下使用filezilla server搭建ftp服务器
前言 在做项目的时候,需要提供ftp服务,开始的时候使用微软自动的iss上的ftp服务,一段时间后发现无法自定义用户,只能使用系统的用户,使用起来很不方便,在权限管理方面也是不太好.所以换用了file ...
- PE知识复习之PE的绑定导入表
PE知识复习之PE的绑定导入表 一丶简介 根据前几讲,我们已经熟悉了导入表结构.但是如果大家尝试过打印导入表的结构. INT IAT的时候. 会出现问题. PE在加载前 INT IAT表都指向一个名称 ...
- [零]java8 函数式编程入门官方文档中文版 java.util.stream 中文版 流处理的相关概念
前言 本文为java.util.stream 包文档的译文 极其个别部分可能为了更好理解,陈述略有改动,与原文几乎一致 原文可参考在线API文档 https://docs.oracle.com/jav ...
- jstat命令查看jvm的GC情况 (以Linux为例)
jstat命令可以查看堆内存各部分的使用量,以及加载类的数量.命令的格式如下: jstat [-命令选项] [vmid] [间隔时间/毫秒] [查询次数] 注意!!!:使用的jdk版本是jdk8. ...
- Java开发笔记(八)五种算术运算符
计算机科学起源于数学,早期的计算机也确实多用于数学运算,以至于后来的各路编程语言,仍然保留着古老的加减乘除四则运算.这四则运算在Java语言中有专门的运算符加以表示,像加法符号“+”对应Java的“+ ...
- 解决ajaxfileupload上传文件在IE浏览器返回data为空问题
关于ajaxfileupload,建议还是别用,已经没有人维护的脚本了,笔者就是入了这个坑. 在IE浏览器中ajaxfileupload返回data为空 jq.ajaxFileUpload ( { u ...
- 委托(4).net 3.5中的委托
.net 3.5引入了Linq,lambda表达式,所以委托的创建变得更加简单和优雅了. .net 3.5中的委托 引入lambda表达式后,就不需要再使用匿名方法了,使得创建委托的方式更加简单和优雅 ...
- 如何清理Docker占用的磁盘空间?
摘要:用了 Docker,好处挺多的,但是有一个不大不小的问题,它会一不小心占用太多磁盘,这就意味着我们必须及时清理. 作为一个有信仰的技术公司,我们Fundebug的后台采用了酷炫的全 Docker ...
