LCA-RMQ+欧拉序

还是那一道洛谷的板子题来说吧

传送门

其实好几天之前就写了

结果dr实在是太弱了

没有那么多的精力

于是就一直咕咕咕了

哎

今天终于补上来了

LCA概念传送门

RMQ传送门

这个算法是基于RMQ和欧拉序的算法

什么是Rmq？

 

RMQ (Range Minimum/Maximum Query)问题是指：

对于长度为n的数列A，

回答若干询问RMQ(A,i,j)(i,j<=n)，

返回数列A中下标在i,j里的最小(大）值，

也就是说，RMQ问题是指求区间最值的问题。

解决Rmq问题常用ST算法。

 

ST算法时间复杂度：
 预处理O(nlogn)
 单次查询O(1)

 

欧拉序？
 欧拉序是一种树的遍历顺序，其他还有dfs序，这些序具有一定的性质。

 欧拉序是树dfs过程中经过 结点的顺序。

若已1->2->4->5->6->7->3的顺序dfs树

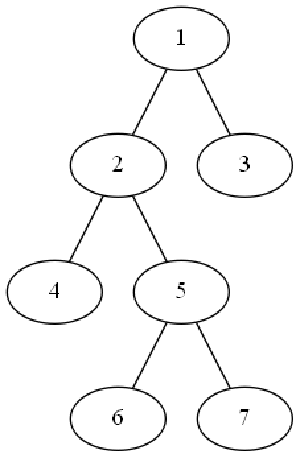
即每经过一次结点就记录一次，

n个结点的树有2n-1个记录

基于Rmq和欧拉序的Lca算法：

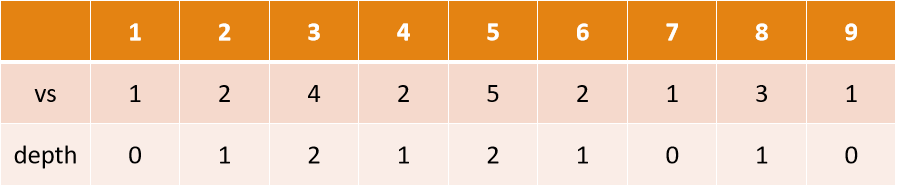
预处理出树的欧拉序，预处理id,vs,depth数组

id[u]表示结点u第一次被访问时的下标，

vs[i]表示欧拉序中第i个结点的编号,

depth[i]表示欧拉序中第i个结点的深度。

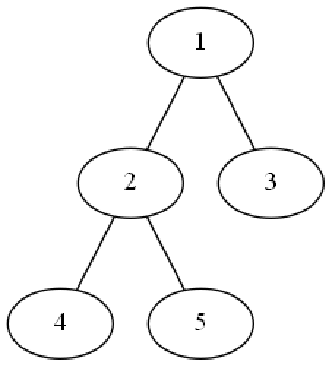
假设dfs顺序1->2->4->5->3

要求Lca(u,v)，例如Lca(4,5)，

根据dfs的性质，在第一次访问完结点4及其子树，回溯，

再第一次访问到5的过程中，途中访问过的深度最小的结点必是Lca(4,5)

 

Rmq问题。Lca(u,v)=vs[id[u]<=i<=id[v]中depth[i]最小的i]

（假设id[u]<id[v]）

 

 

#include<cstdio>
#include<algorithm>
using namespace std;

const int maxn = ;
const int maxm = ;
int head[maxn],nxt[maxm],to[maxm],cnt;
int id[maxm],vis[maxm],depth[maxm],tot;
int f[maxm][],lg[maxm];

inline int read()
{
    int sum = ,p = ;
    char ch = getchar();
    while(ch < '' || ch > '')
    {
        if(ch == '-')
            p = -;
        ch = getchar();
    }
    while(ch >= '' && ch <= '')
    {
        (sum *= )+= ch - '';
        ch = getchar();
    }
    return sum * p;
}

void add(int x,int y)//链式前向星--加边
{
    nxt[++cnt] = head[x];
    to[cnt] = y;
    head[x] = cnt;
    return;
}

void dfs(int u,int fa,int dep)
{
    id[u] = ++tot;
    vis[tot] = u;
    depth[tot] = dep;
    for(int i = head[u];i;i = nxt[i])
    {
        int v = to[i];
        if(v == fa)
            continue;
        dfs(v,u,dep+);
        vis[++tot] = u;
        depth[tot] = dep;
    }
    return;
}

void RMQ()
{
    for(int i = ;i <= tot;i++)
        lg[i] = lg[i - ] + ( << lg[i - ] == i);
    for(int i = ;i <= tot;i++)
        f[i][] = i;
    for(int j = ;( << j) <= tot;j++)
        for(int i = ;i + ( << j) -  <= tot;i++)
        {
            int a = f[i][j-];
            int b = f[i + ( << (j - ))][j - ];
            if(depth[a] <= depth[b])
                f[i][j] = a;
            else
                f[i][j] = b;
        }
    return;
}

int    st(int x,int y)
{
    int r = id[x];
    int l = id[y];
    if(r < l)
        swap(r,l);
    int k = lg[r - l + ] - ;
    int a = f[l][k];
    int b = f[r - ( << k) + ][k];
    if(depth[a] <= depth[b])
        return vis[a];
    else
        return vis[b];
}

int main()
{
    int n = read(),m = read(),s = read();
    int x,y;
    for(int i = ;i < n;i++)
    {
        x = read(),y = read();
        add(x,y);
        add(y,x);
    }
    dfs(s,,);
    RMQ();
    for(int i = ;i <= m;i++)
    {
        x = read(),y = read();
        printf("%d\n",st(x,y));
    }
    return ;
}