机器学习实战（笔记）------------KNN算法

1.KNN算法

KNN算法即K-临近算法，采用测量不同特征值之间的距离的方法进行分类。

以二维情况举例：

        假设一条样本含有两个特征。将这两种特征进行数值化，我们就可以假设这两种特种分别为二维坐标系中的横轴和纵轴，将一个样本以点的形式表示在坐标系中。这样，两个样本直接变产生了空间距离，假设两点之间越接近越可能属于同一类的样本。如果我们有一个待分类数据，我们计算该点与样本库中的所有点的距离，取前K个距离最近的点，以这K个中出现次数最多的分类作为待分类样本的分类。这样就是KNN算法。

优点：精度高，对异常值不敏感，无数据输入假定

缺点：时间、空间复杂度太大（比如每一次分类都需要计算所有样本点与测试点的距离）

2.KNN算法的Python实现

import operator
from os import listdir

import matplotlib
import matplotlib.pyplot as plt
from numpy import array, shape, tile, zeros

#分类方法
#inx 待分类向量
#dataSet 测试数据
#labels 测试数据标签
#k 取前k个作为样本
def classify(inX,dataSet,labels,k):
    dataSetSize=dataSet.shape[0]
    diffMat=tile(inX,(dataSetSize,1))-dataSet #tile方法利用输入数组进行扩充
    sqDiffMat=diffMat**2
    sqDistance=sqDiffMat.sum(axis=1)
    distance=sqDistance**0.5
    index=distance.argsort() #返回按从小到大的顺序排序后的元素下标
    classCount={}
    for i in range(k):
        lable=labels[index[i]]
        classCount[lable]=classCount.get(lable,0)+1
    #在python3中dict.iteritems()被废弃
    sortedClasssCount=sorted(classCount.items(),
    key=operator.itemgetter(1),reverse=True)
    return sortedClasssCount[0][0]

    代码传入的三个参数分别为待分类向量，测试数据，测试数据标签。代码使用欧式距离公式计算向量点之间的距离。

\[d=\sqrt{(xA_0-xB_0)^2-（xA_1-xB_1)^2}
\]

• numpy.tile(A,reps)

  A指待输入数组，reps则决定A的重复次数

• sorted(iterable,cmp,key,reverse)

  这里利用了key参数使得使用字典中的value值进行排序

实例1：KNN算法改进约会网站配对效果

背景

假设A在利用约会网站进行约会，她将自己交往过的人分为三类：

• 不喜欢的人
• 魅力一般的人
• 极具魅力的人

A收集这些人的生活记录，从中提取中三类特征，存储在文本datingTestSet2中：

• 每年获得的飞行常客里程数
• 玩游戏视频所耗时间百分比
• 每周消耗的冰淇淋公升数

利用这三类特征和标签组成的样本库，我们可以在获得一个人的这三种特征的特征值的情况下，利用KNN算法判断该人是否会是A喜欢人

读取数据

我们将数据从文本中读出，并且以矩阵的形式进行存储

def file2matrix(filename):
    fr=open(filename)
    datalines=fr.readlines()
    numberoflines=len(datalines)
    returnMat=zeros((numberoflines,3))
    classlabelVector=[]
    index=0
    for line in datalines:
        line=line.strip()
        listfromline=line.split('\t')
        returnMat[index,:]=listfromline[0:3]
        classlabelVector.append(int(listfromline[-1]))
        index=index+1
    return returnMat,classlabelVector

分析数据

我们可以利用Matplotlib制作原始数据的散点图，观察特征

def analydata():
    a,b=file2matrix('datingTestSet2.txt')
    #创建一个图形实例
    fig=plt.figure()
    ax=fig.add_subplot(111)
    #scatter方法创建散点图
    #分析图像可以发现使用第一列和第二列数据特征更加明显
    ax.scatter(a[:,0],a[:,1],15.0*array(b),15.0*array(b))
    plt.show()

画图结果：

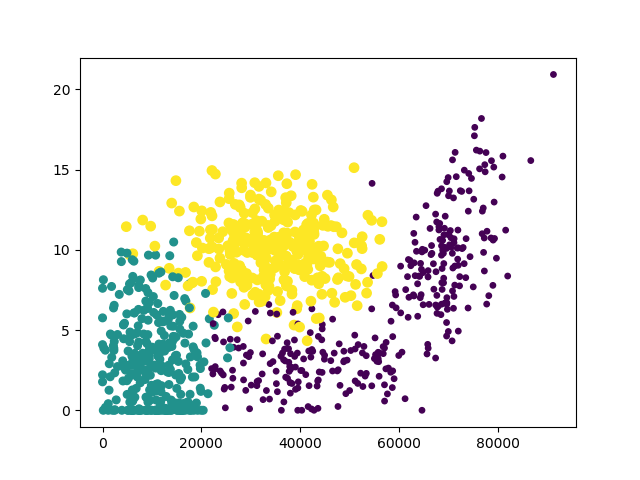
这里以“冰淇淋公斤数”和“玩视频游戏所耗时间百分比”作为横纵坐标特征最为明显

归一化数据

在数据分析和机器学习中，经常要进行数据归一化。因为不同的特征值使用不同的量度，上下限不同，使得有的特征产生的差值很大，而有的很小，会影响算法准确性。所以要先对数据预处理，进行数据归一化处理。

\[newValue=(oldValue-min)/(max-min)
\]

分类器与测试

我们利用KNN算法，以前10%的数据作为待分类数据，后90%的数据作为样本库测试数据，进行分类与测试

def datingClassTest():
    hoRatio=0.10
    datingDataMat,datingLables=file2matrix('datingTestSet2.txt')
    normMat=data2normal(datingDataMat)
    m=normMat.shape[0]
    numTestVecs=int(hoRatio*m)
    errorCount=0
    for i in range(numTestVecs):
        result=classify(normMat[i,:],normMat[numTestVecs:m,:],
        datingLables[numTestVecs:m],3)
        print("the classify come back with: %d,the real answer is: %d"
        %(result,datingLables[i]))
        if(result!=datingLables[i]):
            errorCount+=1.0
    print("error rate is:%f"%(errorCount/float(numTestVecs)))

测试结果，错误率大概在5%左右。

我们可以改变hoRatio和k的值，检查错误率是否发生变化

实例2：手写识别系统

背景

假设我们有一些手写数字，以如下形式保存：

00000000000001100000000000000000
00000000000011111100000000000000
00000000000111111111000000000000
00000000011111111111000000000000
00000001111111111111100000000000
00000000111111100011110000000000
00000001111110000001110000000000
00000001111110000001110000000000
00000011111100000001110000000000
00000011111100000001111000000000
00000011111100000000011100000000
00000011111100000000011100000000
00000011111000000000001110000000
00000011111000000000001110000000
00000001111100000000000111000000
00000001111100000000000111000000
00000001111100000000000111000000
00000011111000000000000111000000
00000011111000000000000111000000
00000000111100000000000011100000
00000000111100000000000111100000
00000000111100000000000111100000
00000000111100000000001111100000
00000000011110000000000111110000
00000000011111000000001111100000
00000000011111000000011111100000
00000000011111000000111111000000
00000000011111100011111111000000
00000000000111111111111110000000
00000000000111111111111100000000
00000000000011111111110000000000
00000000000000111110000000000000

这是一个32*32的矩阵，利用0代表背景，1来代表手写数字

对于这些数据，我们也可以利用KNN算法来识别写的是0~9中的哪里数字

注：存储数据的文件，例如：0_0.txt代码数字0的第一个手写样本数据

数据预处理：转换成测试向量

  数据使用32X32的矩阵形式存储，为了能够使用我们实现的KNN分类器，我们必须将其转化成1X1024的向量形式进行表示，也可以叫做降维，将二维数据转换成了一维数据

def img2vector(filename):
    fr=open(filename)
    returnVect=zeros((1,1024))
    for i in range(32):
        linestr=fr.readline()
        for j in range(32):
            returnVect[0,i*32+j]=int(linestr[j])
    return returnVect

使用KNN算法进行分类

  转换成向量以后，我们就可以使用我们实现的KNN分类器进行分类了

import operator
from os import listdir

import matplotlib
import matplotlib.pyplot as plt
from numpy import array, shape, tile, zeros

def handwritingClassTest():
    hwlabels=[]
    traingfilelist=listdir('digits/trainingDigits')
    m=len(traingfilelist)
    trainingDataMat=zeros((m,1024))
    for i in range(m):
        filenameStr=traingfilelist[i]
        fileStr=filenameStr.split('.')[0]
        label=int(fileStr.split('_')[0])
        hwlabels.append(label)
        trainingDataMat[i,:]=img2vector
        ('digits/trainingDigits/%s' % filenameStr)
    errorCount=0.0
    testfilelist=listdir('digits/testDigits')
    mTest=len(testfilelist)
    for i in range(mTest):
        filenameStr=testfilelist[i]
        fileStr=filenameStr.split('.')[0]
        label=int(fileStr.split('_')[0])
        testVector=img2vector('digits/testDigits/%s' %filenameStr)
        result=classify(testVector,trainingDataMat,hwlabels,3)
        print('come back with: %d,the real answer is: %d' % (int(result),label))
        if(int(result)!=label):
            errorCount=errorCount+1.0
    print('total number errors is :%f' % errorCount)
    print('error rate is :%f'% (errorCount/float(mTest)))

• os.listdir()

  利用该方法，可以得到指定目录里面的所有文件名