LightOJ 1203 Guarding Bananas (凸包最小顶角)

题目链接：LightOJ 1203

Problem Description

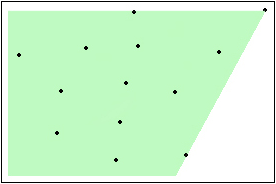
Once there was a lazy monkey in a forest. But he loved banana too much. One day there was a storm in the jungle and all the bananas fell from the trees. The monkey didn't want to lose any of the bananas. So, he wanted to find a banana such that he can eat that and he can also look after the other bananas. As he was lazy, he didn't want to move his eyes too wide. So, you have to help him finding the banana from where he can look after all the bananas but the degree of rotating his eyes is as small as possible. You can assume that the position of the bananas can be modeled as 2D points.

Here a banana is shown, from where the monkey can look after all the bananas with minimum eye rotation.

Input

Input starts with an integer \(T (\le 13)\), denoting the number of test cases.

Each case starts with a line containing an integer \(n (1 \le n \le 105)\) denoting the number of bananas. Each of the next \(n\) lines contains two integers \(x y (-10^9 \le x, y \le 10^9)\) denoting the co-ordinate of a banana. There can me more than one bananas in the same co-ordinate.

Output

For each case, print the case number and the minimum angle in degrees. Errors less than \(10^-6\) will be ignored.

Sample Input

2
1
4 4
4
0 0
10 0
10 10
2 1

Sample Output

Case 1: 0
Case 2: 45.0000000

Note

Dataset is huge. Use faster I/O methods.

Solution

题意：

给定若干个点的坐标，求凸包最小顶角。

思路

凸包

先求凸包，然后枚举所有顶角求最小值。

顶角求法：用两个向量的夹角求

\(\angle BAC\) 为向量 \(\overrightarrow {AB}\) 与 \(\overrightarrow {AC}\) 的夹角：

\[cos<\overrightarrow {AB}, \overrightarrow {AC}> = \frac{\overrightarrow {AB} ⋅ \overrightarrow {AC}}{|\overrightarrow {AB}| |\overrightarrow {AC}|}
\]

Code

#include <bits/stdc++.h>
using namespace std;
const double eps = 1e-8;
const double pi = acos(-1.0);
const int maxn = 1e5 + 10;

int n;
struct Point {
    double x, y;
    Point() {}
    Point(double a, double b) : x(a), y(b) {}
    bool operator<(const Point &b) const {
        if (x < b.x) return 1;
        if (x > b.x) return 0;
        return y < b.y;
    }
    Point operator-(const Point &b) {
        return Point(x - b.x, y - b.y);
    }
} p[maxn], stk[maxn];
typedef Point Vec;

int sgn(double x)  {
    if (fabs(x) <= eps)
        return 0;
    return x > 0 ? 1 : -1;
}

double dist(Point a, Point b) {
    return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}

double cross(Vec a, Vec b) {
    return a.x * b.y - a.y * b.x;
}

int Andrew() {
    sort(p + 1, p + 1 + n);
    int len = 0;
    for (int i = 1; i <= n; ++i) {
        while (len > 1 && sgn(cross(stk[len] - stk[len - 1], p[i] - stk[len - 1])) == -1) {
            len--;
        }
        stk[++len] = p[i];
    }
    int k = len;
    for (int i = n - 1; i >= 1; --i) {
        while (len > k && sgn(cross(stk[len] - stk[len - 1], p[i] - stk[len - 1])) == -1) {
            len--;
        }
        stk[++len] = p[i];
    }
    return len;
}

double angle(Point p, Point q, Point s) {
    double x1 = q.x - p.x, y1 = q.y - p.y;
    double x2 = s.x - p.x, y2 = s.y - p.y;
    double ans = (x1 * x2 + y1 * y2) / (sqrt(x1 * x1 + y1 * y1) * sqrt(x2 * x2 + y2 * y2));
    return acos(ans);
}
int main() {
    int T;
    scanf("%d", &T);
    int kase = 0;
    while(T--) {
        map<pair<double, double>, int> mp;
        n = 0;
        int cnt;
        scanf("%d", &cnt);
        for (int i = 1; i <= cnt; ++i) {
            double x, y;
            scanf("%lf%lf", &x, &y);
            if(mp[make_pair(x, y)] == 0) {
                mp[make_pair(x, y)] = 1;
                p[++n].x = x;
                p[n].y = y;
            }
        }

        if(n < 3) {
            printf("Case %d: 0\n", ++kase);
            continue;
        }
        int t = Andrew();
        double min_angle = angle(stk[1], stk[t - 1], stk[2]);
        for (int i = 2; i < t; i++) {
            min_angle = min(min_angle, angle(stk[i], stk[i - 1], stk[i + 1]));
        }
        printf("Case %d: %.6lf\n", ++kase, min_angle * 180.0 / pi);
    }
    return 0;
}