Feedforward and BackPropagation Algorithm
在下图所示的Neural Network中,我们将拥有三个节点的layer1及layer4分别称为输入和输出层,而中间的两层layer2,layer3称为隐藏层(hidden layer)。输入数据X,从左侧进入神经网络,经过层层传播最终从右侧输出的过程,称为Feedforward。而根据training set来调整参数的算法,称为Backpropagation Algorithm,即反向传播算法。

在Hidden layer的每个Node中,都存在一个non-linear unit,常用的是有tanh,sigmoid以及ReLu等。如果没有non-linear unit,则无论NN的architecture如何,输出将永远是输入数据的线性组合,Neural Network也就失去了意义。
首先我们约定weight的表达方式如下图所示:

每个节点的左侧输入值z等于:

每个节点的右侧输出值a等于在其输入值z的基础上,施加非线性可微函数σ

假设Neural Network总共有L层,则会有L-1个ω矩阵存在,所以ω矩阵的维度是size(ω)=q*p,其中q为下一层的节点数,p为本层的节点数。在上图的Layer3中,w3为如下的2x4的矩阵形式:

如果将Feedforward propagation的过程矩阵化,则可以写为:

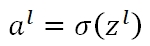
下面来看如何使用Backpropagation更新ω呢。Backpropagation其实是Gradient Descent的一种拓展,如果我们能够拿到cost function对某个ω的梯度值,那么我们就可以对其做梯度下降并迭代求出最优结果。更新算法见:线性回归与梯度下降
为了说明方便,一般会定义一个δ作为某一个节点输入端的误差(即z值的误差):

矩阵化后:
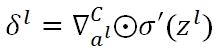
我们可以根据上式,直接算出最后一层的δ值,但是对于任意一层、任意一个节点的δ,则需要将最后一层的误差值进行层层传导,其公式为:
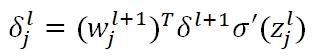
矩阵化后,任意一层的节点误差矩阵为
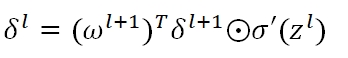
而我们最终的目的在于求得w的梯度,从而利用gradient descent去更新参数,对于任意一层l的某条路径j,k,我们有:

对任意一层l的所有weight,我们有:
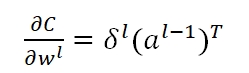
对于第l层bias处的梯度:
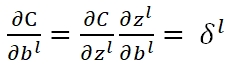
Feedforward and BackPropagation Algorithm的更多相关文章
- CheeseZH: Stanford University: Machine Learning Ex4:Training Neural Network(Backpropagation Algorithm)
1. Feedforward and cost function; 2.Regularized cost function: 3.Sigmoid gradient The gradient for t ...
- BP反向传播算法的工作原理How the backpropagation algorithm works
In the last chapter we saw how neural networks can learn their weights and biases using the gradient ...
- 反向传播算法 Backpropagation Algorithm
假设我们有一个固定样本集,它包含 个样例.我们可以用批量梯度下降法来求解神经网络.具体来讲,对于单个样例(x,y),其代价函数为:这是一个(二分之一的)方差代价函数.给定一个包含 个样例的数据集,我们 ...
- The Backpropagation Algorithm
https://page.mi.fu-berlin.de/rojas/neural/chapter/K7.pdf 7.1 Learning as gradient descent We saw in ...
- 神经网络(9)--如何求参数: backpropagation algorithm(反向传播算法)
Backpropagation algorithm(反向传播算法) Θij(l) is a real number. Forward propagation 上图是给出一个training examp ...
- [Converge] Backpropagation Algorithm
Ref: CS231n Winter 2016: Lecture 4: Backpropagation Ref: How to implement a NN:中文翻译版本 Ref: Jacobian矩 ...
- 一文弄懂神经网络中的反向传播法(Backpropagation algorithm)
最近在看深度学习的东西,一开始看的吴恩达的UFLDL教程,有中文版就直接看了,后来发现有些地方总是不是很明确,又去看英文版,然后又找了些资料看,才发现,中文版的译者在翻译的时候会对省略的公式推导过程进 ...
- (六) 6.2 Neurons Networks Backpropagation Algorithm
今天得主题是BP算法.大规模的神经网络可以使用batch gradient descent算法求解,也可以使用 stochastic gradient descent 算法,求解的关键问题在于求得每层 ...
- 吴恩达机器学习笔记30-神经网络的反向传播算法(Backpropagation Algorithm)
之前我们在计算神经网络预测结果的时候我们采用了一种正向传播方法,我们从第一层开始正向一层一层进行计算,直到最后一层的ℎ
随机推荐
- [BZOJ 3110] [luogu 3332] [ZJOI 2013]k大数查询(权值线段树套线段树)
[BZOJ 3110] [luogu 3332] [ZJOI 2013]k大数查询(权值线段树套线段树) 题面 原题面有点歧义,不过从样例可以看出来真正的意思 有n个位置,每个位置可以看做一个集合. ...
- Python的__pycache__的文件夹
· 前言 用python编写好一个工程,在第一次运行后,总会发现工程根目录下生成了一个__pycache__文件夹,里面是和py文件同名的各种 *.pyc 或者 *.pyo 文件. 先大概了解一下py ...
- React中state和props分别是什么?
整理一下React中关于state和props的知识点. 在任何应用中,数据都是必不可少的.我们需要直接的改变页面上一块的区域来使得视图的刷新,或者间接地改变其他地方的数据.React的数据是自顶向下 ...
- UI标签库专题十:JEECG智能开发平台 Form(form标签)
版权声明:本文为博主原创文章,未经博主同意不得转载. https://blog.csdn.net/zhangdaiscott/article/details/30099121 1. Form(f ...
- Rabbitmq 运维
Rabbitmq 运维 一.安装: 安装ncurses wget http://ftp.gnu.org/gnu/ncurses/ncurses-6.1.tar.gz tar zxf ncurses-6 ...
- ionic -v2版本项目结构
myApp │ config.xml //项目配置文件,包名.名称.minSdkVersion等都在此处配置 │ ionic.config.json │ package.json //项目依 ...
- Latex--入门系列一
Latex 专业的参考 tex对于论文写作或者其他的一些需要排版的写作来说,还是非常有意义的.我在网上看到这个对于Latex的入门介绍还是比较全面的,Arbitrary reference .所以将会 ...
- Node.JS-经典教程
目录 1. 下载地址 2. 目录 1. 下载地址 https://www.cnblogs.com/coco56/p/11223189.html 在视频教程那里 2. 目录 00课件.rar 01.历史 ...
- linux grep 设置高亮显示
[root@eric ~]# vi /etc/profile alias grep='grep --color=auto' [root@eric ~]# source /etc/profile
- C++中的const_cast
开发环境 Qt Creator 4.8.2 编译器版本 MinGw 32-bit const_cast 用法: const_cast<type_id> (expression) 说明: 该 ...
