Codeforces 396C (DFS序+线段树)

题面

传送门

题目大意:

给定一棵树,每个点都有权值,边的长度均为1,有两种操作

操作1:将节点u的值增加x,并且对于u的子树中的任意一个点v,将它的值增加x-dist(u,v)*k, dist(u,v)表示u,v之间的距离

操作2:查询节点u的值

分析

这类题目需要用到一个重要的思想:将树上操作转化为区间操作

通过DFS序我们可以实现这一点.

对于每个节点x,我们记录它在前序遍历中的位置l[x],再一次回到x时的序号r[x],则x及其子树的区间为前序遍历中的[l[x],r[x]]

如:



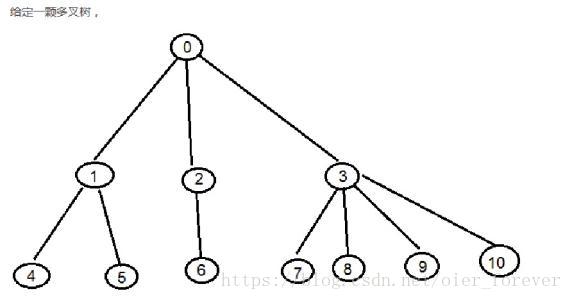
这棵树的前序遍历为0 1 4 5 2 6 3 7 8 9 10

后序遍历为4 5 1 6 2 7 8 9 10 3 0

对于点3来说,它在前序遍历中的序号为7,遍历完7,8,9后回到3的序号为10,则区间为[7,10]

将树上操作转化为区间之后,我们处理两种操作

显然是用线段树的区间修改和单点查询实现

每次修改时,对于u的后代v,我们发现它增加的值=x+k(d[v]−d[u])=x+k×d[u]−k×d[v]" role="presentation" style="position: relative;">=x+k(d[v]−d[u])=x+k×d[u]−k×d[v]=x+k(d[v]−d[u])=x+k×d[u]−k×d[v] (d[x]表示x的深度)

其中,对于u的每个后代v,x+k×d[u]" role="presentation" style="position: relative;">x+k×d[u]x+k×d[u]都是一样的,可以批量修改,而k×d[v]" role="presentation" style="position: relative;">k×d[v]k×d[v]则由每个节点决定

因此,我们用两棵线段树维护

一棵维护x+k×d[u]" role="presentation" style="position: relative;">x+k×d[u]x+k×d[u],一棵维护k" role="presentation" style="position: relative;">kk

修改时,我们把x+k×d[u]" role="presentation" style="position: relative;">x+k×d[u]x+k×d[u]和k" role="presentation" style="position: relative;">kk分别累加到区间[l[u],r[u]]中每一个点

查询时,我们可以求出每个节点的x+k×d[u]" role="presentation" style="position: relative;">x+k×d[u]x+k×d[u]的总和a,以及k" role="presentation" style="position: relative;">kk的总和b

答案就是a−b∗d[u]" role="presentation" style="position: relative;">a−b∗d[u]a−b∗d[u]

时间复杂度O(n+qlog2n)" role="presentation" style="position: relative;">O(n+qlog2n)O(n+qlog2n)

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#define maxn 300005
#define mod 1000000007ll
using namespace std;
int n,q;
struct edge{
    int from;
    int to;
    int next;
}E[maxn<<1];
int size;
int head[maxn];
void add_edge(int u,int v){
    size++;
    E[size].from=u;
    E[size].to=v;
    E[size].next=head[u];
    head[u]=size;
}

struct segment_tree{
    struct node{
        int l;
        int r;
        long long mark;
        long long v;
    }tree[maxn<<2];
    segment_tree(){
        memset(tree,0,sizeof(tree));
    }
    void build(int l,int r,int pos){
        tree[pos].l=l;
        tree[pos].r=r;
        tree[pos].mark=0;
        tree[pos].v=0;
        if(l==r) return;
        int mid=(l+r)>>1;
        build(l,mid,pos<<1);
        build(mid+1,r,pos<<1|1);
    }
    void push_down(int pos){
        if(tree[pos].mark){
            tree[pos<<1].mark=(tree[pos].mark+tree[pos<<1].mark)%mod;
            tree[pos<<1|1].mark=(tree[pos].mark+tree[pos<<1|1].mark)%mod;
            tree[pos<<1].v=(tree[pos].mark+tree[pos<<1].v)%mod;
            tree[pos<<1|1].v=(tree[pos].mark+tree[pos<<1|1].v)%mod;
            tree[pos].mark=0;
        }
    }
    void update(int L,int R,long long v,int pos){
        if(L<=tree[pos].l&&R>=tree[pos].r){
            tree[pos].v=(tree[pos].v+v)%mod;
            tree[pos].mark=(tree[pos].mark+v)%mod;
            return ;
        }
        push_down(pos);
        int mid=(tree[pos].l+tree[pos].r)>>1;
        if(L<=mid) update(L,R,v,pos<<1);
        if(R>mid) update(L,R,v,pos<<1|1);
        return;
    }
    long long query(int L,int R,int pos){
        if(L<=tree[pos].l&&R>=tree[pos].r){
            return tree[pos].v;
        }
        push_down(pos);
        int mid=(tree[pos].l+tree[pos].r)>>1;
        long long ans=0;
        if(L<=mid) ans=(ans+query(L,R,pos<<1))%mod;
        if(R>mid) ans=(ans+query(L,R,pos<<1|1))%mod;
        return ans;
    }
};
segment_tree T1,T2;
int l[maxn],r[maxn];
int deep[maxn];
int cnt=0;
void dfs(int x,int fa){
    l[x]=++cnt;
    deep[x]=deep[fa]+1;
    for(int i=head[x];i;i=E[i].next){
        int y=E[i].to;
        if(y!=fa){
            dfs(y,x);
        }
    }
    r[x]=cnt;
}
int main(){
    int p,cmd;
    int v,x,k;
    scanf("%d",&n);
    int root;
    for(int i=2;i<=n;i++){
        scanf("%d",&p);
            add_edge(i,p);
            add_edge(p,i);
    }
    dfs(1,0);
    T1.build(1,n,1);
    T2.build(1,n,1);
    scanf("%d",&q);
    for(int i=1;i<=q;i++){
        scanf("%d",&cmd);
        if(cmd==1){
            scanf("%d %d %d",&v,&x,&k);
            T1.update(l[v],r[v],(long long)x+(long long)deep[v]*k%mod,1);
            T2.update(l[v],r[v],(long long)k,1);
        }else{
            scanf("%d",&v);
            long long ans=(T1.query(l[v],l[v],1)-(long long)deep[v]*T2.query(l[v],l[v],1)+mod)%mod;
            if(ans<0) ans+=mod;
            printf("%I64d\n",ans%mod);
        }
    }
}