牛客网NOIP赛前集训营-提高组（第六场） C-树

题目描述

有一棵有 n 个结点的树，每条边有编号为 0,1,2 的三种颜色，刚开始每条边颜色都为 0 。

现在有 3 种操作：

\(1\ x\ y\ col\) ，表示询问 \(x\) 到 \(y\) 的最短路径上有几条颜色为 \(col\) 的边；

\(2\ x\ y\ col_1\ col_2\) ，表示将两个端点都在 \(x\) 到 y 的最短路径上的边的颜色修改为 \(col_1\) ，将恰好有一个端点在 x 到 y 的最短路径上的边的颜色修改为 \(col_2\) ；

\(3\ rt\ x\ col\) ，表示将两个端点都在以 \(rt\) 为根时 \(x\) 的子树里的边的颜色修改为 \(col\) 。

你需要回答每一个询问。

输入描述:

第一行一个整数 n ，表示树的结点个数。

接下来 n-1 行，每行两个整数 x,y，表示在 x 和 y 之间有一条边。点从 1 到 n 编号。

接下来一行一个整数 m ，表示操作个数。

接下来 m 行，第 i 行描述第 i 个操作，格式为题面描述中的三种中的一种。

输出描述:

对于每个询问，输出一行，表示答案。

示例1

输入

5
1 2
2 3
2 4
1 5
5
1 4 5 0
2 3 5 1 2
1 4 5 0
3 2 1 0
1 4 5 0

输出

3
0
1

说明

一开始的树长这样(边上的数字表示其颜色)：

第一个操作是询问 \(4\) 到 \(5\) 的最短路径上有几条边颜色为 \(0\) ，答案为 \(3\) 。

第二个操作是将两个端点都在 \(3,5\) 的最短路径上的边的颜色改为 \(1\) ，恰好有一个端点在路径上的边的颜色改为 \(2\) 。修改后的树长这样：

第三个操作是询问 \(4\) 到 \(5\) 的最短路径上有几条边颜色为 \(0\) ，答案为 \(0\) 。

第四个操作是将两个端点都在以 \(2\) 为根时 \(1\) 的子树的边的颜色修改为 \(0\) 。修改后的树长这样：

第五个操作是询问 \(4\) 到 \(5\) 的最短路径上有几条边颜色为 \(0\) ，答案为 \(1\) 。

说明

全部的输入数据满足：

• $1 \leq n \leq 100000 $
• \(1 \leq m \leq 100000\)
• 修改和询问的颜色都 \(\in\{0,1,2\}\)

各个测试点的性质如下：(若为空，则表示没有特殊性质)

Solution

仔细分析一下，题目中说的三个操作，其中第二个其实可以转化为两个操作，那么就可以用树剖了：

1. 将路径上每个点所有指向儿子的边修改为\(c_2\)

   ​ 这个操作可以另开一个线段树，记录每个点的儿子被修改的情况、同时，对于重孩子，还是要在原线段树上直接修改一下。

2. 将路径上每个点所有指向父亲的边修改为\(c_1\)

   ​ 这个操作直接在原线段树上修改就可以了。

3. 将\(LCA\)的指向父亲的边修改为\(c_2\)

   ​ 这个操作可以与1最后一次修改重孩子时一起完成。

然后其它两个操作。第一个的话，每次直跳重孩子不需要太多考虑。跳轻边的时候，再在另一棵线段树里面查找一下这个点的值与原来的线段树里面的值比较。但是我们无法知道哪一个是现在的值，所以还需要记录一下每一次修改的时间。

至于换根就是套路了。因为如果要真换根，所有什么dfs序，轻重链都会被打乱，所以肯定负担不起。自己画个图，可以发现，如果\(rt\)在原来\(x\)的子树外的时候，换根对x的子树内容没有影响。而如果在\(x\)的子树内的时候，\(x\)的子树全部变成了除了\(rt\)所在的\(x\)的子节点的子树外的所有点。举个例子，下图中，以\(9\)为根\(3\)的子树，就是除了\(7\)在原树种的子树的所有部分。

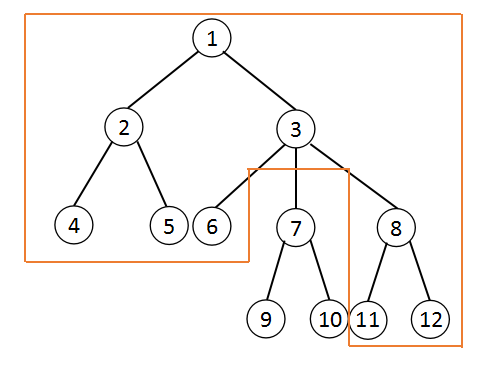
那么这道题目就完整地解决了，下面就是实现的问题了。慢慢写吧，应该是比较裸的数据结构题了。

#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
using namespace std;
#define lowbit(x) ((x)&(-(x)))
#define REP(i,a,n) for(register int i=(a);i<=(n);++i)
#define PER(i,a,n) for(register int i=(a);i>=(n);--i)
#define FEC(i,x) for(register int i=head[x];i;i=g[i].ne)
#define dbg(...) fprintf(stderr,__VA_ARGS__)
#define lc o<<1
#define rc o<<1|1
namespace io{
	const int SIZE=(1<<21)+1;char ibuf[SIZE],*iS,*iT,obuf[SIZE],*oS=obuf,*oT=oS+SIZE-1,c,qu[55];int f,qr;
	#define gc() (iS==iT?(iT=(iS=ibuf)+fread(ibuf,1,SIZE,stdin),(iS==iT?EOF:*iS++)):*iS++)
	inline void flush(){fwrite(obuf,1,oS-obuf,stdout);oS=obuf;}
	inline void putc(char x){*oS++=x;if(oS==oT)flush();}
	template<class I>inline void read(I &x){for(f=1,c=gc();c<'0'||c>'9';c=gc())if(c=='-')f=-1;for(x=0;c<='9'&&c>='0';c=gc())x=x*10+(c&15);x*=f;}
	template<class I>inline void write(I x){if(!x)putc('0');if(x<0)putc('-'),x=-x;while(x)qu[++qr]=x%10+'0',x/=10;while(qr)putc(qu[qr--]);}
	struct Flusher_{~Flusher_(){flush();}}io_flusher_;
}//orz laofudasuan
using io::read;using io::putc;using io::write;
typedef long long ll;typedef unsigned long long ull;
template<typename A,typename B>inline bool SMAX(A&x,const B&y){return y>x?x=y,1:0;}
template<typename A,typename B>inline bool SMIN(A&x,const B&y){return y<x?x=y,1:0;}

const int N=100000+7;
int n,m,opt,x,y,z,z2,T;
int dfc,num[N],son[N],dep[N],f[N],top[N],tree[N],pre[N];
struct Edge{int to,ne;}g[N<<1];int head[N],tot;
inline void Addedge(int x,int y){g[++tot].to=y;g[tot].ne=head[x];head[x]=tot;}

inline void DFS1(int x,int fa=0){
	dep[x]=dep[fa]+1;f[x]=fa;num[x]=1;
	for(register int i=head[x];i;i=g[i].ne){
		int y=g[i].to;if(y==fa)continue;
		DFS1(y,x);num[x]+=num[y];if(num[y]>num[son[x]])son[x]=y;
	}
}
inline void DFS2(int x,int pa){
	top[x]=pa;tree[x]=++dfc;pre[dfc]=x;
	if(!son[x])return;DFS2(son[x],pa);
	for(register int i=head[x];i;i=g[i].ne){
		int y=g[i].to;if(y==f[x]||y==son[x])continue;
		DFS2(y,y);
	}
}

struct Pair{int col,tim;};
struct Node{int s[3],tim;Pair set;}t[N<<2],st[N<<2];
inline void pushup(Node *t,int o,int L,int R){
	if(~t[o].set.col)t[o].tim=t[o].set.tim,t[o].s[0]=t[o].s[1]=t[o].s[2]=0,t[o].s[t[o].set.col]=(R-L+1);
	else t[o].s[0]=t[lc].s[0]+t[rc].s[0],t[o].s[1]=t[lc].s[1]+t[rc].s[1],t[o].s[2]=t[lc].s[2]+t[rc].s[2],t[o].tim=t[lc].tim;
}
inline void pushdown(Node *t,int o,int L,int R){
	if(!~t[o].set.col)return;int M=(L+R)>>1;
	t[lc].set=t[o].set,t[rc].set=t[o].set,t[lc].s[0]=t[lc].s[1]=t[lc].s[2]=t[rc].s[0]=t[rc].s[1]=t[rc].s[2]=0;//错误笔记：把o打成rc。。
	t[lc].s[t[o].set.col]=(M-L+1),t[rc].s[t[o].set.col]=(R-M),t[lc].tim=t[rc].tim=t[o].set.tim;t[o].set.col=-1;
}
inline void Build(Node *t,int o,int L,int R){
	t[o].set={-1,0};t[o].tim=0;if(L==R)t[o].s[0]++;
	else{
		int M=(L+R)>>1;
		Build(t,lc,L,M);Build(t,rc,M+1,R);
		pushup(t,o,L,R);
	}
}
inline void Modify(Node *t,int o,int L,int R,int l,int r,int x){
	if(l<=L&&R<=r)t[o].set={x,T},t[o].s[0]=t[o].s[1]=t[o].s[2]=0,t[o].s[x]=(R-L+1),t[o].tim=T;
	else{
		int M=(L+R)>>1;pushdown(t,o,L,R);
		if(l<=M)Modify(t,lc,L,M,l,r,x);if(r>M)Modify(t,rc,M+1,R,l,r,x);
		pushup(t,o,L,R);
	}
}
inline Pair Ask(Node *t,int o,int L,int R,int l,int r,int x){
	if(l<=L&&R<=r)return Pair{t[o].s[x],t[o].tim};
	else{
		int M=(L+R)>>1,ans=0;Pair p;pushdown(t,o,L,R);
		if(l<=M)ans+=(p=Ask(t,lc,L,M,l,r,x)).col;if(r>M)ans+=(p=Ask(t,rc,M+1,R,l,r,x)).col;
		return Pair{ans,p.tim};
	}
}

inline int QUERY(int x,int y,int c){
	int ans=0;
	while(top[x]!=top[y]){
		if(dep[top[x]]<dep[top[y]])x^=y^=x^=y;
		Pair p,p2,p3=Ask(t,1,1,n,tree[top[x]],tree[top[x]],c);
		if(son[top[x]])p=Ask(t,1,1,n,tree[son[top[x]]],tree[x],c);else p.col=0;
		if(f[top[x]])p2=Ask(st,1,1,n,tree[f[top[x]]],tree[f[top[x]]],c);else p2.tim=-1;
		if(p2.tim<=p3.tim)ans+=p.col+p3.col;else ans+=p.col+p2.col;
		x=f[top[x]];
	}
	if(dep[x]>dep[y])x^=y^=x^=y;
	return ans+=(x!=y?Ask(t,1,1,n,tree[son[x]],tree[y],c).col:0);
}
inline void UPDATE1(int x,int y,int c,int c2){
	++T;while(top[x]!=top[y]){
		if(dep[top[x]]<dep[top[y]])x^=y^=x^=y;
		Modify(t,1,1,n,tree[top[x]],tree[x],c);
		x=f[top[x]];
	}
	if(dep[x]>dep[y])x^=y^=x^=y;
	x!=y?Modify(t,1,1,n,tree[son[x]],tree[y],c):(void)0;
}
inline void UPDATE2(int x,int y,int c){
	++T;while(top[x]!=top[y]){
		if(dep[top[x]]<dep[top[y]])x^=y^=x^=y;
		Modify(st,1,1,n,tree[top[x]],tree[x],c);if(son[top[x]])Modify(t,1,1,n,tree[son[top[x]]],son[x]?tree[son[x]]:tree[x],c);
		x=f[top[x]];
	}
	if(dep[x]>dep[y])x^=y^=x^=y;
	Modify(st,1,1,n,tree[x],tree[y],c);Modify(t,1,1,n,tree[x],son[y]?tree[son[y]]:tree[y],c);
}
inline int Get_Son(int x,int y){
	int ans=0;
	while(top[x]!=top[y])y=f[ans=top[y]];
	if(x==y)return ans;else return son[x];
}
inline void UPDATE3(int rt,int x,int c){
	++T;if(x==rt)Modify(t,1,1,n,1,n,c);
	else if(tree[rt]<tree[x]||tree[rt]>tree[x]+num[x]-1)Modify(t,1,1,n,tree[x]+1,tree[x]+num[x]-1,c);
	else{
		int y=Get_Son(x,rt);
		if(tree[y]>1)Modify(t,1,1,n,1,tree[y]-1,c);if(tree[y]+num[y]<=n)Modify(t,1,1,n,tree[y]+num[y],n,c);
	}
}

int main(){
#ifndef ONLINE_JUDGE
	freopen("C.in","r",stdin);freopen("C.out","w",stdout);
#endif
	read(n);
	for(register int i=1;i<n;++i)read(x),read(y),Addedge(x,y),Addedge(y,x);
	DFS1(1);DFS2(1,1);Build(t,1,1,n);Build(st,1,1,n);
	read(m);for(register int i=1;i<=m;++i){
		read(opt),read(x),read(y),read(z);if(opt==2)read(z2);
		if(opt==1)write(QUERY(x,y,z)),putc('\n');else if(opt==2){UPDATE2(x,y,z2);UPDATE1(x,y,z,z2);}
		else UPDATE3(x,y,z);
	}
}