Codeforces 932 E Team Work ( 第二类斯特林数、下降阶乘幂、组合数学 )

题目链接

题意 : 其实就是要求

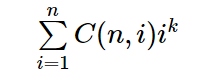
分析 :

先暴力将次方通过第二类斯特林数转化成下降幂 ( 套路？)

然后再一步步化简、使得最外层和 N 有关的 ∑ 划掉

这里有个技巧就是

将组合数的表达式放到一边、然后通过组合意义来化简

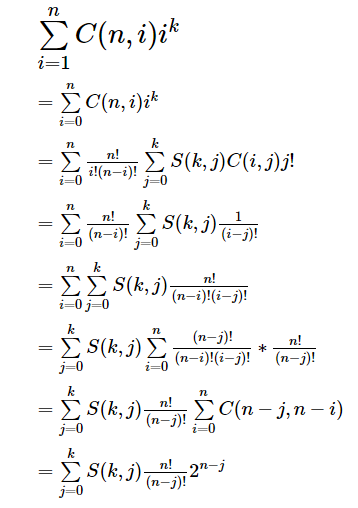
然后就可以 O( k ^ 2 ) 算出答案了

另外化到后面其实有种产生

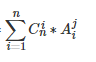
这里可以用另外一种方式化简

考虑其组合意义

相当于先从 n 个数中挑出 i 个数、然后再从 i 个数中取 j 个进行排列

其他数可选可不选

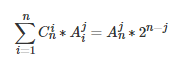
具体可以看 Click here

#include<bits/stdc++.h>
#define LL long long
#define ULL unsigned long long

#define scs(i) scanf("%s", i)
#define sci(i) scanf("%d", &i)
#define scd(i) scanf("%lf", &i)
#define scIl(i) scanf("%I64d", &i)
#define scii(i, j) scanf("%d %d", &i, &j)
#define scdd(i, j) scanf("%lf %lf", &i, &j)
#define scIll(i, j) scanf("%I64d %I64d", &i, &j)
#define sciii(i, j, k) scanf("%d %d %d", &i, &j, &k)
#define scddd(i, j, k) scanf("%lf %lf %lf", &i, &j, &k)
#define scIlll(i, j, k) scanf("%I64d %I64d %I64d", &i, &j, &k)
#define sciiii(i, j, k, l) scanf("%d %d %d %d", &i, &j, &k, &l)
#define scdddd(i, j, k, l) scanf("%lf %lf %lf %lf", &i, &j, &k, &l)
#define scIllll(i, j, k, l) scanf("%I64d %I64d %I64d %I64d", &i, &j, &k, &l)

#define lson l, m, rt<<1
#define rson m+1, r, rt<<1|1
#define lowbit(i) (i & (-i))
#define mem(i, j) memset(i, j, sizeof(i))

#define fir first
#define sec second
#define VI vector<int>
#define ins(i) insert(i)
#define pb(i) push_back(i)
#define pii pair<int, int>
#define VL vector<long long>
#define mk(i, j) make_pair(i, j)
#define all(i) i.begin(), i.end()
#define pll pair<long long, long long>

#define _TIME 0
#define _INPUT 0
#define _OUTPUT 0
clock_t START, END;
void __stTIME();
void __enTIME();
void __IOPUT();
using namespace std;
;
;

LL S[maxn][maxn];

inline void init()
{
    S[][] = ;
    ; i<maxn; i++){
        ; j<=i; j++){
            S[i][j] = ( S[i-][j-] + (LL)j * S[i-][j] % mod ) % mod;
        }
    }
}

LL pow_mod(LL a, LL b)
{
    a %= mod;
    LL ret = ;
    while(b){
        ) ret = ret * a % mod;
        a = a * a % mod;
        b >>= ;
    }return ret;
}

int main(void){__stTIME();__IOPUT();

    init();

    LL n, k;

    scIll(n, k);

    LL ans = ;
    LL fac = ;
    ; j<=min(n, k); j++){
        ans = (ans + ( (S[k][j] * fac % mod) * pow_mod(, n-j) ) %mod) % mod;
        fac = fac * (n-j) % mod;
    }

    ) ans--;

    printf("%I64d\n", ans);

__enTIME();;}

void __stTIME()
{
    #if _TIME
        START = clock();
    #endif
}

void __enTIME()
{
    #if _TIME
        END = clock();
        cerr<<"execute time = "<<(double)(END-START)/CLOCKS_PER_SEC<<endl;
    #endif
}

void __IOPUT()
{
    #if _INPUT
        freopen("in.txt", "r", stdin);
    #endif
    #if _OUTPUT
        freopen("out.txt", "w", stdout);
    #endif
}