Kruskal 重构树小记

其实也不是多难的知识点吧……学了一个中午+半个下午就把它学会了（做过那道 jxd 作业 CF571D 的应该比较好理解）

Kruskal 重构树大概就是在正常 Kruskal 的时候，对于两个需要连边的点 \(u,v\) 不直接连边，而是新增一个虚拟节点 \(T\)，权值为 \(u,v\) 间的边权 \(w\)，并连边 \(T\to u,T\to v\)。

下图可以较为清楚地展示 Kruskal 重构树的过程，正常的 Kruskal 我们是这样连边的：

而 Kruskal 重构树我们是这样连边的：

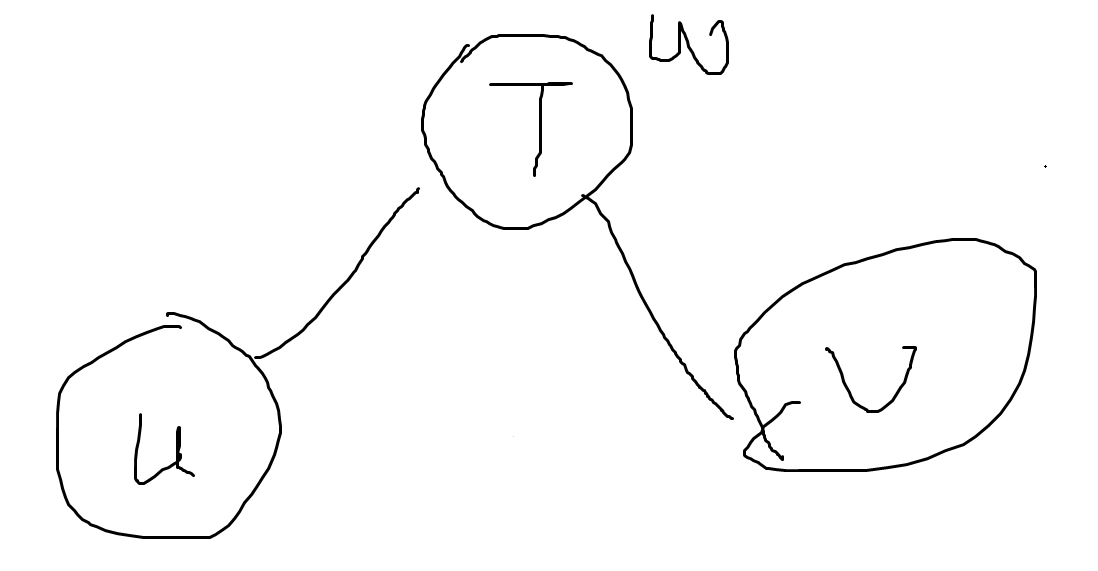
显然这样建出来的图是一棵树，而这棵树有以下性质：

由于我们每个新建的点都恰好连出的两条边，因此这棵树是一个二叉树
由于我们是按照边权从小到大排序来建树的，因此这棵树的权值可以看作一个大根堆（假设叶子节点的权值为 \(0\) 或 \(-\infty\)）
对于两个点 \(u,v\)，它们之间路径最大值的最小值就是 Kruskal 重构树上它们 LCA 的权值，这个用普通的 Kruskal 建出最小生成树再查询它们之间路径权值最大值的方法也可说明
对于一个点 \(u\)，记 \(v\) 为离 \(u\) 最远的满足 \(v\) 的权值 \(\le w\) 的 \(u\) 的祖先，那么所有 \(u\) 经过权值 \(\le w\) 的边能够到达的点的集合恰好为 \(v\) 子树内所有叶子节点，这个性质相当重要，因为它可以将我们陌生的图的连通性问题转化为熟悉的子树问题，而这恰恰是可以通过 DFS 序套上某些数据结构维护的。

Kruskal 重构树的知识点就这么多，实现起来不算太难，只不过有以下需要注意的地方：

Kruskal 重构树点数最多会达到 \(2n-1\)，因此要开两倍空间
如果题目图不连通，那么最后建出的 Kruskal 重构树也不连通，也就是说最后得到的是一个二叉森林，此时就要额外补上一个节点 \(R\)，权值为 \(\infty\)，并将 \(R\) 与森林中所有连通块的根节点之间连边（当然这样得到的树就不是二叉树了）

代码想想还是贴一下罢（当然这是题目保证连通的情况的代码，如果题目没保证连通那后面还要加上两三句话，由于过于简单就不贴了）：

int hd[MAXN*2+5],nxt[MAXN*2+5],to[MAXN*2+5],ec=0;

void adde(int u,int v){to[++ec]=v;nxt[ec]=hd[u];hd[u]=ec;}

int f[MAXN*2+5],nc;

int main(){

    nc=n;for(int i=1;i<=n;i++) f[i]=i;

	for(int i=1,u,v;i<=m;i++){

		u=find(u);v=find(v);if(u==v) continue;++nc;

        f[u]=f[v]=f[nc]=nc;adde(nc,u);adde(nc,v);val[nc]=i;

	}

}

总之，Kruskal 重构树无法解决权值之和最小的问题，它只能解决路径上权值最大值最小或最小值最大的可达性问题，因此看到类似于”只经过权值 \(\le w\) 的边“或者”能够到达的点当中“等字眼就可以联想到 Kruskal 重构树。

例题：

1. AT1998 [AGC002D] Stamp Rally

差点不会做，身败名裂

首先以边的编号为权值建出 Kruskal 重构树，对每个询问考虑二分，二分答案 \(mid\)，那么显然可以倍增找出 \(x\) 可以到达的点和 \(y\) 可以到达的点，显然是两个子树 \(u\) 和 \(v\) 的并，而这个并的大小可用通过判断 \(u,v\) 是否存在祖先关系求出，如果存在就是祖先子树大小，否则就是 \(siz_u+siz_v\)，将它与 \(z\) 比较即可。

时间复杂度 \(n\log^2n\)，可能有 \(n\log n\) 的做法，不过估计 Kruskal 重构树是做不了了（

u1s1 倍增是真的喜欢和 Kruskal 重构树贴贴（大雾

2. P4197 Peaks

还是建出 Kruskal 重构树，倍增找出对应子树 \(u\)，然后建立主席树，在主席树上离散化+二分找第 \(k\) 大即可。

时间复杂度 \(n\log n\)。

好套路啊……

3. CF1416D Graph and Queries

考虑离线，对每条边记它的边权为它被删除的时间（如果没被删除则为 \(q+1\)），然后建 Kruskal 重构树（这次要建个大根堆，因为可以访问的边的边权要大于某个数），然后对每个询问还是倍增找出它可以到达的点，然后线段树+DFS 序找出子树内权值最大的点赋为 \(0\) 即可。

时间复杂度 \(n\log n\)。

4. P4768 [NOI2018] 归程

首先最优方案肯定是开一段距离的车然后走一段距离，而由于终点都是 \(1\) 且图为无向图，因此可以 dijkstra（关于 S P F A，它死了，死于这道题的手中）求出 \(1\) 到每个点的最短距离 \(dis_i\)，那么每个询问的答案就是 \(v\) 能到达的点中 \(dis\) 的最小值，这个显然是可以 Kruskal 重构树解决的，而且甚至不用什么数据结构（不愧是你 NOI 签到题），直接记录一个子树最小值即可。

时间复杂度 \(Tn\log n\)。

5. P4899 [IOI2018] werewolf 狼人

我竟然能独立想出来近几年 IOI 的题，incredible！

首先题目等价于能否找到一个编号在 \([L_i,R_i]\) 之间的点 \(t\)，满足存在 \(U_i\to t\)，只经过编号 \(\ge L_i\) 的点的路径，也存在 \(t\to V_i\)，只经过编号 \(\le R_i\) 的路径。

这东西显然是可以 Kruskal 重构树的，比较棘手的一点是此题涉及点权，而不是边权。不过事实上转化非常容易，显然对于一条边 \((u,v)\) 而言，只有 \(u,v\) 的权值都符合要求，\((u,v)\) 才能通过，那么我们就可以把 \((u,v)\) 的权值设为 \(\min(w_u,w_v)\)（如果要求经过的边权值 \(\ge v\)）或者 \(\max(w_u,w_v)\)（如果要求经过的边权值 \(\le v\)），这样就可以 Kruskal 重构树了。

于是现在题目转化为，对于有两棵树，\(q\) 组询问，每组询问给出第一棵树上的点 \(u\) 和第二棵树上的点 \(v\)，判断是否存在一个叶子节点在 \(u,v\) 的子树中，这个可以使用 DFS 序转化为区间问题，然后就可以主席树维护了，有点类似于这个题，时间复杂度 \(n\log n\)