BST的中序后继

二叉搜索树中的顺序后继：从BST中找到指定节点的下一个节点。



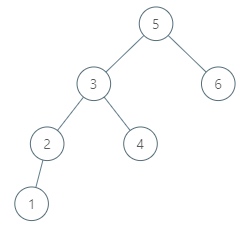
比如1的下一个是2，2的下一个是3，4的下一个是5.

思路：

方法1：递归执行中序遍历，获取list，得到p的下一个。时间O(N)，空间O(N)

方法2：

递归执行中序遍历，在递归过程中获取x的下一个。如果当前值是<=x的，那么根据BST的特性只需要在右子树中找。如果当前值>x，则当前值有可能，它的左子树也有可能有更小的但是也>x的，对左子递归后，选择更接近的（更小的).

时间O(logN)，空间O(logN)调用栈的深度。

public TreeNode inorderSuccessor(TreeNode root, TreeNode p) {
    if(p==null||root==null){
        return null;
    }
    if(root.val<=p.val){//当前和左边都不可能>p
        return inorderSuccessor(root.right,p);
    }
    //root>p
    TreeNode res1=inorderSuccessor(root.left,p);
    if(res1!=null&&res1.val<root.val){
        return res1;
    }else{
        return root;
    }
}

方法3：循环实现

如果当前值是<=x的，那么根据BST的特性只需要在右子树中找：cur=cur.right。

如果当前值>x，则当前值有可能，它的左子树也有可能有更小的但是也>x的。则每次走入这个分支时，当前点是一个候选点，记录该节点的值和历史最小节点的值。

时间O(logN)，空间O(1）

public TreeNode inorderSuccessor(TreeNode root, TreeNode p) {
    if(p==null||root==null){
        return null;
    }
    TreeNode cur=root;
    TreeNode res=null;
    while(cur!=null){
        if(cur.val<=p.val){
            cur=cur.right;
        }else{
            if(res==null||res.val>cur.val){
                res=cur;
            }
            cur=cur.left;
        }
    }
    return res;
}

二叉搜索树中的中序后继 II，这道题和上面一道题是一样的，唯一的区别是节点并非普通的二叉树节点，还带有父节点指针。

循环实现：分析得出：

1. 如果有右子树：则后继节点是右子的最左值。
2. 否则，向上找。cur作为左子时，对于的父节点是第一个>x的值。

public Node inorderSuccessor(Node x) {
    if(x==null){
        return null;
    }
    if(x.right!=null){
        Node tmp=x.right;
        while(tmp.left!=null){
            tmp=tmp.left;
        }
        return tmp;
    }else{
        Node cur=x;
        while(cur.parent!=null&&cur!=cur.parent.left){
            cur=cur.parent;
        }
        //cur为null、cur的parent为null
        return cur.parent;
    }
}