2020.5.4-ICPC Pacific Northwest Regional Contest 2019

A. Radio Prize

All boring tree-shaped lands are alike, while all exciting tree-shaped lands are exciting in their own special ways.What makes Treeland more exciting than the other tree-shaped lands are the raddest radio hosts in the local area: Rootand Leaf. Every morning on FM 32:33 (repeating of course), Root and Leaf of The Full Depth Morning Show serveup the hottest celebrity gossip and traffic updates.

The region of Treeland is made of nn cities, connected by n - 1n−1 roads such that between every pair of cities there isexactly one simple path. The iith road connects cities u_iui​ and v_ivi​, and has a toll of w_iwi​.

To reward their loyal listeners, The Full Depth Morning Show is giving away a number of travel packages! Root andLeaf will choose n - 1n−1 lucky residents from the city that sends them the most fan mail. Each of those residents thengets a distinct ticket to a different city in Treeland.

Each city in Treeland has its own tax on prizes: t_iti​. Let d_{u,v}du,v​be the sum of the tolls on each road on the only simplepath from city uu to vv. For a trip from city uu to city vv, the cost of that trip is then (t_u + t_v)d_{u,v}(tu​+tv​)du,v​.

The shock jocks haven’t quite thought through how much their prize is worth. They need to prepare a report to theradio executives, to summarize the expected costs. For each city that could win the prize, what is the total cost ofpurchasing all the tickets?

input

The first line of input is a single integer n (1 \leq≤ n \leq≤ 100 000). The next line has nnspace-separated integers t_iti​(1 \leq t_i \leq 1 0001≤ti​≤1000), the tax in each city. The following n - 1n−1 lines each have 3 integers, u_i,v_i,w_iui​,vi​,wi​, meaning the iith roadconnects cities u_iui​ and v_ivi​(1 \leq u_i,v_i \leq n1≤ui​,vi​≤n), with a toll of w_iwi​ (1 \leq w_i \leq 1 0001≤wi​≤1000).

output

Output nn lines. On the iith line, output a single integer: the cost of purchasing tickets if city i wins the contest

样例输入

5

2 5 3 4 1
1 2 2
2 4 5
4 3 3
5 2 6

样例输出

1

130
159
191
163
171

样例输入2复制

6
4 3 3 4 3 3
1 3 2
2 1 1
1 4 6
4 5 6
6 4 2

样例输出2复制

209
206
232
209
336
232

#include <iostream>
#include <iomanip>
#include <algorithm>
#include <vector>
#include <utility>

using namespace std;

using ll = long long;
using pii = pair<int, int>;

constexpr int MAXN = 100000;
int n;
int t[MAXN];
vector<pii> tree[MAXN];

int depth[MAXN];
int sz[MAXN];
ll tsum[MAXN];
ll ans[MAXN];

void dfs1(int u, int p) {
    sz[u] = 1;
    tsum[u] = t[u];
    for (auto& e : tree[u]) {
        int v, w;
        tie(v, w) = e;

        if (v == p) continue;

        depth[v] = depth[u] + w;

        dfs1(v, u);

        sz[u] += sz[v];
        tsum[u] += tsum[v];
    }
}

void dfs2(int u, int p, ll depth_sum, ll tax_depth_sum) {
    ans[u] = t[u] * depth_sum + tax_depth_sum;
    for (auto& e : tree[u]) {
        int v, w;
        tie(v, w) = e;
        if (v == p) continue;

        dfs2(
            v,
            u,
            depth_sum + w * (n - 2 * sz[v]),
            tax_depth_sum + w * (tsum[0] - 2 * tsum[v])
        );
    }
}

int main() {
    cin >> n;

    for (int i = 0; i < n; ++i) {
        cin >> t[i];
    }

    for (int i = 1; i < n; ++i) {
        int u, v, w;
        cin >> u >> v >> w;
        --u; --v;
        tree[u].emplace_back(v, w);
        tree[v].emplace_back(u, w);
    }

    dfs1(0, -1);
    ll depth_sum = 0;
    ll tax_depth_sum = 0;
    for (int i = 0; i < n; ++i) {
        depth_sum += depth[i];
        tax_depth_sum += 1LL * t[i] * depth[i];
    }

    dfs2(0, -1, depth_sum, tax_depth_sum);

    for (int i = 0; i < n; ++i) {
        cout << ans[i] << '\n';
    }

    return 0;
}

B. Perfect Flush

You are given a list of integers x_1,x_2,\ldots,x_nx1​,x2​,…,xn​ and a number kk. It is guaranteed that each i from 1 to k appears in thelist at least once.Find the lexicographically smallest subsequence of x that contains each integer from 1 to k exactly once.

input

The first line will contain two integers nn and kk, with 1 \leq k \leq n \leq 200 0001≤k≤n≤200000. The following n lines will each containan integer x_ixi​ with 1 \leq x_i \leq k1≤xi​≤k.

output

Write out on one line, separated by spaces, the lexicographically smallest subsequence of x that has each integer from 1 to k exactly once

样例输入1复制

6 3
3
2
1
3
1
3

样例输出1复制

2 1 3

样例输入2复制

10 5
5
4
3
2
1
4
1
1
5
5

样例输出2复制

3 2 1 4 5

#include <iostream>
#include <map>
#include <vector>
using namespace std ;
int main() {
   int n, k ;
   cin >> n >> k ;
   vector<int> v(n) ;
   for (auto &a : v) {
      cin >> a ;
      a-- ;
   }
   vector<int> r ;
   vector<char> seen(k) ;
   vector<int> nextlast(n) ;
   vector<int> next(n) ;
   vector<int> nextlink(k) ;
   for (auto &e : nextlink)
      e = -1 ;
   for (int i=n-1; i>=0; i--) {
      int e = v[i] ;
      next[i] = nextlink[e] ;
      nextlink[e] = i ;
   }
   int st = 0 ;
   int need = k ;
   int at = n ;
   int ptr = n ;
   while (need > 0 && at > 0) {
      at-- ;
      if (seen[v[at]] == 0) {
         nextlast[at] = ptr ;
         ptr = at ;
         seen[v[at]] = 2 ;
         need-- ;
      }
   }
   map<int, int> loc ;
   for (int i=0; i<=at; i++)
      if (loc.find(v[i]) == loc.end())
         loc[v[i]] = i ;
   while ((int)r.size() < k) {
      int smi = loc.begin()->second ;
      r.push_back(v[smi]) ;
      seen[v[smi]] = 1 ;
      loc.erase(v[smi]) ;
      while (at < n && seen[v[at]] == 1) {
         int nat = nextlast[at] ;
         for (int i=at+1; i<n && i<=nat; i++)
            if (seen[v[i]] != 1 && loc.find(v[i]) == loc.end())
               loc[v[i]] = i ;
         at = nat ;
      }
      while (st <= smi) {
         if (seen[v[st]] == 2) {
            int nv = next[st] ;
            if (nv >= 0 && nv <= at) {
               loc[v[st]] = nv ;
            } else {
               loc.erase(v[st]) ;
            }
         }
         st++ ;
      }
   }
   for (int i=0; i<(int)r.size(); i++) {
      if (i)
         cout << " " ;
      cout << (1+r[i]) ;
   }
   cout << endl ;
}

C. Coloring Contention

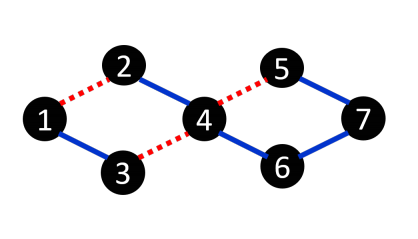
Alice and Bob are playing a game on a simple connected graph with N nodes and M edges.Alice colors each edge in the graph red or blue.A path is a sequence of edges where each pair of consecutive edges have a node in common. If the first edge in thepair is of a different color than the second edge, then that is a “color change.”After Alice colors the graph, Bob chooses a path that begins at node 1 and ends at node N. He can choose any path onthe graph, but he wants to minimize the number of color changes in the path. Alice wants to choose an edge coloringto maximize the number of color changes Bob must make. What is the maximum number of color changes she canforce Bob to make, regardless of which path he chooses?

Input

The first line contains two integer values N and M with 2 \leq N \leq 100 0002≤N≤100000 and 1 \leq M \leq 100 0001≤M≤100000. The next M linescontain two integers a_iai​ and b_ibi​ indicating an undirected edge between nodes a_iai​ and b_ibi​ (1 \leq a_i,b_i \leq N1≤ai​,bi​≤N, a_i \neq b_iai​​=bi​).All edges in the graph are unique.

Output

Output the maximum number of color changes Alice can force Bob to make on his route from node 1 to node N

样例输入1复制

3 3
1 3
1 2
2 3

样例输出1复制

0

样例输入2复制

7 8
1 2
1 3
2 4
3 4
4 5
4 6
5 7
6 7

样例输出2复制

3

// #include <bits/stdc++.h> // this is not C++; this is a Linuxism
#include <iostream>
#include <vector>
#include <queue>

using namespace std;

#define all(x) begin(x), end(x)

using ll = long long;
using ld = long double;
using pii = pair<int, int>;
using vi = vector<int>;

int main() {
    int n, m;
    cin >> n >> m;
    vector<vi> graph(n);
    for (int i = 0; i < m; ++i) {
        int u, v;
        cin >> u >> v;
        --u; --v;

        graph[u].push_back(v);
        graph[v].push_back(u);
    }

    vi dist(n, n + 1);
    dist[0] = 0;
    queue<int> q;
    q.push(0);
    while (!q.empty()) {
        int u = q.front();
        q.pop();
        for (int v : graph[u]) {
            if (dist[v] == n + 1) {
                dist[v] = dist[u] + 1;
                q.push(v);
            }
        }
    }

    cout << dist.back() - 1 << '\n';

    return 0;
}

D. Dividing by Two

You are given two integers, A and B. You want to transform A to B by performing a sequence of operations. You canonly perform the following operations:

• Divide A by two, but only if A is even
• Add one to A.

What is the minimum number of operations you need to transform A into B?

input

The input will be a single line containing two integers A and B with 1 \leq A,B \leq 10^91≤A,B≤109.

output

On a single line write the minimum number of operations required as an integer.

样例输入1复制

103 27

样例输出1复制

4

样例输入2复制

3 8

样例输出2复制

5

#include<bits/stdc++.h>
using namespace std;
int main()
{
    long long n,m,ct;
    while(scanf("%lld%lld",&n,&m)!=EOF)
    {
        ct=0;
        if(n==m)cout<<"0"<<endl;
        else
        {
            if(n<m)
            {
                while(n!=m)
                {
                    n+=1;
                    ct++;
                }
                cout<<ct<<endl;
            }
            else if(n>m)
            {
                    while(n>m)
                    {
                        if(n%2==0)
                      {
                        n/=2;
                        ct++;
                      }
                      else {
                        n+=1;
                        ct++;
                      }
                    }
                      while(n<m) {
                        n+=1;
                        ct++;
                      }
                   cout<<ct<<endl;
                }

        }
    }
}

E. Rainbow Strings

Define a string to be a rainbow string if every letter in the string is distinct. An empty string is also considered a rainbow string.

Given a string of lowercase letters, compute the number of different subsequences which are rainbow strings. Two subsequences are different if an index is included in one subsequence but not the other, even if the resulting strings areidentical.

In the first example, there are 8 subsequences. The only subsequences that aren't rainbow strings are aaaa and aabaab.The remaining 6 subsequences are rainbow strings.

input

The input will consist of a single line with a single string consisting solely of lowercase letters. The length of the stringis between 1 and 100 000 (inclusive).

output

Write on a single line the number of rainbow sequences, modulo the prime 11092019.

样例输入1复制

aab

样例输出1复制

6

样例输入2复制

icpcprogrammingcontest

样例输出2复制

209952

#include <iostream>
#include <vector>
#include <string>
using namespace std ;
typedef long long ll ;
ll MOD = 11092019 ;
int main() {
   string s ;
   cin >> s ;
   vector<int> cnt(256) ;
   for (auto c : s)
      cnt[(int)c]++ ;
   ll r = 1 ;
   for (auto v : cnt)
      r = (r * (v + 1)) % MOD ;
   cout << r << endl ;
}

F. Carny Magician

Charles and Ada are watching a magician shuffling a deck of thirteen numbered cards, which were originally ordered.The magician spreads the cards out on the table.

Ada exclaims, “Odd; ten of the cards are in their original locations!”

Charles thinks for a moment, and says, “Not only that, but it is the forty-second such ordering!”

Can you figure out the order of the cards? Formally, the magician’s cards can be considered as a permutationp_1, p_2, ..., p_np1​,p2​,...,pn​, that contains each number from 1 to nn exactlyexactly once. The number of fixed points is the number ofindices ii such that p_i = ipi​=i.

Given three numbers n, mn,m and kk, find the kkth lexicographically smallest permutation of sizesize nn that has exactly m fixed points.

Input

The input will be a single line containing the three integers n, mn,m, and kk, with 0 ≤ m ≤ n0≤m≤n, 1 ≤ n ≤ 501≤n≤50, and 1 ≤ k ≤ 10^{18}1≤k≤1018.

Output

On a single line, write the permutation as a sequence of nn space-separated integers. If there are fewer than kk permutation satisfying the conditions, then print -1 on a single line.

样例输入1复制

3 1 1

样例输出1复制

1 3 2

样例输入2复制

3 2 1

样例输出2复制

-1

样例输入3复制

5 3 7

样例输出3复制

2 1 3 4 5

G. Glow, Little Pixel, Glow

An LCD panel is composed of a grid of pixels, spaced 11 alu (“arbitrary length unit”) apart both horizontally andvertically. Wires run along each row and each column, intersecting at the pixels. Wires are numbered beginning with 11 and proceeding up to a panel-dependent maximum. The vertical wire numbered 11 lies along the left edge of the panel,and the horizontal wire numbered 11 lies along the bottom edge of the panel.

A pixel will activate, turning dark, when a current is present along both the vertical and horizontal wire passing through that pixel.

For a period of time, we will send pulses of current down selected wires. The current flows down the wires at a speedof one alu per atu (“arbitrary time unit”). The pulses themselves have a length measured in atus. A pixel activates when current is passing through both intersecting wires at the same time. If the leading edge of a pulse on one wirereaches the intersection at the exact same time that the trailing edge of a pulse on the other wire leaves that intersection,the pixel is not activated.

All pulses in vertical wires start from the bottom of the grid. All pulses in horizontal wires start from the left of the grid. At most one pulse will travel along any one wire.

Given the schedule of pulses to be sent through the wires, determine how many pixels will have been activated by the time all pulses have exited the top and right of the grid.

Input

The first line will contain nn, the number of current pulses, with 1 ≤ n ≤ 200 0001≤n≤200000.Following this will be nn lines, each describing a single pulse. Each such line will contain four elements, separated from one another by a single space:

• A single character that is either ‘h’ or ‘v’, indicating the horizontal/vertical direction of the pulse.
• An integer t, 1 ≤ t ≤ 200 0001≤t≤200000, denoting the starting time of the pulse. The starting time is considered to be the moment when the leading edge of a vertical [horizontal] pulse crosses horizontal [vertical] wire #1.
• An integer m, 1 ≤ m ≤ 200 0001≤m≤200000, denoting the length of the pulse.
• An integer aa, 1 ≤ a ≤ 100 0001≤a≤100000, denoting the wire number (horizontal or vertical) along which the pulse willtravel.

Output

Print on a single line the number of pixels that will have activated by the time the last pulse of current has left the grid.

样例输入1复制

4
h 1 4 1
v 2 4 2
h 10 2 2
v 11 2 3

样例输出1复制

2

样例输入2复制

4
h 1 10 1
h 5 10 2
v 1 10 1
v 5 10 3

样例输出2复制

4

样例输入3复制

7
v 1 3 1
v 1 15 2
h 4 5 1
h 5 5 2
h 6 5 3
h 7 5 4
h 8 5 5

样例输出3复制

5

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std ;
typedef long long ll ;
struct traininfo {
   int tim, end ;
   char typ ;
} ;
bool operator<(const traininfo &a, const traininfo &b) {
   if (a.tim != b.tim)
      return a.tim < b.tim ;
   if (a.end != b.end)
      return a.end < b.end ;
   return a.typ < b.typ ;
}
int main() {
   int n ;
   cin >> n ;
   vector<traininfo> sortme ;
   for (int i=0; i<n; i++) {
      char typ ;
      int t0, len, coor ;
      cin >> typ >> t0 >> len >> coor ;
      sortme.push_back({t0-coor, 1, typ}) ;
      sortme.push_back({t0-coor+len, -1, typ}) ;
   }
   sort(sortme.begin(), sortme.end()) ;
   ll rr = 0 ;
   ll hcnt = 0, vcnt = 0 ;
   for (auto v : sortme) {
      if (v.typ == 'h') {
         hcnt += v.end ;
         if (v.end > 0) {
            rr += vcnt ;
         }
      } else {
         vcnt += v.end ;
         if (v.end > 0)
            rr += hcnt ;
      }
   }
   cout << rr << endl ;
}

H. Pivoting Point

Consider a set of points PP in the plane such that no 33 points are collinear. We construct a “windmill” as follows:

Choose a point pp in PP and a starting direction such that the line through pp in that direction does not intersect any otherpoints in PP.Draw that line.

Slowly rotate the line clockwise like a windmill about the point pp as its pivot until the line intersects another point p'p′ in PP. Designate that point p'p′ to be the new pivot (call this “promoting” the point p'p′), and then continue the rotation.

Continue this process until the line has rotated a full 360360 degrees, returning to its original direction (it can be shown that the line will also return to its original position after a 360360 degree rotation).

During this process, a given point can be promoted multiple times. Considering all possible starting pivots and orientations, find the maximum number of times that a single point can be promoted during a single 360360 degree rotation of a line.

Input

The first line of the input will be a single integer nn with 2 ≤ n ≤ 20002≤n≤2000. Following this will be nn lines, each with two integers x_ixi​ and y_iyi​ with -10 000 ≤ xi,yi ≤ 10 000−10000≤xi,yi≤10000.

Output

On one line, write an integer with the largest number of times any particular point can be a pivot when an arbitrarystarting line does a full rotation as described above.

样例输入1复制

3
-1 0
1 0
0 2

样例输出1复制

2

样例输入2复制

6
0 0
5 0
0 5
5 5
1 2
4 2

样例输出2复制

3

#include <iostream>
#include <vector>
using namespace std ;
using ll = long long ;
const ll INF = 2'000'000'000'000'000'000LL ;
ll add(ll a, ll b) {
   ll c = a + b ;
   if (c >= INF)
      return INF ;
   return c ;
}
ll mul(ll a, ll b) {
   if (b > 0 && a > INF / b)
      return INF ;
   return a * b ;
}
const int MAX = 128 ;
ll c[MAX][MAX], f[MAX], g[MAX][MAX] ;
ll g3(ll n, ll m, ll x) {
   return mul(c[x][m], g[n-m][x-m]) ;
}
int main(int argc, char *argv[]) {
   f[0] = 1 ;
   for (int i=1; i<MAX; i++)
      f[i] = mul(f[i-1], i) ;
   for (int i=0; i<MAX; i++) {
      c[i][0] = c[i][i] = 1 ;
      for (int j=1; j<i; j++)
         c[i][j] = add(c[i-1][j-1], c[i-1][j]) ;
   }
   for (int i=0; i<MAX; i++) {
      g[i][0] = f[i] ;
      g[i][1] = mul(i-1, g[i-1][0]) ;
      for (int j=2; j<=i; j++)
         g[i][j] = add(mul(j-1, g[i-1][j-2]), mul(i-j, g[i-1][j-1])) ;
   }
   ll n, p, k ;
   cin >> n >> p >> k ;
   vector<char> used(n) ;
   ll matchable = n ;
   ll thiscnt = 0 ;
   k-- ;
   if (g3(n, p, n) <= k)
      cout << -1 ;
   else
      for (int pos=0; pos<n; pos++) {
         matchable -= !used[pos] ;
         for (int dig=0; dig<n; dig++) {
            if (used[dig])
               continue ;
            if (p == 0 && dig == pos)
               continue ; // no more matches available
            thiscnt = g3(n-pos-1, p-(dig==pos), matchable-(dig>pos)) ;
            if (thiscnt > k) {
               if (pos)
                  cout << " " ;
               cout << (dig + 1) ;
               if (dig > pos)
                  matchable-- ;
               if (dig == pos)
                  p-- ;
               used[dig]++ ;
               break ;
            } else
               k -= thiscnt ;
         }
      }
   cout << endl ;
}

I. Error Correction

You are given WW, a set of NN words that are anagrams of each other. There are no duplicate letters in any word. A setof words S \subseteq WS⊆W is called “swap-free” if there is no way to turn a word x \in Sx∈S into another word y \in Sy∈S by swappingonly a single pair of (not necessarily adjacent) letters in xx. Find the size of the largest swap-free set SS chosen from thegiven set WW.

Input

The first line of input contains an integer NN (1 ≤ N ≤ 5001≤N≤500). Following that are NN lines each with a single word.Every word contains only lowercase English letters and no duplicate letters. All NN words are unique, have at least oneletter, and every word is an anagram of every other word.

Output

Output the size of the largest swap-free set

样例输入1复制

6
abc
acb
cab
cba
bac
bca

样例输出1复制

3

样例输入2复制

11
alerts
alters
artels
estral
laster
ratels
salter
slater
staler
stelar
talers

样例输出2复制

8

样例输入3复制

6
ates
east
eats
etas
sate
teas

样例输出3复制

4

#include <climits>
#include <iostream>
#include <map>
#include <vector>
#include <string>
using namespace std ;
int bc(int v) {
   int r = 0 ;
   while (v) {
      r++ ;
      v &= v-1 ;
   }
   return r ;
}
int calcparity(const string &s) {
   int seen = 0 ;
   int p = 0 ;
   for (auto c : s) {
      c -= 'a' ;
      p += bc(((1<<c)-1) & seen) ;
      seen |= 1<<c ;
   }
   return p&1 ;
}
int diff(const string &a, const string &b) {
   int r = 0 ;
   for (int i=0; i<(int)a.size(); i++)
      r += (a[i] != b[i]) ;
   return r ;
}
struct e {
   int v, flow, c, rev ;
} ;
struct g {
   int v ;
   vector<vector<e>> adj ;
   vector<int> level ;
   g(int v_) : v(v_), adj(v_), level(v_) {}
   void addedge(int a, int b, int c) {
      e ab {b,0,c,(int)adj[b].size()} ;
      e ba {a,0,0,(int)adj[a].size()} ;
      adj[a].push_back(ab) ;
      adj[b].push_back(ba) ;
   }
   int bfs(int s, int t);
   int sendflow(int s, int flow, int t, vector<int> &ptr) ;
   int dinic(int s, int t) ;
} ;
int g::bfs(int s, int t) {
   for (auto &v : level)
      v = -1 ;
   level[s] = 0 ;
   vector<int> q ;
   q.push_back(s) ;
   for (int qg=0; qg<(int)q.size(); qg++) {
      int a = q[qg] ;
      for (auto &e:adj[a])
         if (level[e.v] < 0 && e.flow < e.c) {
            level[e.v] = level[a]+1 ;
            q.push_back(e.v) ;
         }
   }
   return level[t] >= 0 ;
}
int g::sendflow(int a, int flow, int t, vector<int> &start) {
   if (a == t)
      return flow ;
   for (; start[a]<(int)adj[a].size(); start[a]++) {
      e &e = adj[a][start[a]] ;
      if (level[e.v] == level[a]+1 && e.flow < e.c) {
         int curf = min(flow, e.c-e.flow) ;
         int tempf = sendflow(e.v, curf, t, start) ;
         if (tempf > 0) {
            e.flow += tempf ;
            adj[e.v][e.rev].flow -= tempf ;
            return tempf ;
         }
      }
   }
   return 0 ;
}
int g::dinic(int s, int t) {
   if (s == t)
      return -1 ;
   int tot = 0 ;
   vector<int> start(v+1) ;
   while (bfs(s, t)) {
      for (auto &v : start)
         v = 0 ;
      while (int f=sendflow(s, INT_MAX, t, start))
         tot += f ;
   }
   return tot ;
}
int main() {
   int n ;
   cin >> n ;
   vector<string> w(n) ;
   for (auto &v : w)
      cin >> v ;
   vector<int> parity(n) ;
   for (int i=0; i<(int)w.size(); i++)
      parity[i] = calcparity(w[i]) ;
   g graph(n+2) ;
   for (int i=0; i<(int)parity.size(); i++) {
      if (parity[i])
         graph.addedge(i+2, 1, 1) ;
      else {
         graph.addedge(0, i+2, 1) ;
         for (int j=0; j<(int)parity.size(); j++)
            if (parity[j] && diff(w[i], w[j]) == 2)
               graph.addedge(i+2, j+2, 1) ;
      }
   }
   int f = graph.dinic(0, 1) ;
   int r = n - f ;
   cout << r << endl ;
}

J. Interstellar Travel

You are planning to travel in interstellar space in the hope of finding habitable planets. You have already identified NN stars that can recharge your spaceship via its solar panels. The only work left is to decide the orientation of thespaceship that maximizes the distance it can travel.

Space is modeled as a 2D2D plane, with the Earth at the origin. The spaceship can be launched from the Earth in a straight line, in any direction. Star ii can provide enough energy to travel T_iTi​ distance if the spaceship is launched at an angle of a_iai​ with the xx-axis. If the angle is not perfectly aligned, then the spaceship gets less energy. Specifically, if the launch direction makes an angle of aa with the xx-axis, then it gets enough energy to travel distance of

max(0, T_i-s_i * dist(a_i,a))max(0,Ti​−si​∗dist(ai​,a))

from star ii, where dist(a, b)dist(a,b) is the minimum radians needed to go from angle aa to bb. The distance that the spaceship can travel is simply the sum of the distances that each star contributes. Find the maximum distance TT that the star ship can travel.

Input

The first line contains the value NN, 1 ≤ N ≤ 10^51≤N≤105. Following this are NN lines each containing three real numbers T_iTi​,s_isi​, and a_iai​, with 0 < T_i ≤ 1 0000<Ti​≤1000, 0 ≤ si ≤ 1000≤si≤100, and 0 ≤ a_i < 2\pi0≤ai​<2π. All real numbers in the input have at most 66 digits after the decimal point.

Output

On a single line output the maximum distance the spacecraft can travel. Your answer is considered correct if it has anabsolute or relative error of at most 10^{−6}10−6.

本题答案不唯一，符合要求的答案均正确

样例输入1复制

2
100 1 1
100 1 1.5

样例输出1复制

199.500000

样例输入2复制

4
100 1 0.5
200 1 1
100 0.5 1.5
10 2 3

样例输出2复制

405.500000

#include <iostream>
#include <vector>
#include <algorithm>
#define _USE_MATH_DEFINES
#include <math.h>

#define f first
#define s second

using namespace std;

typedef long long ll;
typedef pair<double, ll> di;
typedef vector<di> vdi;
typedef vector<double> vd;
typedef pair<double, double> dd;
typedef vector<dd> vdd;

int main() {
    ll N;
    cin >> N;
    vd T(N), s(N);
    vd a(N);
    for (ll i = 0; i < N; ++i) {
        cin >> T[i] >> s[i] >> a[i];
    }

    vdd dist_deriv;
    double cur = 0;
    for (ll i = 0; i < N; ++i) {
        if (s[i] != 0 && T[i]/s[i] < M_PI) {
            dist_deriv.emplace_back(a[i] - T[i]/s[i], s[i]);
            dist_deriv.emplace_back(a[i], -s[i]*2);
            dist_deriv.emplace_back(a[i] + T[i]/s[i], s[i]);

            dist_deriv.emplace_back(a[i] - T[i]/s[i] + 2*M_PI, s[i]);
            dist_deriv.emplace_back(a[i] + 2*M_PI, -s[i]*2);
            dist_deriv.emplace_back(a[i] + T[i]/s[i] + 2*M_PI, s[i]);
        } else {
            cur += T[i] - s[i]*M_PI;
            dist_deriv.emplace_back(a[i] - M_PI, s[i]);
            dist_deriv.emplace_back(a[i], -s[i]*2);
            dist_deriv.emplace_back(a[i] + M_PI, 2*s[i]);
            dist_deriv.emplace_back(a[i] + 2*M_PI, -s[i]*2);
            dist_deriv.emplace_back(a[i] + 3*M_PI, s[i]);
        }
    }

    sort(dist_deriv.begin(), dist_deriv.end());

    double last_angle = dist_deriv[0].f;
    double best = cur;
    double c_deriv = 0;

    for (ll i = 0; i < dist_deriv.size(); ++i) {
        cur += c_deriv * (dist_deriv[i].f - last_angle);
        c_deriv += dist_deriv[i].s;
        last_angle = dist_deriv[i].f;
        best = max(best, cur);
    }

    printf("%.6lf\n", best);
}

K. Computer Cache

Your computer has a cache consisting of nn different addresses, indexed from 11 to nn. Each address can contain a singlebyte. The i^{th}ith byte is denoted as a_iai​. Initially all cache bytes start off with the value zero. Formally, the cache can bemodeled by a byte array of length nn that is initially all zeros.

You have mm different pieces of data you want to store. The i^{th}ith piece of data is a byte array x_ixi​ of length s_isi​.You are going to do qq different operations on your computer. There are three types of operations:

11 ii pp

Load data ii starting at position pp in the cache. Formally, this means set a_p = x_{i,1}, a_{p+1} = x_{i,2},...,a_{p+s_i-1} =x_{i,s_i}ap​=xi,1​,ap+1​=xi,2​,...,ap+si​−1​=xi,si​​, where x_{i,k}xi,k​ represents the kkth byte of the array x_ixi​. This overwrites any previously stored value in thecache. It is guaranteed that this is a valid operation (e.g. s_i + p - 1 ≤ nsi​+p−1≤n). It is possible for multiple versions of some data to be loaded in multiple positions at once.

22 pp

Print the byte that is stored in address pp.

33 ii ll rr

Increment the l^{th}lth through r^{th}rth bytes in the i^{th}ith piece of data, modulo 256. Formally, this means to set x_{i,k} =(x_{i,k} + 1)xi,k​=(xi,k​+1) mod 256256 for l ≤ k ≤ rl≤k≤r. This does not affect values that are already loaded in the cache and only affects future loads.

Input

The first line of input consists of three numbers nn, mm, and qq.The following mm lines consist of descriptions of the data, one per line. The following qq lines consist of descriptions of operations, one per line.It is guaranteed there is at least one type 22 print query operation in the input. Additionally:1\le n,m,q \le 5*10^51≤n,m,q≤5∗105, \Sigma_i s_i \le 5*10^5Σi​si​≤5∗105,s_i \ge 1si​≥1,0 \le x_{i,j} \le 2550≤xi,j​≤255

Output

Your program must output the results for each type 2 operation, one integer value per line.

样例输入复制

5 2 10
3 255 0 15
4 1 2 1 3
2 1
1 2 2
1 1 1
2 1
2 4
3 1 1 2
2 1
1 1 2
2 2
2 5

样例输出复制

0
255
1
255
0
3

样例解释

2 1 Nothing has been put into the cache, so print 0

1 2 2 The cache is now [0, 1, 2, 1, 3]

1 1 1 The cache is now [255, 0, 15, 1, 3]

2 1 Print the first value of the cache which is 255

2 4 Print the fourth value of the cache which is 1

3 1 1 2 The first piece of data becomes [0, 1, 15]. The cache is still [255, 0, 15, 1, 3]

2 1 Print the first value of the cache which is 255.

1 1 2 The cache becomes [255, 0, 1, 15, 3].

2 2 Print the second value of the cache which is 0.

2 5 Print the fifth value of the cache which is 3.

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std ;
struct quad {
   int cmd, i, p, r ;
} ;
template<typename T> struct BIT {
   BIT<T>(int n=0) { resize(n) ; }
   void resize(int n) {
      sz = n ;
      arr.resize(4*n+1) ;
   }
   void dorange(int a, int b, int v) {
      while (a < b) {
         int lowb = a & -a ;
         if (lowb == 0) {
            lowb = b + b ;
            while (lowb & (lowb - 1))
               lowb &= lowb-1 ;
         }
         while (a + lowb > b)
            lowb >>= 1 ;
         arr[2*a+lowb].update(v) ;
         a += lowb ;
      }
   }
   int accum(int a) {
      int r = T::zero ;
      for (int b=1; b<2*sz; b *= 2) {
         r = T::sum(r, arr[2*a+b]) ;
         a &= ~b ;
      }
      return r ;
   }
   int sz ;
   vector<T> arr ;
} ;
struct bitsum {
   bitsum() : d(zero) {}
   void update(int v) { d += v ; }
   static int sum(int a, const bitsum &b) { return a+b.d ; }
   static const int zero = 0 ;
   int d ;
} ;
struct bitmax {
   bitmax() : d(zero) {}
   void update(int v) { d = v ; }
   static int sum(int a, const bitmax &b) { return max(a, b.d) ; }
   static const int zero = -1 ;
   int d ;
} ;
int main() {
   int n, m, q ;
   cin >> n >> m >> q ;
   vector<vector<int> > dat(m) ;
   BIT<bitmax> bm(n) ;
   vector<BIT<bitsum> > bsv(m) ;
   for (int i=0; i<m; i++) {
      int ts ;
      cin >> ts ;
      bsv[i].resize(ts) ;
      auto &v = dat[i] ;
      v.resize(ts) ;
      for (auto &u : v)
         cin >> u ;
   }
   vector<quad> cmds(q) ;
   vector<pair<int,int> > setvals ;
   for (int i=0; i<(int)cmds.size(); i++) {
      auto &v = cmds[i] ;
      cin >> v.cmd ;
      switch (v.cmd) {
case 1: cin >> v.i >> v.p ; v.i-- ; v.p-- ;
        bm.dorange(v.p, v.p+dat[v.i].size(), i) ;
        break ;
case 2: cin >> v.p ; v.p-- ;
        {
           int ci = bm.accum(v.p) ;
           if (ci < 0) {
              v.r = 0 ;
           } else {
              v.i = cmds[ci].i ;
              v.p -= cmds[ci].p ;
              setvals.push_back({ci, i}) ;
           }
        }
        break ;
case 3: cin >> v.i >> v.p >> v.r ; v.i-- ; v.p-- ; v.r-- ;
        break ;
      }
   }
   sort(setvals.begin(), setvals.end()) ;
   int svat = 0 ;
   for (int i=0; i<(int)cmds.size(); i++) {
      while (svat < (int)setvals.size() && setvals[svat].first == i) {
         int ci = setvals[svat++].second ;
         int di = cmds[i].i ;
         int add = cmds[ci].p ;
         cmds[ci].r = (bsv[di].accum(add) + dat[di][add]) % 256 ;
      }
      auto &v = cmds[i] ;
      if (v.cmd == 3)
         bsv[v.i].dorange(v.p, v.r+1, 1) ;
   }
   for (int i=0; i<(int)cmds.size(); i++)
      if (cmds[i].cmd == 2)
         cout << cmds[i].r << endl ;
}

L. Carry Cam Failure

“Drat!” cursed Charles. “This stupid carry bar is not working in my Engine! I just tried to calculate the square of anumber, but it’s wrong; all of the carries are lost.”

“Hmm,” mused Ada, “arithmetic without carries! I wonder if I can figure out what your original input was, based onthe result I see on the Engine.”

CarrylessCarryless additionaddition, denoted by \oplus⊕, is the same as normal addition, except any carries are ignored (in base 1010). Thus,37 \oplus 4837⊕48 is 7575, not 8585.

CarrylessCarryless multiplicationmultiplication, denoted by \otimes⊗, is performed using the schoolboy algorithm for multiplication, column bycolumn, but the intermediate additions are calculated using carrylesscarryless additionaddition. More formally, Let a_ma_{m-1}...a_1a_0am​am−1​...a1​a0​be the digits of aa, where a_0a0​ is its least significant digit. Similarly define b_nb_{n-1}...b_{1}b_0bn​bn−1​...b1​b0​ be the digits of bb. The digitsof c = a \otimes bc=a⊗b are given by the following equation:

c_k=a_0b_k \oplus a_1b_{k-1}\oplus ... \oplus a_{k-1}b_1 \oplus a_kb_0,ck​=a0​bk​⊕a1​bk−1​⊕...⊕ak−1​b1​⊕ak​b0​,

where any a_iai​ or b_jbj​ is considered zero if i > mi>m or j > nj>n. For example, 9 \otimes 1 2349⊗1234 is 9 8769876, 90 \otimes 1 23490⊗1234 is 98 76098760, and 99 \otimes 1 23499⊗1234 is 97 53697536.Given NN, find the smallest positive integer a such that a \otimes a = Na⊗a=N.

Input

The input consists of a single line with an integer NN, with at most 2525 digits and no leading zeros.

Output

Print, on a single line, the least positive number aa such that a \otimes a = Na⊗a=N. If there is no such a, print ‘-1−1’ instead.

样例输入1复制

6

样例输出1复制

4

样例输入2复制

123476544

样例输出2复制

11112

样例输入3复制

15

样例输出3复制

-1

#include <iostream>
#include <string>
using namespace std ;
string s, t, r ;
int sqr(int at) {
   int sum = 0 ;
   for (int i=max(0, at-(int)r.size()); i <= at && i<(int)r.size(); i++)
      sum += r[i] * r[at-i] ;
   return s[at] == sum % 10 ;
}
int dfs(int at) {
   if (at >= (int)r.size()) {
      for (; at < (int)s.size(); at++)
         if (!sqr(at))
            return 0 ;
      return 1 ;
   }
   for (int d=0; d<10; d++) {
      r[at] = d ;
      if (!sqr(at))
         continue ;
      int t = dfs(at+1) ;
      if (t)
         return 1 ;
   }
   return 0 ;
}
int main() {
   cin >> s ;
   if (s.size() & 1) {
      t.resize(s.size()) ;
      for (auto &v : s)
         v -= '0' ;
      int rsz = (1+s.size()) >> 1 ;
      r.resize(rsz) ;
      if (dfs(0)) {
         for (auto &v : r)
            v += '0' ;
         cout << r << endl ;
         exit(0) ;
      }
   }
   cout << "-1" << endl ;
}

M. Maze Connect

Given an orthogonal maze rotated 4545 degrees and drawn with forward and backward slash characters (see below),determine the minimum number of walls that need to be removed to ensure it is possible to escape outside of the mazefrom every square of the (possibly disconnected) maze.

/\

\/

This maze has only a single square fully enclosed. Removing any wall will connect it to the outside.

/\..

\.\.

.\/\

..\/

This maze has two enclosed areas. Two walls need to be removed to connect all squares to the outside.

Input

The first line has two numbers, RR and CC, giving the number of rows and columns in the maze's input description.Following this will be RR lines each with CC characters, consisting only of the characters ‘/’, ‘\’, and ‘..’. Both RR and CC are in the range 1...1 0001...1000.Define an odd (even) square as one where the sum of the xx and yy coordinates is odd (even). Either all forward slasheswill be in the odd squares and all backslashes in the even squares, or vice versa.

Output

Output on a single line an integer indicating how many walls need to be removed so escape is possible from everysquare in the maze.

样例输入1复制

2 2
/\
\/

样例输出1复制

1

样例输入2复制

4 4
/\..
\.\.
.\/\
..\/

样例输出2复制

2

样例输入3复制

8 20
/\/\/\/\/\/\/\/\/\/\
\../\.\/./././\/\/\/
/./\.././\/\.\/\/\/\
\/\/\.\/\/./\/..\../
/\/./\/\/./..\/\/..\
\.\.././\.\/\/./\.\/
/.../\../..\/./.../\
\/\/\/\/\/\/\/\/\/\/

样例输出3复制

26

#include <algorithm>
#include <bitset>
#include <cassert>
#include <chrono>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <map>
#include <queue>
#include <random>
#include <set>
#include <stack>
#include <vector>

using namespace std;

const int MAX_SIZE = 1000;
char g[2*MAX_SIZE+2][2*MAX_SIZE+2];
int par[5 * MAX_SIZE * MAX_SIZE];
int find(int x) {
  return par[x] == x ? x : (par[x] = find(par[x]));
}
bool merge(int x, int y) {
  x = find(x);
  y = find(y);
  if(x == y) return false;
  par[x] = y;
  return true;
}
int r, c;
void solve() {
  cin >> r >> c;
  memset(g, '.', sizeof(g));
  for(int i = 0; i < r; i++) {
    string s;
    cin >> s;
    for(int j = 0; j < c; j++) {
      if(s[j] == '.') continue;
      if(s[j] == '/') {
        g[2*i+1][2*j+2] = '#';
        g[2*i+2][2*j+1] = '#';
      }
      else {
        g[2*i+1][2*j+1] = '#';
        g[2*i+2][2*j+2] = '#';
      }
    }
  }
  int maxR = 2 * r + 2;
  int maxC = 2 * c + 2;
  int comps = 0;
  for(int i = 0; i < maxR; i++) {
    for(int j = 0; j < maxC; j++) {
      if(g[i][j] == '#') continue;
      comps++;
      par[i*maxC+j] = i*maxC+j;
      if(i > 0 && g[i-1][j] == '.' && merge((i-1)*maxC + j, i*maxC + j)) comps--;
      if(j > 0 && g[i][j-1] == '.' && merge(i*maxC + j - 1, i*maxC + j)) comps--;
    }
  }
  cout << comps-1 << "\n";
}

int main() {
  solve();
}