Coursera Deep Learning笔记 改善深层神经网络：优化算法

笔记：Andrew Ng's Deeping Learning视频

摘抄：https://xienaoban.github.io/posts/58457.html

本章介绍了优化算法，让神经网络运行的更快

1. 梯度优化算法

1.1 Mini-batch 梯度下降

将 \(X = [x^{(1)}, x^{(2)}, x^{(3)}, ..., x^{(m)}]\) 矩阵所有 \(m\) 个样本划分为 \(t\) 个子训练集,每个子训练集，也叫做mini-batch；

每个子训练集称为 \(x^{\{i\}}\), 每个子训练集内样本个数均相同(若每个子训练集有1000个样本, 则 \(x^{\{1\}} = [x^{(1)}, x^{(2)}, ..., x^{(1000)}]\)，维度为 \((n_x,1000)\).

例：把\(x^{(1)}\)到\(x^{(1000)}\) 称为 \(X^{\{1\}}\), 把\(x^{(1001)}\)到\(x^{(2000)}\) 称为 \(X^{\{2\}}\)，如果你的训练样本一共有500万个，每个mini-batch都有1000个样本，也就是说，你有5000个mini-batch, 因为5000*1000=500万， 最后得到的是 \(X^{\{5000\}}\) 】

若m不能被子训练集样本数整除, 则最后一个子训练集样本可以小于其他子训练集样本数。 \(Y\) 亦然.

训练时, 每次迭代仅对一个子训练集（mini-batch）进行梯度下降:

\(On \ iteration \ t:\)

\[\begin{aligned}
& \text{Repeat} :\\
& \qquad \text{For } i = 1, 2, ..., t: \\
& \qquad \qquad \text{Forward Prop On } X^{\{i\}} \\
& \qquad \qquad \text{Compute Cost } J^{\{i\}} \\
& \qquad \qquad \text{Back Prop using } X^{\{i\}}, Y^{\{i\}}\\
& \qquad \qquad \text{Update } w, b
\end{aligned}
\]

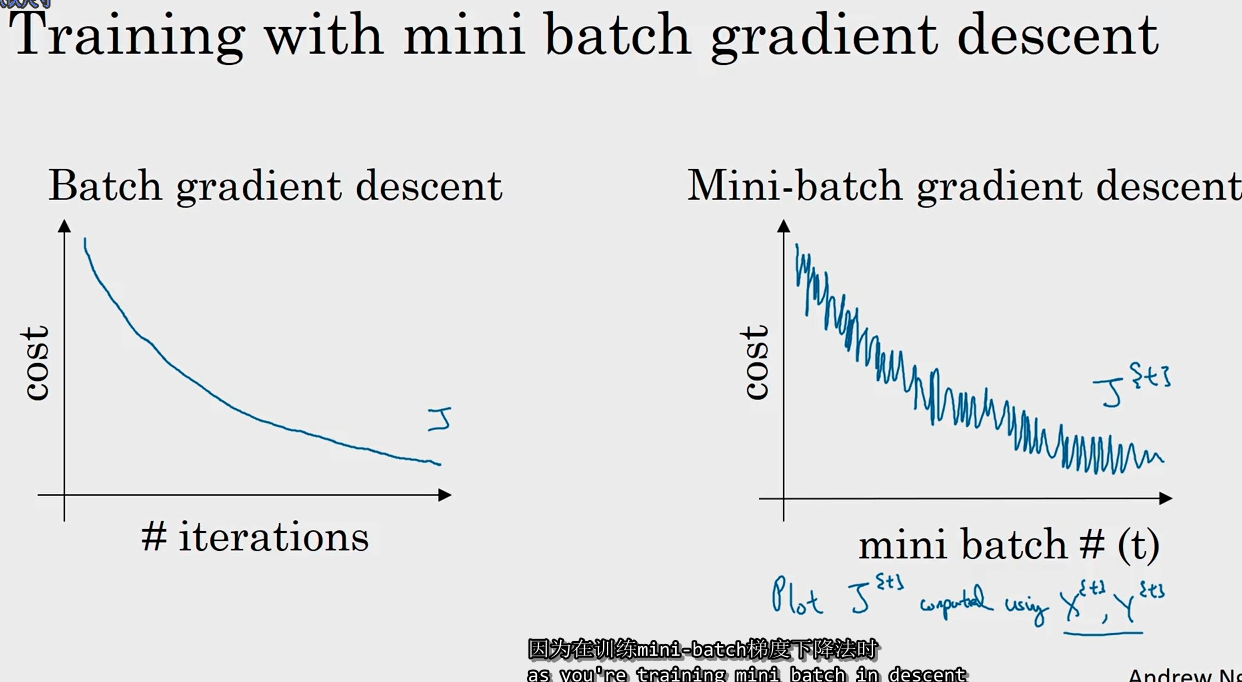
• 使用 batch 梯度下降法时：

  • 一次遍历训练集只能让你做一个梯度下降；每次迭代都遍历整个训练集

  • 预期每次迭代成本都会下降

• 但若使用 mini-batch 梯度下降法

  • 一次遍历训练集，能让你做5000个梯度下降；如果想多次遍历训练集，你还需要另外设置一个while循环...

  • 若对成本函数作图, 并不是每次迭代都下降, 噪声较大, 但整体上走势还是朝下的.

• 若样本集较小(小于2000), 无需使用 mini-batch;
• 否则一般的 mini-batch 大小为 64~512, 通常为 2 的整数次方.

1.2 指数加权平均数(Exponentially Weighted Averages)

这个不是优化算法，是下面的优化方法的数学基础.

\(v_t = \beta v_{t-1} + (1 - \beta)\theta_t, \qquad \beta \in[0,1)\)

\(\beta\) 越大, 画得曲线越 平滑, 但画得图像会更为偏右.

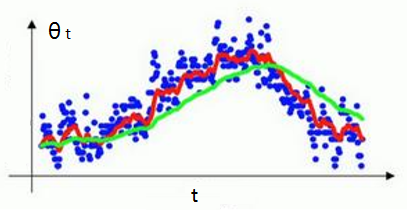
为了让加权平均数运算更准确（为了在早期获得更好的评估）, 我们还需要偏差修正(Bias Correction).

由于我们默认\(v_0 = 0\), 因此当t较小时, \(v_t\) 会比 \(θ_t\) 小很多.

• 为解决这一问题, 得到更准确的估测, 我们不使用 \(v_t\), 而使用 \(\frac{v_t}{1-\beta^t}\).
  
  

1.3 动量梯度下降法(Gradient Descent With Momentum)

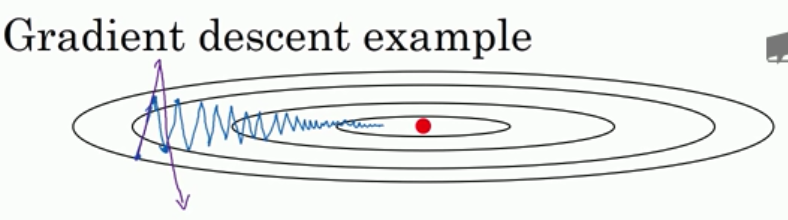
当你的成本函数图像不够圆润, 例如是个很扁的椭圆, 使得梯度下降 在y轴很快而在x轴很慢.

• 此时增加学习率会偏离函数的范围(摆动过大), 减小就更慢了。

动量梯度下降法(Momentum) 使用指数加权平均数(计算梯度的指数加权平均数,并用该梯度更新你的权重):

\(On \ iteration \ t:\)

\[\begin{aligned}
v_{dW} & = \beta v_{dW} + (1 - \beta)dW \\
v_{db} & = \beta v_{db} + (1 - \beta)db \\
W & = W - \alpha v_{dW} \\
b & = b - \alpha v_{db}
\end{aligned}
\]

竖轴平均值相互抵消，横轴轴平均值仍然很大，以此减缓梯度下降摆动幅度.

1.4 RMSprop(Root Mean Square prop)

全称是均方根，同 Momentum, 能够很好的消除摆动，减缓竖轴方向的学习，加快横轴方向的学习

\(On \ iteration \ t:\)

\[\begin{aligned}
S_{dW} & = \beta S_{dW} + (1 - \beta)(dW)^2 \\
S_{db} & = \beta S_{db} + (1 - \beta)(db)^2 \\
W & = W - \alpha \frac{dW}{\sqrt{S_{dW}}} \\
b & = b - \alpha \frac{db}{\sqrt{S_{db}}}
\end{aligned}
\]

例如：

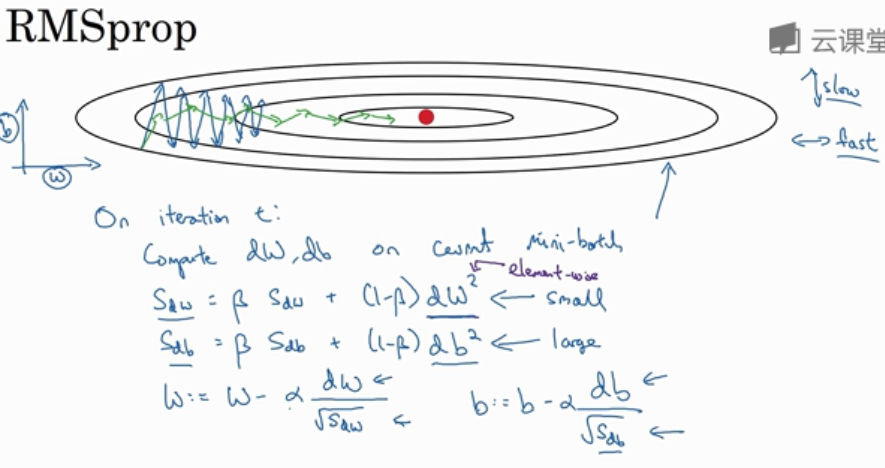
• 允许你使用一个更大的学习率 \(\alpha\) 加快学习速度

• db的平方较大，\(s_{db}\) 也会较大，相比之下 dw会小一些，\(s_{dw}\)会较小；

• 结果就是纵轴上的数(b)要被一个较大的数相除，就能消除摆动，水平方向被较小的数相除。

1.5 Adam 优化算法(Adaptive Moment Estimation)

RMSprop 与 Adam 是少有的经受住人们考验的两种算法.

Adam 的本质就是将 Momentum 和 RMSprop 结合在一起. 使用该算法首先需要初始化:

\[v_{dW} = 0, S_{dW} = 0, v_{db} = 0, S_{db} = 0.
\]

在第t次迭代中,梯度下降后:

\[\begin{aligned}
v_{dW} & = \beta_1 v_{dW} + (1 - \beta_1)dW \\
v_{db} & = \beta_1 v_{db} + (1 - \beta_1)db \\
S_{dW} & = \beta_2 S_{dW} + (1 - \beta_2)(dW)^2 \\
S_{db} & = \beta_2 S_{db} + (1 - \beta_2)(db)^2 \\
v_{dW}^{\text{corrected}} & = \frac{v_{dW}}{1-\beta_1^t}, \quad
v_{db}^{\text{corrected}} = \frac{v_{db}}{1-\beta_1^t} \\
S_{dW}^{\text{corrected}} & = \frac{S_{dW}}{1-\beta_2^t}, \quad
S_{db}^{\text{corrected}} = \frac{S_{db}}{1-\beta_2^t} \\
W & = W - \alpha\frac{v_{dW}^{\text{corrected}}}{\sqrt{S_{dW}^{\text{corrected}}+\varepsilon}} \\
b & = b - \alpha\frac{v_{db}^{\text{corrected}}}{\sqrt{S_{db}^{\text{corrected}}+\varepsilon}}
\end{aligned}
\]

最后两个式子的 \(+ \varepsilon\) 是为了防止分母为0, 上面 RMSprop 的分母实践中一般也加上, \(\varepsilon\) 通常取 \(10^{-8}\).

超参数选择：

超参数	值
\(\alpha\)	need to be tuned
\(\beta_1\)	0.9 (dw)
\(\beta_2\)	0.999 (dw^2)
\(\varepsilon\)	\(10^{-8}\)

Adam 算法结合了 Momentum 和 RMSprop 梯度下降法, 并且是一种极其常用的学习算法, 被证明能有效适用于不同神经网络. 适用于广泛的结构.

2. 超参数调整优化

2.1 学习率衰减(Learning Rate Decay)

如果使用固定的学习率 \(\alpha\), 在使用 mini-batch 时在最后的迭代过程中会有噪音, 不会精确收敛, 最终一直在附近摆动. 因此我们希望在训练后期 \(\alpha\) 不断减小.

以下为几个常见的方法:

法一：

\[\alpha = \frac{1}{1+decay\_rate*\text{epoch-num}} \alpha_0
\]

其中 \(\alpha_0\) 为初始学习率; \(epoch-num\) 为当前迭代的代数; \(decay\_rate\) 是衰减率, 一个需要调整的超参数.

法二：

\[\alpha = 0.95^{\text{epoch-num}} \alpha_0
\]

其中 0.95 自然也能是一些其他的小于 1 的数字.

法三：

\[\alpha = \frac{k}{\sqrt{\text{epoch-num}}} \alpha_0
\]

法四:

离散下降(discrete stair cease), 过一阵子学习率减半, 过一会又减半.

法五:

手动衰减, 感觉慢了就调快点, 感觉快了就调慢点.

3. 局部最优问题(Local Optima)

• 人们经常担心算法困在局部最优点, 而事实上算法更经常被困在鞍点, 尤其是在高维空间中

• 成熟的优化算法如 Adam 算法，能够加快速度，让你尽早往下走出平稳段.