Regularizing Deep Networks with Semantic Data Augmentation

目录

• 概
• 主要内容
• 代码

Wang Y., Huang G., Song S., Pan X., Xia Y. and Wu C. Regularizing Deep Networks with Semantic Data Augmentation.

TPAMI.

概

通过data augments来对数据进行扩充, 可以有效提高网络的泛化性.

但是这些transformers通常只有一些旋转, 剪切等较为简单的变换, 想要施加更为复杂的语义不变变换(如切换背景), 可能就需要GAN等引入额外的网络来进行.

本文提出的ISDA算法是基于特征的变化进行的, 技能进行语义层面的变换, 又没有GAN等方法的计算昂贵的缺点.

主要内容

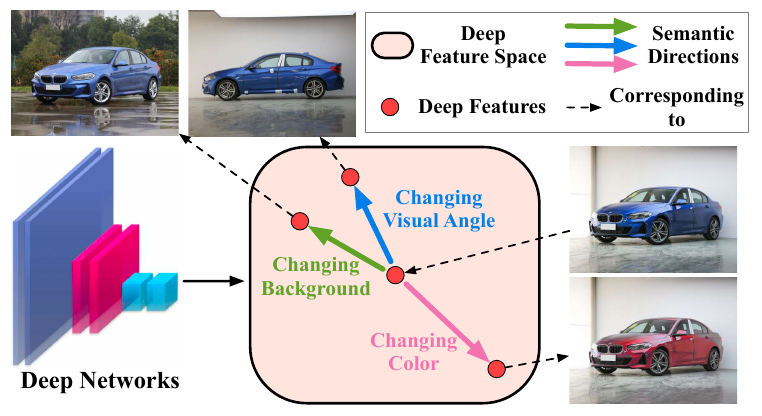
作者认为, 在最后的特征层, 通过增加一定的平移对应不同的语义上的变换.

但是, 作者也指明了, 并非所有的方向都是一个有意义的方向, 比如这个方向可能是戴上眼镜, 这个方向对于人来说是有意义的, 但是对于汽车飞机就没有意义了.

所以我们需要从一个有意义的分布中采样, 作者假设该分布是一个零均值的正态分布, 即

\[\mathcal{N}(0, \Sigma).
\]

于是乎, 现在的问题就是如何选择这个协方差矩阵\(\Sigma\).

就像之前讲的, 有些方向是否有意义与类别有关系, 所以不同的类别的样本会从不同的正态分布

\[\mathcal{N}(0, \Sigma_i),
\]

中采样.

对于每一个协方差矩阵, 作者采用online的更新方式更新:

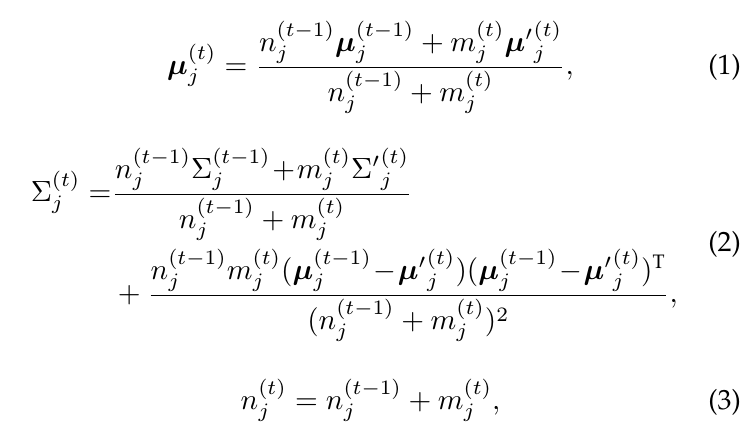
上图是式子就是普通的协方差估计式子

\[\frac{1}{n}\sum_{i=1}^n (x_i-\mu)(x_i - \mu)^T,
\]

的online更新版本.

如果假设样本\(x\)经过encoder之后的特征为\(a\), 则其变换后的版本

\[a' \sim \mathcal{N}(a, \Sigma_y),
\]

其中\(y\)为\(x\)的类别标签. 于是一般的对应的损失函数即为

\[\mathcal{L}_{M}(M, b, \Theta) = \frac{1}{N}\sum_{i=1}^N\frac{1}{M}\sum_{m=1}^M - \log (\frac{e^{w_{y_i}^Ta_i^m+b_{y_i}}}{\sum_{j=1}^Ce^{w_{j}^Ta_i^m+b_{j}}}),
\]

当我们令\(M\)趋于无穷大的时候,

\[\mathcal{L}_{M}(M, b, \Theta) = \frac{1}{N}\sum_{i=1}^N\mathbb{E}_{a_i}- \log (\frac{e^{w_{y_i}^Ta_i+b_{y_i}}}{\sum_{j=1}^Ce^{w_{j}^Ta_i+b_{j}}}).
\]

这个式子没有显示解, 故作者退而求其次, 最小化其上界.

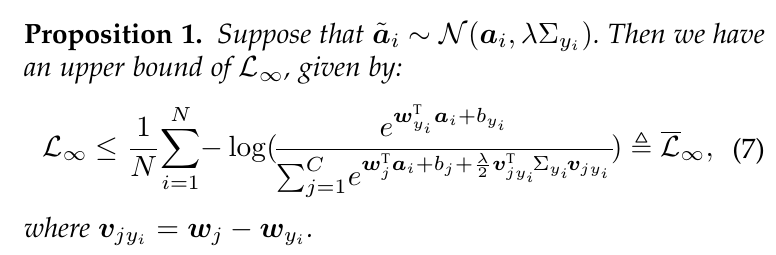
这个证明不难, 这里就练习一下

\[\mathbb{E}[e^{tX}]=e^{t\mu + \frac{1}{2}\sigma^2t^2}, \quad X \sim \mathcal{N}(\mu, \sigma^2).
\]

既然

\[\mathbb{E}[e^{tX}] = e^{\frac{(t\sigma^2+\mu)^2-\mu^2}{2\sigma^2}}.
\]

代码

原文代码