巧妙地用二叉树完成算式计算算法<计算器，二叉树，C++，独辟蹊径>

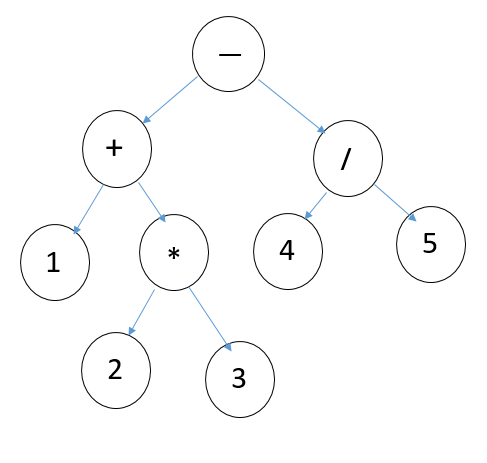
#01、引言，我们知道算式计算的问题是栈里面一个非常经典的题目。但是用栈来实现是一个非常麻烦的过程，第一要解决算式判断，是否为符合规则的算式，第二要由中最表达式转化为后缀表达式。这两个部分是栈实现计算算式表达式的比较复杂的地方。不仅如此，栈实现里面的各种运算符的优先级，各种条件判断，可以说是麻烦的要命。但是，实际上有一种数据结构比栈更适合解决这类问题。可以说是得天独厚的优势。对，就是二叉树。例如一个表达式：1+2*3-4/5

我们构造这样一个二叉树

当构造这样一个二叉树之后，解决表达式的值的方法，也就浮出水面了，把2和3相乘，存到*的节点中，然后再和1相加，存到+的节点中.....最后根节点-节点中存放的就是最后的计算结果。就是叶子节点执行其双亲节点的运算，结果存到双亲节点中。

#02、选二叉树作为算法的存储结构有什么好处。

       这主要有两个方面的好处，这也是针对于栈算法的两个麻烦的地方。

<1>//免除了算式表达式的检查过程。为什么能免除检查，表达式的规范性呢？并不是不需要检查，而是检查的过程就包含在创建二叉树的过程。认真分析这棵二叉树，我们会发现，所有的叶子节点必须是操作数节点，而所有的非叶子节点必须是运算符节点，否则表达式的结构一点不正确，创建二叉树的过程就可以对表达式经行检查。表达式是否正确也只取决于两个方面，第一、表达式的结构是否正确，比如不能出现2*+6这样的表达式，第二、表达式的数据是否正确，例如不能出现1+2.2.3这样的表达式，2.2.3不是一个符合规则的数据。而数据的检查，也可以在给叶子节点赋值的时候检查。所以避免的单独经行表达式检查的繁琐。

<2>//不需要转化为后缀表达式再经行表达式结果的计算，这也是得益于二叉树这种结构的天然优势，自我感觉就完全是为这种算法题设计的，天造地设嘛！

#03、算法实现

       0x001、数据结构的定义：

 #define Maxsize 100
 //定义数据元素类型
 typedef char  elemtype;
 //定义二叉树数据变量
 typedef union
 {
     char Operator;
     double date;
 }perdate;
 //定义二叉树链式存储结构
 typedef struct node
 {
     perdate DATE;//用union类型存运算符或操作数
     struct node *lchild;
     struct node *rchild;
 }btnode;　　　　

 struct op
 {
     char opration;
     int index;//括号层数//当这个index被标记为-1时，就不会再次被查找到
     int locate;//op的位置
 };

用union定义一个perdate类型，用来分别记录操作数和运算符。op是查找运算符时用，从后往前查找，括号级数最低的作为根节点来创建二叉树。

0x002、实现的函数

//查找op，并填充Aop数组
int Sortop(char str[], op Aop[], int &index);
//将字符串转化为浮点数
double str_to_flaot(char strpoly[], int p,int q);
//判断数组是不是1.2类型，就是只有数据
bool isdate(char str[],int p,int q);//p,q指向str的开始和结尾处
//判断str是否为运算符和括号
bool isoprater(char str[],int p,int q);//p,q指向str的开始和结尾处
//用算数表达式创建二叉树
void Createbtnode(btnode *b, char *str, int p, int q,int tail);//p,q指向str的开始和结尾处；tail是Aop的尾指针
//计算二叉树算式的结果
double Comp(btnode *b);

0x003、main函数，整个算法过程简述

#include"标头.h"
int index = ;//记录最大的括号层数
struct op Aop[Maxsize];

 int main()
 {
     btnode * b;
     b = new btnode;
     char str[Maxsize];
     cout << "算式计算器[张安源]" << endl;
         while(true)
         {
             cout << "[Type \"exit\" to exit]" << endl << "请输入你要求的表达式：" << endl;
            cin.getline(str, Maxsize);
           if (strcmp("exit", str) == )  break;//如果输入的是exit则退出
           else
           {
               int tail = Sortop(str, Aop, index);//整理得到Aop的结构数组
               Createbtnode(b, str, , strlen(str) - , tail);
               double result = Comp(b);
               cout << result << endl;
           }
         }
 }

一直循环，让用户输入一个表达式，当输入为exit时，退出循环。Sortop函数将表达式的操作符的括号层数和其在表达式的位置经行记录到Aop数组里面，返回值是最大的括号层数。然后由Createbtnode函数创建一个二叉树b。comp求出二叉树表达式的结构，然后输出结果。大致的过程是这样，但是里面却还包含了一些实现的细节，具体代码是怎么实现的就不啰嗦了，看代码比讲解跟方便。

0x004、整个project。

<1>Header.h

 #pragma once
 #include<iostream>
 using namespace std;
 #define Maxsize 100
 //定义数据元素类型
 //*********int check = 0;//作为判断表达式是否正确的标记
 typedef char  elemtype;
 //定义二叉树数据变量
 typedef union
 {
     char Operator;
     double date;
 }perdate;
 //定义二叉树链式存储结构
 typedef struct node
 {
     perdate DATE;//用union类型存运算符或操作数
     struct node *lchild;
     struct node *rchild;
 }btnode;
 //定义查找运算符的结构数组
 struct op
 {
     char opration;
     int index;//括号层数//当这个index被标记为-1时，就不会再次被查找到
     int locate;//op的位置
 };
 extern int index;
 extern struct op Aop[Maxsize];
 //******************************************************
 //查找op，并填充Aop数组
 int Sortop(char str[], op Aop[], int &index);
 //将字符串转化为浮点数
 double str_to_flaot(char strpoly[], int p,int q);
 //判断数组是不是1.2类型，就是只有数据
 bool isdate(char str[],int p,int q);//p,q指向str的开始和结尾处
 //判断str是否为运算符和括号
 bool isoprater(char str[],int p,int q);//p,q指向str的开始和结尾处
 //用算数表达式创建二叉树
 void Createbtnode(btnode *b, char *str, int p, int q,int tail);//p,q指向str的开始和结尾处；tail是Aop的尾指针
 //计算二叉树算式的结果
 double Comp(btnode *b);

<2>op.cpp

 #include"标头.h"
 //查找op，并填充Aop数组
 int Sortop(char str[], op Aop[], int &index)
 {
     int j = ;//记录Aop的top
     int i;
     int ind = ;//记录括号层数
     for (i = ; str[i] != '\0'; i++)
     {
         if (str[i] == '(')
             ind++;
         else if (str[i] == ')')
             ind--;
         else if (str[i] == '+' || str[i] == '-' || str[i] == '*'||str[i]=='/' || str[i] == '^')
         {
             Aop[j].opration = str[i];
             Aop[j].index = ind;
             Aop[j].locate = i;
             j++;
         }
         index = (index > ind) ? index : ind;
     }
     return j;
 }
 //将字符串转化为浮点数
 double str_to_flaot(char strpoly[], int p,int q)
 {
     if (strpoly[p] == '(')
         p++;
     if (strpoly[q] == ')')
         q--;
     //判断小数点前有几位数字
     int index = ;
     int temp = p;//保存原来的p值
     double  n = ;//最后的浮点数
     for (;( p <= q)&&(strpoly[p]!='.'); p++) index++;
     p = temp;
     for (; p<=q; p++)
     {
         if (strpoly[p] == '.')  continue;
         index--;
         n = n + ((double)(strpoly[p] - ''))*(pow(, index));

     }
         return n;
 }
 //判断数组是不是1.2类型，就是只有数据//忽略括号
 bool isdate(char str[],int p,int q)
 {
     int i;
     int index = ;
     for (i = p; i<=q; i++)
     {
         if (str[i] == '.')
             index++;
         if (str[i] == '+' || str[i] == '-' || str[i] == '*' ||str[i]=='/' || str[i] == '^')
             return false;
     }
     if (index==  || index == )
     {
         return true;
     }
     else
         abort();
 }
 //判断str是否为运算符和括号
 bool isoprater(char str[],int p,int q)
 {
     if ((p==q)&&(str[p] == '(' || str[p] == ')' || str[p] == '*'||str[p]=='/' || str[p] == '^' || str[p] == '+' || str[p] == '-'))
         return true;
     else
         return false;
 }
 //用算数表达式创建二叉树
 void Createbtnode(btnode *b, char *str, int p, int q,int tail)        //由str串创建二叉链
 {                                                            //p,q分别标志Aop的首尾
     int i = ;
     int j = ;//
     int find=;
     if (isdate(str,p,q))//str为1.3类型
     {
         //创建头节点，并将数据位置为str_to_double
         b->DATE.date = str_to_flaot(str,p,q);
         b->lchild = NULL;
         b->rchild = NULL;
     }
     else if (isoprater(str,p,q))//str为+、—、^、（、）、*
     {
         abort();
         b->DATE.Operator = str[i];
         b->lchild = NULL;
         b->rchild = NULL;
     }
     ///***************************************************************
     else
         for (int temp = ; temp <= index; temp++)
         {
             for (j = tail; j >=; j--)//从后往前找，才符合运算的法则，前面先算后面后算
             {
                 if (Aop[j].index == temp && ((Aop[j].opration == '+')||(Aop[j].opration == '-')) && Aop[j].locate >= p&&Aop[j].locate <= q)
                 {
                     find++;
                     Aop[j].index = -;//标志这个已经被找过了
                     btnode *lt, *rt;
                     lt = new btnode;
                     rt = new btnode;
                     b->lchild = lt;
                     b->rchild = rt;
                     b->DATE.Operator = Aop[j].opration;
                     Createbtnode(b->lchild, str, p, Aop[j].locate - ,tail);
                     Createbtnode(b->rchild, str, Aop[j].locate+, q,tail);
                 }
             }
         if(find==)
             for (j = tail; j >=; j--)
             {
                 if (Aop[j].index == temp && ((Aop[j].opration == '*')||(Aop[j].opration=='/')) && Aop[j].locate >= p&&Aop[j].locate <= q)
                 {
                     find++;
                     Aop[j].index = -;//标志这个已经被找过了
                     btnode *lt, *rt;
                     lt = new btnode;
                     rt = new btnode;
                     b->lchild = lt;
                     b->rchild = rt;
                     b->DATE.Operator = Aop[j].opration;
                     Createbtnode(b->lchild, str, p, Aop[j].locate - ,tail);
                     Createbtnode(b->rchild, str, Aop[j].locate+, q,tail);
                 }
             }
         if(find==)
             for (j = tail; j >=; j--)
             {
                 if (Aop[j].index == temp && (Aop[j].opration == '^') && Aop[j].locate >= p&&Aop[j].locate <= q)
                 {
                     Aop[j].index = -;//标志这个已经被找过了
                     btnode *lt, *rt;
                     lt = new btnode;
                     rt = new btnode;
                     b->lchild = lt;
                     b->rchild = rt;
                     b->DATE.Operator = Aop[j].opration;
                     Createbtnode(b->lchild, str, p, Aop[j].locate - ,tail);
                     Createbtnode(b->rchild, str, Aop[j].locate+, q,tail);
                 }
             }
         }
 }
 //计算二叉树算式的结果
 double Comp(btnode *b)
 {
     double v1, v2;
     if (b == NULL) return ;
     if (b->lchild == NULL && b->rchild == NULL)
         return b->DATE.date;    //叶子节点直接返回节点值
     v1 = Comp(b->lchild);
     v2 = Comp(b->rchild);
     switch (b->DATE.Operator)
     {
     case '+':
         return v1 + v2;
     case '-':
         return v1 - v2;
     case '*':
         return v1*v2;
     case '/':
         if (v2 != )
             return v1 / v2;
         else
             abort();
     case '^':
         return (pow(v1, v2));
     default:
         abort();
     }
 }

<3>main.cpp

 #include"标头.h"
 int index = ;//记录最大的括号层数
 struct op Aop[Maxsize];
 int main()
 {
     btnode * b;
     b = new btnode;
     char str[Maxsize];
     cout << "算式计算器[张安源]" << endl;
         while(true)
         {
             cout << "[Type \"exit\" to exit]" << endl << "请输入你要求的表达式：" << endl;
            cin.getline(str, Maxsize);
           if (strcmp("exit", str) == )  break;//如果输入的是exit则退出
           else
           {
               int tail = Sortop(str, Aop, index);//整理得到Aop的结构数组
               Createbtnode(b, str, , strlen(str) - , tail);
               double result = Comp(b);
               cout << result << endl;
           }
         }
 }

#04算法测试

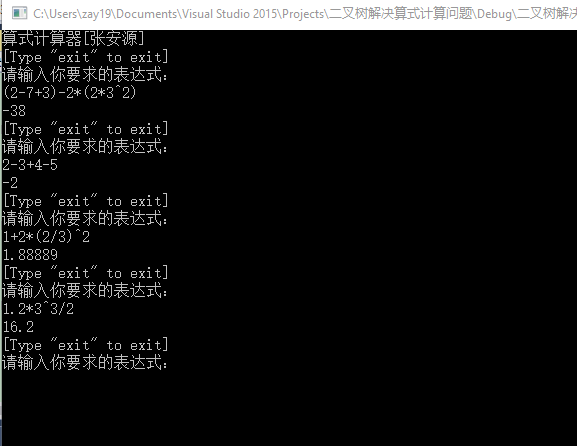
当输入的表达式符合规则时，返回表达式的值。

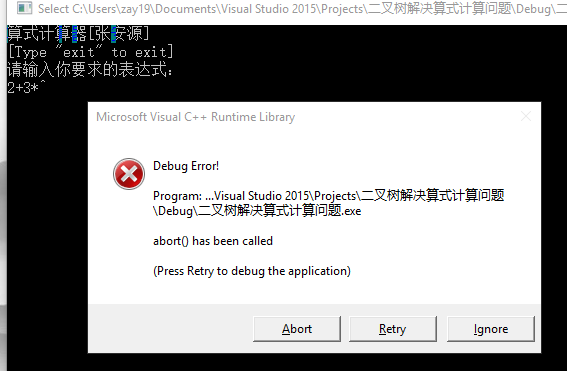
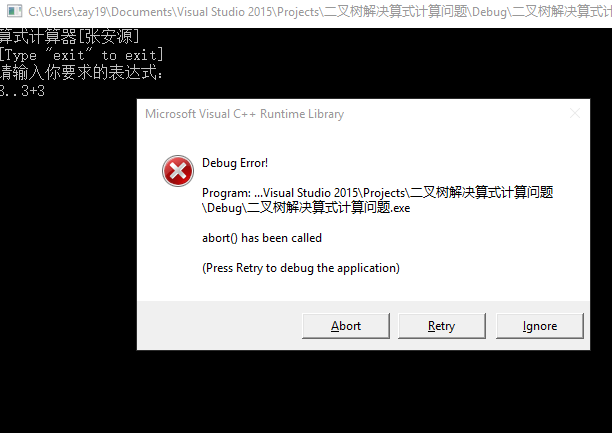
当输入的表达式不符合规则时，则调用abort函数。

#05、总结

好的数据结构能事半功倍，要培养善于发现的思维，当有某个思路然后去实现它，另外要积累经验。好好理解数据结构！