AdaBoost

一直想写Adaboost来着，但迟迟未能动笔。其算法思想虽然简单“听取多人意见，最后综合决策”，但一般书上对其算法的流程描述实在是过于晦涩。昨日11月1日下午，邹博在我组织的机器学习班第8次课上讲决策树与Adaboost，其中，Adaboost讲得酣畅淋漓，讲完后，我知道，可以写本篇博客了。

无心啰嗦，本文结合邹博之决策树与Adaboost的PPT跟《统计学习方法》等参考资料写就，可以定义为一篇课程笔记、读书笔记或学习心得，有何问题或意见，欢迎于本文评论下随时不吝指出，thanks。

1 Adaboost的原理

1.1 Adaboost是什么

AdaBoost，是英文"Adaptive Boosting"（自适应增强）的缩写，由Yoav Freund和Robert Schapire在1995年提出。它的自适应在于：前一个基本分类器分错的样本会得到加强，加权后的全体样本再次被用来训练下一个基本分类器。

AdaBoost是一种迭代算法，在每一轮中加入一个新的弱分类器，直到达到某个预定的足够小的错误率。每一个训练样本都被赋予一个权重，表明它被某个分类器选入训练集的概率。如果某个样本点已经被准确地分类，那么在构造下一个训练集中，它被选中的概率就被降低；相反，如果某个样本点没有被准确地分类，那么它的权重就得到提高。

在具体实现上，最初令每个样本的权重都相等，对于第k次迭代操作，我们就根据这些权重来选取样本点，进而训练分类器。然后就根据这个分类器，来提高被它分错的的样本的权重，并降低被正确分类的样本权重。然后，权重更新过的样本集被用于训练下一个分类器。整个训练过程如此迭代地进行下去。

1.2 Adaboost算法流程

给定一个训练数据集T={(x1,y1), (x2,y2)…(xN,yN)}，其中实例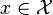，而实例空间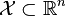，yi属于标记集合{-1,+1}，Adaboost的目的就是从训练数据中学习一系列弱分类器或基本分类器，然后将这些弱分类器组合成一个强分类器。

Adaboost的算法流程如下：

· 1.首先，初始化训练数据的权值分布。每一个训练样本最开始时都被赋予相同的权重：1/N。

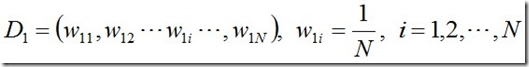
接下来，如果某个样本点已经被准确地分类，那么在构造下一个训练集中，它被选中的概率就被降低；相反，如果某个样本点没有被准确地分类，那么它的权重就得到提高。具体说来，则是：

· 2.对于m = 1,2, ..., M

a.使用具有权值分布Dm的训练数据集学习，得到基本二元分类器：

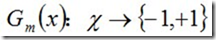
b.计算Gm(x)在训练数据集上的分类误差率

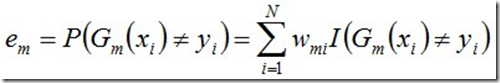
c. 计算Gm(x)的系数，am表示Gm(x)在最终分类器中的重要程度：

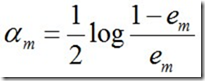
由上述式子可知，em <= 1/2时，am >= 0，且am随着em的减小而增大，意味着分类误差率越小的基本分类器在最终分类器中的作用越大。

d. 更新训练数据集的权值分布

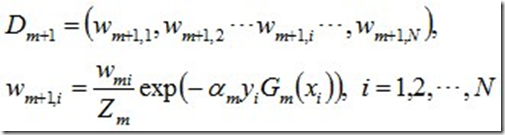
使得被基本分类器Gm(x)误分类样本的权值增大，而被正确分类样本的权值减小。就这样，通过这样的方式，AdaBoost方法能“聚焦于”那些较难分的样本上。

其中，Zm是规范化因子，使得Dm+1成为一个概率分布：

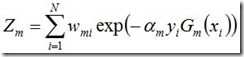
· 3.构建基本分类器的线性组合

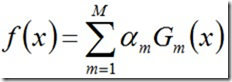
从而得到最终分类器，如下：

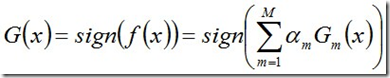
1.3 Adaboost的一个例子

下面，给定下列训练样本，请用AdaBoost算法学习一个强分类器。

求解过程：初始化训练数据的权值分布，令每个权值W1i = 1/N = 0.1，其中，N = 10，i = 1,2, ..., 10，然后分别对于m = 1,2,3, ...等值进行迭代。

--------------------------------------

迭代过程1：对于m=1，在权值分布为D1的训练数据上，阈值v取2.5时误差率最低，故基本分类器为：

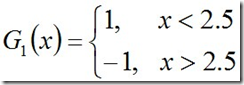
从而可得G1(x)在训练数据集上的误差率e1=P(G1(xi)≠yi) = 0.3 (x=6,7,8时的分类分错，故e1=0.1+0.1+0.1)

然后计算G1的系数：

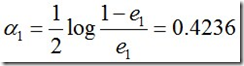
接着更新训练数据的权值分布：

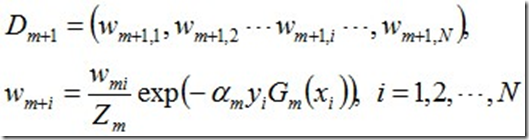
最后得到各个数据的权值分布D2=(0.0715, 0.0715, 0.0715, 0.0715, 0.0715, 0.0715, 0.1666, 0.1666, 0.1666, 0.0715)，分类函数f1(x)=0.4236G1(x)，故最终得到的分类器sign(f1(x))在训练数据集上有3个误分类点。

----------------------------------------------------

迭代过程2：对于m=2，在权值分布为D2的训练数据上，阈值v取8.5时误差率最低，故基本分类器为：

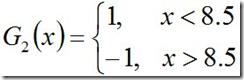
G2(x)在训练数据集上的误差率e2=P(G2(xi)≠yi) = 0.2143

计算G2的系数：

更新训练数据的权值分布：

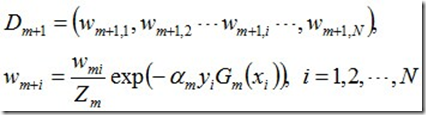
D3=(0.0455, 0.0455, 0.0455, 0.1667, 0.1667, 0.01667, 0.1060, 0.1060, 0.1060, 0.0455)

f2(x)=0.4236G1(x) + 0.6496G2(x)

分类器sign(f2(x))在训练数据集上有3个误分类点。

----------------------------------------------------

迭代过程3：对于m=3，在权值分布为D3的训练数据上，阈值v取5.5时误差率最低，故基本分类器为：

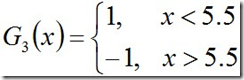
G3(x)在训练数据集上的误差率e3=P(G3(xi)≠yi) = 0.1820

计算G3的系数：

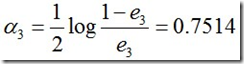
更新训练数据的权值分布：

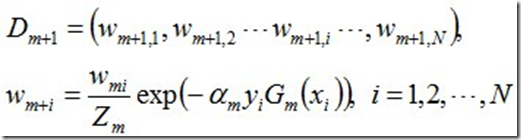
D4=(0.125, 0.125, 0.125, 0.102, 0.102, 0.102, 0.065, 0.065, 0.065, 0.125)，f3(x)=0.4236G1(x) + 0.6496G2(x)+0.7514G3(x)，分类器sign(f3(x))在训练数据集上有0个误分类点。

--------------------------------------------------------

2 Adaboost的误差界

通过上面的例子可知，Adaboost在学习的过程中不断减少训练误差e，那这个误差界到底是多少呢？

事实上，adaboost 的训练误差的上界为：

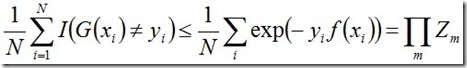
下面，咱们来通过推导来证明下上述式子。

当G(xi)≠yi时，yi*f(xi)<0，因而exp(-yi*f(xi))≥1，因此前半部分得证。

关于后半部分，别忘了：

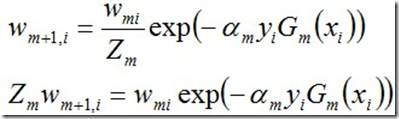
整个的推导过程如下：

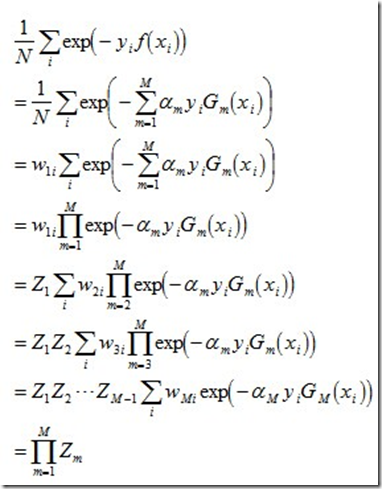
这个结果说明，可以在每一轮选取适当的Gm使得Zm最小，从而使训练误差下降最快。接着，咱们来继续求上述结果的上界。

对于二分类而言，有如下结果：

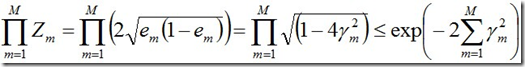
其中，。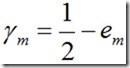

继续证明下这个结论。

由之前Zm的定义式跟本节最开始得到的结论可知：

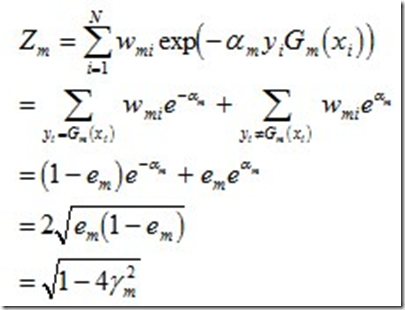
而这个不等式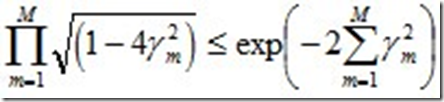可先由e^x和1-x的开根号，在点x的泰勒展开式推出。

值得一提的是，如果取γ1, γ2… 的最大值，记做γ（显然，γ≥γi>0，i=1,2,...m），则对于所有m，有：

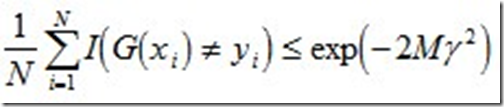
这个结论表明，AdaBoost的训练误差是以指数速率下降的。另外，AdaBoost算法不需要事先知道下界γ，AdaBoost具有自适应性，它能适应弱分类器各自的训练误差率 。

最后，Adaboost 还有另外一种理解，即可以认为其模型是加法模型、损失函数为指数函数、学习算法为前向分步算法的二类分类学习方法，有机会再推导下，然后更新此文。而在此之前，有兴趣的可以参看《统计学习方法》第8.3节或其它相关资料。

3 参考文献与推荐阅读

1. wikipedia上关于Adaboost的介绍：http://zh.wikipedia.org/zh-cn/AdaBoost；

1. 邹博之决策树与Adaboost PPT：http://pan.baidu.com/s/1hqePkdY；

1. 《统计学习方法 李航著》第8章；

1. 关于adaboost的一些浅见：http://blog.sina.com.cn/s/blog_6ae183910101chcg.html；

1. A Short Introduction to Boosting：http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.93.5148&rep=rep1&type=pdf；

1. 南大周志华教授做的关于boosting 25年的报告PPT：http://vdisk.weibo.com/s/FcILTUAi9m111；

1. 《数据挖掘十大算法》第7章 Adaboost。

--------------------------------------------------------------------------------------------------------------------
相应的Python代码如下
--------------------------------------------------------------------------------------------------------------------

# -*- coding: utf-8 -*-
# ---------------------------------------------------------------------------
# AdaBoost.py
# Created on: 2014-06-12 09:49:56.00000
# Description:
# ---------------------------------------------------------------------------

import sys
import math
import numpy as np

breakValues = (2.5, 5.5, 8.5)
X = np.array([0,1,2,3,4,5,6,7,8,9])
Y = np.array([1,1,1,-1,-1,-1,1,1,1,-1])
W1 = np.array([0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1])

def Classifier25(x):
    if x <= 2.5:
        return 1
    else:
        return -1

def Classifier55(x):
    if x >= 5.5:
        return 1
    else:
        return -1

def Classifier85(x):
    if x <= 8.5:
        return 1
    else:
        return -1

def ClassifyArray(XArray, Classifier):
    YY = []
    for x in XArray:
        YY.append(Classifier(x))
    print(YY)
    return YY
def ErrorSum(YY):
    i = 0
    errorValue = 0;
    for y in YY:
        if y != Y[i]:
            errorValue += W1[i]
        i = i+1
    return errorValue

def ErrorAllSum(ExpressArray):
    i = 0
    errorValue = 0;
    for x in X:
        value = 0
        for express in ExpressArray:
            value += express[0] * express[1](x)
        if value > 0:
            value = 1
        else:
            value = -1
        if value != Y[i]:
            errorValue += 0.1
        i = i+1
    return errorValue

def SelectClassifierFunction(XArray):
    ClassifierArray = [Classifier25, Classifier55, Classifier85]
    errArray = []
    value = float('NaN')
    errMin = float('Inf')
    for classifier in ClassifierArray:
        #计算分类的结果值
        YY = ClassifyArray(XArray, classifier)
        #计算分类的错误率
        errorValue = ErrorSum(YY)
        errArray.append(errorValue)
        if errorValue < errMin:
            errMin = errorValue
            value = classifier
    print(errArray)
    print(value.__name__)
    return value

print(W1)

'''
print('--------------------------------')
classifier = SelectClassifierFunction(X)
#计算分类的结果值
G = ClassifyArray(X, classifier)
#计算分类的错误率
e = ErrorSum(G)
a = 0.5 * math.log((1-e)/e)
a = round(a, 4)
print(a)
W2 = W1*np.exp(-a*Y*np.array(G))
Zm = np.sum(W2)
#Zm = round(Zm, 4)
print(Zm)
W1 = W2 / Zm
print(W1)

print('--------------------------------')

W1 = np.array([0.0715,0.0715,0.0715,0.0715,0.0715,0.0715,0.1666,0.1666,0.1666,0.07151])
classifier = SelectClassifierFunction(X)
#计算分类的结果值
G = ClassifyArray(X, classifier)
#计算分类的错误率
e = ErrorSum(G)
a = 0.5 * math.log((1-e)/e)
a = round(a, 4)
print(a)
W2 = W1*np.exp(-a*Y*np.array(G))
Zm = np.sum(W2)
#Zm = round(Zm, 4)
print(Zm)
W1 = W2 / Zm
print(W1)

print('--------------------------------')

W1 = np.array([0.0455, 0.0455, 0.0455, 0.1667, 0.1667, 0.01667, 0.1060, 0.1060, 0.1060, 0.0455])
classifier = SelectClassifierFunction(X)
#计算分类的结果值
G = ClassifyArray(X, classifier)
#计算分类的错误率
e = ErrorSum(G)
a = 0.5 * math.log((1-e)/e)
a = round(a, 4)
print(a)
W2 = W1*np.exp(-a*Y*np.array(G))
Zm = np.sum(W2)
#Zm = round(Zm, 4)
print(Zm)
W1 = W2 / Zm
print(W1)
'''

errorAll = 100
ExpressArray = []
while errorAll > 0.1:
    print('--------------------------------')
    classifier = SelectClassifierFunction(X)
    #计算分类的结果值
    G = ClassifyArray(X, classifier)
    #计算分类的错误率
    e = ErrorSum(G)
    a = 0.5 * math.log((1-e)/e)
    a = round(a, 4)
    print('a:' + str(a))
    W2 = W1*np.exp(-a*Y*np.array(G))
    Zm = np.sum(W2)
    #Zm = round(Zm, 4)
    print(Zm)
    print('Zm:' + str(Zm))
    W1 = W2 / Zm
    print('W1:' + str(W1))
    ExpressArray.append([a,classifier])
    errorAll = ErrorAllSum(ExpressArray)
    print('errorAll:' + str(errorAll))

expressString = 'G(x) = sign( '
i = 0
for express in ExpressArray:
    if i > 0:
        expressString += ' + '
    expressString += str(express[0]) + ' * ' + express[1].__name__+'(x)'
    i += 1

expressString += ' )'
print('--------------------------------')
print('分类函数为：\n' + expressString)
print('--------------------------------')