BZOJ1478 Sgu282 Isomorphism

Problem A: Sgu282 Isomorphism

Time Limit: 15 Sec  Memory Limit: 64 MB
Submit: 172  Solved: 88
[Submit][Status][Discuss]

Description

给 定一个N 个结点的无向完全图（ 任意两个结点之间有一条边）， 现在你可以用 M 种颜色对这个图的每条边进行染色，每条边必须染一种颜色。 若两个已染色的图，其中一个图可以通过结点重新编号而与另一个图完全相同， 就称这两个染色方案相同。 现在问你有多少种本质不同的染色方法，输出结果 mod P。P 是一个大于N 的质数。

Input

仅一行包含三个数，N、M、P。

Output

仅一行，为染色方法数 mod P 的结果。

Sample Input

3 4 97

Sample Output

20

HINT

---

题解：

　　　一眼可以看出这是置换群吧，但是它要求的是边置换，开始感觉没什么思路，但是想想一条边由（u，v）两个点构成

　　　于是我们有了新的思路：考虑将点置换转换为边置换

　　　　

　　　我们可以发现点置换转化为的边置换同样具有相应的循环节

　　　于是考虑使用polya定理解决这个问题

　　　L：表示一个循环的大小； C：表示循环节的个数；

　　　首先对于一条边（u，v）它要分为两种情况：

　　　(1)u，v不在在同一个点循环，于是对于这条边所在的循环的大小为L_u-v=lcm（L_u,L_v），C_u-v=（L_u*L_v）/lcm（L_u,L_v）=gcd(L_u,L_v);

　　　(2) u，v在同一个点循环,于是分奇数和偶数进行讨论：

　　　　　一共C(L,2)条边 注：此处C为组合数

　　　　　1.奇数：Li是奇数，每个循环覆盖Li条边；循环节个数：

　　　　　2.偶数：Li是偶数，一个特例：覆盖Li/2条边的循环；循环节个数：

　　  (3)由上可知循环节个数：

　　　　•实际N!个点置换中，有多少个 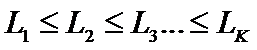    结构呢？

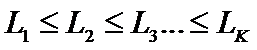　　　　•一个循环看成一个圆排列，现在要把N个人分配到k个长度分别为 的独立不相关圆排列中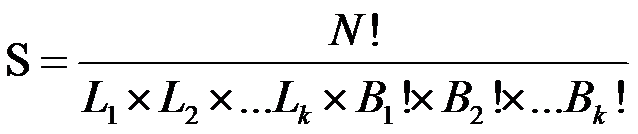

　　　　•因为有     L_i==L_j  的情况，设Bi为有多少个Lj=i

　　　　•总分配数为

　　 (4由上求出答案即可：

---

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<cstdio>
#define ll long long
#define N 70
using namespace std;
ll n,m,p;
ll num[N],l[N],bin[N];
ll ans;
ll read()
{
    ll x=,f=; char ch;
    while (ch=getchar(),ch<''||ch>'') if (ch=='-') f=-;
    while (x=x*+ch-'',ch=getchar(),ch>=''&&ch<='');
    return x*f;
}
int gcd(int a,int b){return b?gcd(b,a%b):a;
}
ll ksm(int x,int k){ll res=; for (int i=k; i; i>>=,x=1ll*x*x%p) if (i&) res=1ll*res*x%p; return res;
}
void cal(int k)
{
    ll s=;
    for (int i=; i<=n; i++) num[i]=;
    for (int i=; i<=k ;i++) num[l[i]]++;
    for (int i=; i<=k; i++) s=s*l[i]%p;
    for (int i=; i<=n; i++) s=s*bin[num[i]]%p;
    int c=;
    for (int i=; i<=k; i++)
    {
        c+=l[i]/;
        for (int j=i+; j<=k; j++) c+=gcd(l[i],l[j]);
    }
    ans=(ans+ksm(m,c)*bin[n]%p*ksm(s,p-)%p)%p;
}
void dfs(int x,int k,int last)
{
    if (x==n+) {cal(k-); return;}
    for (int i=; i<=last && x+i<=n+; i++)
    {
        l[k]=i; dfs(x+i,k+,i);
    }
}
int main()
{
    n=read(); m=read(); p=read();
    bin[]=; for (int i=; i<=n; i++) bin[i]=bin[i-]*i%p;
    dfs(,,n);
    printf("%lld\n",ans*ksm(bin[n],p-)%p);
    return ;
}