线性判别分析算法（LDA）

1. 问题

之前我们讨论的PCA、ICA也好，对样本数据来言，可以是没有类别标签y的。回想我们做回归时，如果特征太多，那么会产生不相关特征引入、过度拟合等问题。我们可以使用PCA来降维，但PCA没有将类别标签考虑进去，属于无监督的。

比如回到上次提出的文档中含有“learn”和“study”的问题，使用PCA后，也许可以将这两个特征合并为一个，降了维度。但假设我们的类别标签y是判断这篇文章的topic是不是有关学习方面的。那么这两个特征对y几乎没什么影响，完全可以去除。

再举一个例子，假设我们对一张100*100像素的图片做人脸识别，每个像素是一个特征，那么会有10000个特征，而对应的类别标签y仅仅是0/1值，1代表是人脸。这么多特征不仅训练复杂，而且不必要特征对结果会带来不可预知的影响，但我们想得到降维后的一些最佳特征（与y关系最密切的），怎么办呢？

2. 线性判别分析（二类情况）

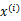回顾我们之前的logistic回归方法，给定m个n维特征的训练样例（i从1到m），每个对应一个类标签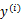。我们就是要学习出参数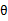，使得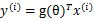（g是sigmoid函数）。

现在只考虑二值分类情况，也就是y=1或者y=0。

为了方便表示，我们先换符号重新定义问题，给定特征为d维的N个样例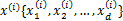，，其中有个样例属于类别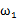，另外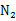个样例属于类别。

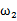现在我们觉得原始特征数太多，想将d维特征降到只有一维，而又要保证类别能够“清晰”地反映在低维数据上，也就是这一维就能决定每个样例的类别。

我们将这个最佳的向量称为w（d维），那么样例x（d维）到w上的投影可以用下式来计算

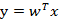
这里得到的y值不是0/1值，而是x投影到直线上的点到原点的距离。

当x是二维的，我们就是要找一条直线（方向为w）来做投影，然后寻找最能使样本点分离的直线。如下图：

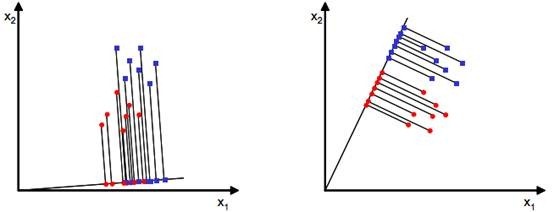
从直观上来看，右图比较好，可以很好地将不同类别的样本点分离。

接下来我们从定量的角度来找到这个最佳的w。

首先我们寻找每类样例的均值（中心点），这里i只有两个

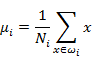
由于x到w投影后的样本点均值为

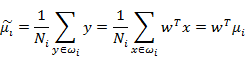
由此可知，投影后的的均值也就是样本中心点的投影。

什么是最佳的直线（w）呢？我们首先发现，能够使投影后的两类样本中心点尽量分离的直线是好的直线，定量表示就是：

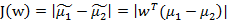
J(w)越大越好。

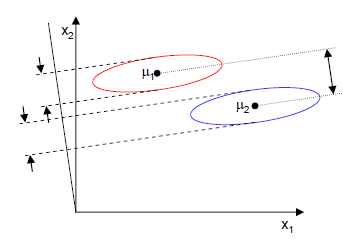
但是只考虑J(w)行不行呢？不行，看下图

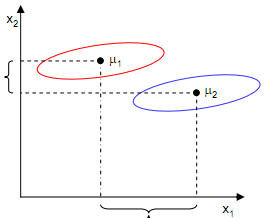
样本点均匀分布在椭圆里，投影到横轴x1上时能够获得更大的中心点间距J(w)，但是由于有重叠，x1不能分离样本点。投影到纵轴x2上，虽然J(w)较小，但是能够分离样本点。因此我们还需要考虑样本点之间的方差，方差越大，样本点越难以分离。

我们使用另外一个度量值，称作散列值（scatter），对投影后的类求散列值，如下

从公式中可以看出，只是少除以样本数量的方差值，散列值的几何意义是样本点的密集程度，值越大，越分散，反之，越集中。

而我们想要的投影后的样本点的样子是：不同类别的样本点越分开越好，同类的越聚集越好，也就是均值差越大越好，散列值越小越好。正好，我们可以使用J(w)和S来度量，最终的度量公式是

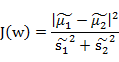
接下来的事就比较明显了，我们只需寻找使J(w)最大的w即可。

先把散列值公式展开

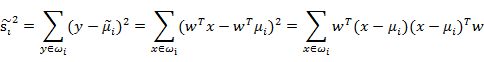
我们定义上式中中间那部分

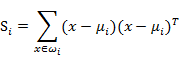
这个公式的样子不就是少除以样例数的协方差矩阵么，称为散列矩阵（scatter matrices）

我们继续定义

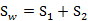
称为Within-class scatter matrix。

那么回到上面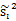的公式，使用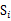替换中间部分，得

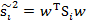
然后，我们展开分子

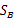称为Between-class scatter，是两个向量的外积，虽然是个矩阵，但秩为1。

那么J(w)最终可以表示为

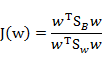
在我们求导之前，需要对分母进行归一化，因为不做归一的话，w扩大任何倍，都成立，我们就无法确定w。因此我们打算令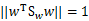，那么加入拉格朗日乘子后，求导

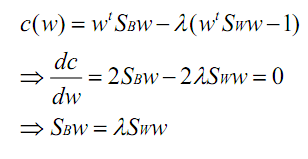
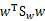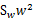其中用到了矩阵微积分，求导时可以简单地把当做看待。

如果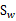可逆，那么将求导后的结果两边都乘以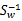，得

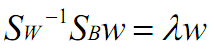
这个可喜的结果就是w就是矩阵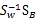的特征向量了。

这个公式称为Fisher linear discrimination。

等等，让我们再观察一下，发现前面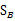的公式

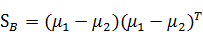
那么

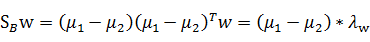
代入最后的特征值公式得

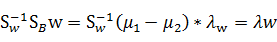
由于对w扩大缩小任何倍不影响结果，因此可以约去两边的未知常数和，得到

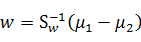
至此，我们只需要求出原始样本的均值和方差就可以求出最佳的方向w，这就是Fisher于1936年提出的线性判别分析。

看上面二维样本的投影结果图：

3. 线性判别分析（多类情况）

前面是针对只有两个类的情况，假设类别变成多个了，那么要怎么改变，才能保证投影后类别能够分离呢？

我们之前讨论的是如何将d维降到一维，现在类别多了，一维可能已经不能满足要求。假设我们有C个类别，需要K维向量（或者叫做基向量）来做投影。

将这K维向量表示为。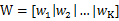

我们将样本点在这K维向量投影后结果表示为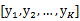，有以下公式成立

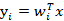
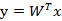
为了像上节一样度量J(w)，我们打算仍然从类间散列度和类内散列度来考虑。

当样本是二维时，我们从几何意义上考虑：

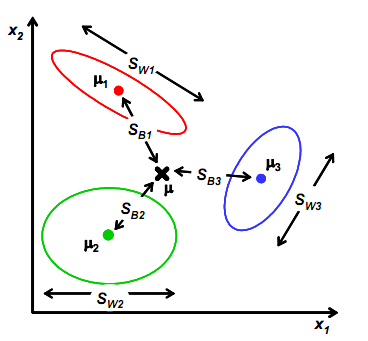
其中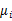和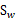与上节的意义一样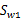，是类别1里的样本点相对于该类中心点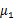的散列程度。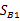变成类别1中心点相对于样本中心点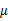的协方差矩阵，即类1相对于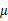的散列程度。

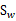为

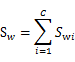
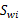的计算公式不变，仍然类似于类内部样本点的协方差矩阵

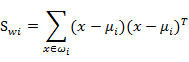
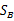需要变，原来度量的是两个均值点的散列情况，现在度量的是每类均值点相对于样本中心的散列情况。类似于将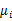看作样本点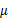，是均值的协方差矩阵，如果某类里面的样本点较多，那么其权重稍大，权重用Ni/N表示，但由于J(w)对倍数不敏感，因此使用Ni。

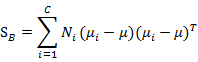
其中

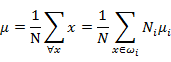
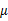是所有样本的均值。

上面讨论的都是在投影前的公式变化，但真正的J(w)的分子分母都是在投影后计算的。下面我们看样本点投影后的公式改变：

这两个是第i类样本点在某基向量上投影后的均值计算公式。

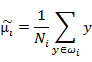
下面两个是在某基向量上投影后的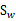和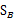

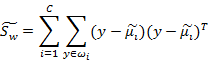
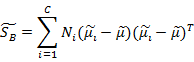
其实就是将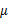换成了。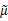

综合各个投影向量（w）上的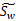和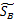，更新这两个参数，得到

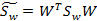
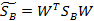
W是基向量矩阵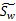，是投影后的各个类内部的散列矩阵之和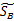，是投影后各个类中心相对于全样本中心投影的散列矩阵之和。

回想我们上节的公式J(w)，分子是两类中心距，分母是每个类自己的散列度。现在投影方向是多维了（好几条直线），分子需要做一些改变，我们不是求两两样本中心距之和（这个对描述类别间的分散程度没有用），而是求每类中心相对于全样本中心的散列度之和。

然而，最后的J(w)的形式是

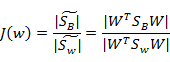
由于我们得到的分子分母都是散列矩阵，要将矩阵变成实数，需要取行列式。又因为行列式的值实际上是矩阵特征值的积，一个特征值可以表示在该特征向量上的发散程度。因此我们使用行列式来计算（此处我感觉有点牵强，道理不是那么有说服力）。

整个问题又回归为求J(w)的最大值了，我们固定分母为1，然后求导，得出最后结果（我翻查了很多讲义和文章，没有找到求导的过程）

与上节得出的结论一样

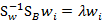
最后还归结到了求矩阵的特征值上来了。首先求出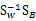的特征值，然后取前K个特征向量组成W矩阵即可。

注意：由于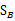中的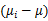 秩为1，因此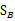的秩至多为C（矩阵的秩小于等于各个相加矩阵的秩的和）。由于知道了前C-1个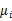后，最后一个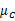可以有前面的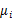来线性表示，因此的秩至多为C-1。那么K最大为C-1，即特征向量最多有C-1个。特征值大的对应的特征向量分割性能最好。

由于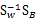不一定是对称阵，因此得到的K个特征向量不一定正交，这也是与PCA不同的地方。

4. 实例

将3维空间上的球体样本点投影到二维上，W1相比W2能够获得更好的分离效果。

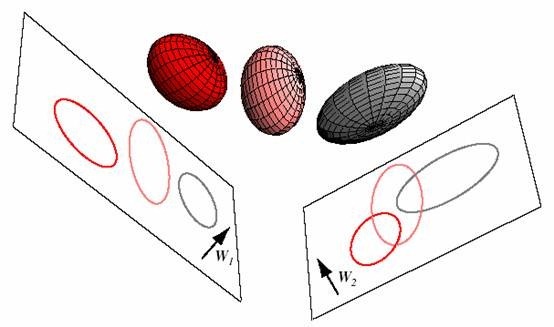
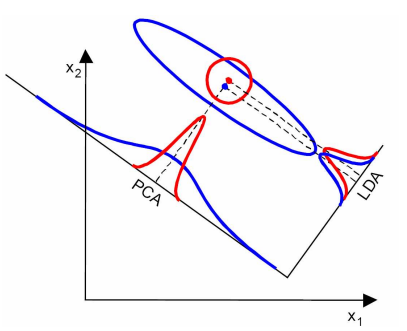
PCA与LDA的降维对比：

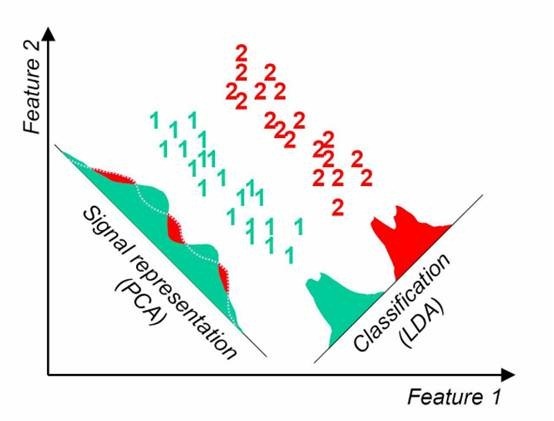
PCA选择样本点投影具有最大方差的方向，LDA选择分类性能最好的方向。

LDA既然叫做线性判别分析，应该具有一定的预测功能，比如新来一个样例x，如何确定其类别？

拿二值分来来说，我们可以将其投影到直线上，得到y，然后看看y是否在超过某个阈值y0，超过是某一类，否则是另一类。而怎么寻找这个y0呢？

看

根据中心极限定理，独立同分布的随机变量和符合高斯分布，然后利用极大似然估计求

然后用决策理论里的公式来寻找最佳的y0，详情请参阅PRML。

这是一种可行但比较繁琐的选取方法，可以看第7节（一些问题）来得到简单的答案。

5. 使用LDA的一些限制

1、 LDA至多可生成C-1维子空间

LDA降维后的维度区间在[1,C-1]，与原始特征数n无关，对于二值分类，最多投影到1维。

2、 LDA不适合对非高斯分布样本进行降维。

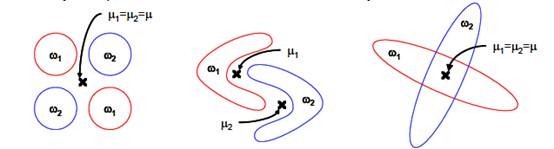
上图中红色区域表示一类样本，蓝色区域表示另一类，由于是2类，所以最多投影到1维上。不管在直线上怎么投影，都难使红色点和蓝色点内部凝聚，类间分离。

3、 LDA在样本分类信息依赖方差而不是均值时，效果不好。

上图中，样本点依靠方差信息进行分类，而不是均值信息。LDA不能够进行有效分类，因为LDA过度依靠均值信息。

4、 LDA可能过度拟合数据。

6. LDA的一些变种

1、 非参数LDA

非参数LDA使用本地信息和K临近样本点来计算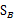,使得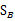是全秩的，这样我们可以抽取多余C-1个特征向量。而且投影后分离效果更好。

2、 正交LDA

先找到最佳的特征向量，然后找与这个特征向量正交且最大化fisher条件的向量。这种方法也能摆脱C-1的限制。

3、 一般化LDA

引入了贝叶斯风险等理论

4、 核函数LDA

将特征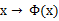，使用核函数来计算。

7. 一些问题

上面在多值分类中使用的

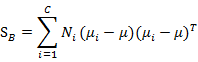
是带权重的各类样本中心到全样本中心的散列矩阵。如果C=2（也就是二值分类时）套用这个公式，不能够得出在二值分类中使用的。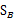

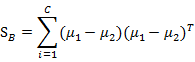
因此二值分类和多值分类时求得的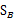会不同，而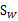意义是一致的。

对于二值分类问题，令人惊奇的是最小二乘法和Fisher线性判别分析是一致的。

下面我们证明这个结论，并且给出第4节提出的y0值得选取问题。

回顾之前的线性回归，给定N个d维特征的训练样例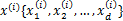（i从1到N），每个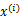对应一个类标签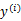。我们之前令y=0表示一类，y=1表示另一类，现在我们为了证明最小二乘法和LDA的关系，我们需要做一些改变

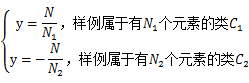
就是将0/1做了值替换。

我们列出最小二乘法公式

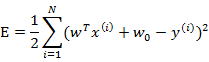
w和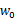是拟合权重参数。

分别对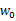和w求导得

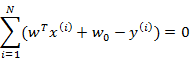
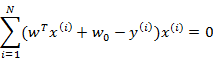
从第一个式子展开可以得到

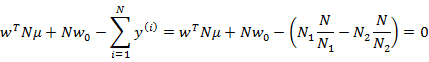
消元后，得

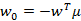
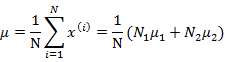
可以证明第二个式子展开后和下面的公式等价

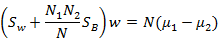
其中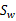和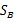与二值分类中的公式一样。

由于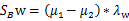

因此，最后结果仍然是

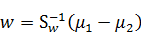
这个过程从几何意义上去理解也就是变形后的线性回归（将类标签重新定义），线性回归后的直线方向就是二值分类中LDA求得的直线方向w。

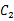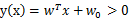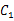好了，我们从改变后的y的定义可以看出y>0属于类，y<0属于类。因此我们可以选取y0=0，即如果，就是类，否则是类。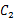

写了好多，挺杂的，还有个topic模型也叫做LDA，不过名字叫做Latent Dirichlet Allocation，第二作者就是Andrew Ng大牛，最后一个他导师Jordan泰斗了，什么时候拜读后再写篇总结发上来吧。