机器学习：集成学习（Bagging、Pasting）

一、集成学习算法的问题

• 可参考：模型集成（Enxemble）
• 博主：独孤呆博

• 思路：集成多个算法，让不同的算法对同一组数据进行分析，得到结果，最终投票决定各个算法公认的最好的结果；

• 弊端：虽然有很多机器学习的算法，但是从投票的角度看，仍然不够多；如果想要有效果更好的投票结果，最好有更多的算法参与；（概率论中称大数定理）

• 方案：创建更多的子模型，集成更多的子模型的意见；

1. 子模型之间要有差异，不能一致；

二、如何创建具有差异的子模型

　1）创建思路、子模型特点

• 思路：每个子模型只使用样本数据的一部分；（也就是说，如果一共有 500 个样本数据，每个子模型只看 100 个样本数据，每个子模型都使用同一个算法）

• 特点

1. 由于将样本数据平分成 5 份，每份 100 个样本数据，每份样本数据之间有差异，因此所训练出的 5 个子模型之间也存在差异；
2. 5 个子模型的准确率低于使用全部样本数据所训练出的模型的准确率；
3. 实际应用中，每个子模型的准确率有高有低，甚至有些子模型的准确率低于 50%；

• 集成的众多模型中，并不要求子模型有更高的准确率，只要子模型的准确率大于 50%，在集成的模型当中，随着子模型数量的增加，集成学习的整体的准确率升高；

• 原因分析见下图：

• 

• 

　2）怎么分解样本数据给每个子模型？

• 放回取样（Bagging）

1. 每个子模型从所有的样本数据中随机抽取一定数量的样本，训练完成后将数据放回样本数据中，下个子模型再从所有的样本数据中随机抽取同样数量的子模型；
2. 机器学习领域，放回取样称为 Bagging；统计学中，放回取样称为 bootstrap；

• 不放回取样（Pasting）
• 500 个样本数据，第一个子模型从 500 个样本数据中随机抽取 100 个样本，第二个子模型从剩余的 400 个样本中再随机抽取 100 个样本；

• 通常采用 Bagging 的方式

• 原因：

1. 可以训练更多的子模型，不受样本数据量的限制；
2. 在 train_test_split 时，不那么强烈的依赖随机；而 Pasting 的方式，会首随机的影响；

• Pasting 的随机问题：Pasting 的方式等同于将 500 个样本分成 5 份，每份 100 个样本，怎么分，将对子模型有较大影响，进而对集成系统的准确率有较大影响；

　3）实例创建子模型

• scikit-learn 中默认使用 Bagging 的方式生成子模型；

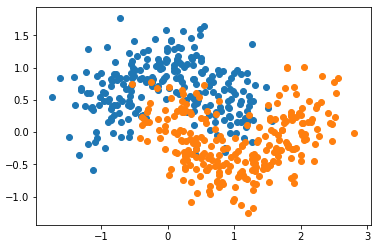
• 模拟数据集

  import numpy as np
  import matplotlib.pyplot as plt
  from sklearn import datasets
  from sklearn.model_selection import train_test_split
   
  X, y = datasets.make_moons(n_samples=500, noise=0.3, random_state=42)
   
  X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
   
  plt.scatter(X[y==0, 0], X[y==0, 1])
  plt.scatter(X[y==1, 0], X[y==1, 1])
  plt.show()

  

• 使用 Bagging 取样方式，决策树算法 DecisionTreeClassifier 集成 500 个子模型

  from sklearn.tree import DecisionTreeClassifier
  from sklearn.ensemble import BaggingClassifier
   
  bagging_clf = BaggingClassifier(DecisionTreeClassifier(),
                                 n_estimators=500, max_samples=200,
                                 bootstrap=True)
   
  bagging_clf.fit(X_train, y_train)
  bagging_clf.score(X_test, y_test)
  # 准确率：0.904

• BaggingClassifier() 的参数：

1. DecisionTreeClassifier()：表示需要根据什么算法生产子模型；
2. n_estimators=500：集成 500 个子模型；
3. max_samples=100：每个子模型看 100 个样本数据；
4. bootstrap=True：表示采用 Bagging 的方式从样本数据中取样；（默认方式）
5. bootstrap=False：表示采用 Pasting 的方式从样本数据中取样；

三、其它

• 老师指点：

1. 机器学习的过程没有一定之规，没有soft永远比hard好的结论（如果是那样，我们实现的接口就根本不需要hard这个选项了；
2. 并不是说子模型数量永远越多越好，一切都要根据数据而定，对于一组具体的数据，如论是soft还是hard，亦或是子模型数量，都是超参数，在实际情况都需要根据数据进行一定的调节。
3. 在机器学习的世界里，在训练阶段，并不是准确率越高越好。因为准确率高有可能是过拟合。应该是“越真实越好”。

• 所谓的真实是指结果要能“真实”的反应训练数据和结果输出的关系。

• 在真实的数据中，使用验证数据集是很重要的：）