【转载】最长回文字符串(manacher算法)

原文转载自：http://blog.csdn.net/lsjseu/article/details/9990539

偶然看见了人家的博客发现这么一个问题，研究了一下午， 才发现其中的奥妙。Stupid。

题目描述：

回文串就是一个正读和反读都一样的字符串，比如“level”或者“noon”等等就是回文串。

回文子串，顾名思义，即字符串中满足回文性质的子串。

给出一个只由小写英文字符a,b,c…x,y,z组成的字符串，请输出其中最长的回文子串的长度。

输入：

输入包含多个测试用例，每组测试用例输入一行由小写英文字符a,b,c…x,y,z组成的字符串，字符串的长度不大于200000。

输出：

对于每组测试用例，输出一个整数，表示该组测试用例的字符串中所包含的的最长回文子串的长度。

样例输入：

abab
bbbb
abba

样例输出：

3
4
4

思路：

回文串包括奇数长的和偶数长的，一般求的时候都要分情况讨论，这个算法做了个简单的处理把奇偶情况统一了。原来是奇数长度还是奇数长度，偶数长度还是偶数长度。

算法的基本思路是这样的，把原串每个字符中间用一个串中没出现过的字符分隔#开来(统一奇偶)，同时为了防止越界，在字符串的首部也加入一个特殊符$，但是与分隔符不同。同时字符串的末尾也加入’\0’.

算法的核心：用辅助数组p记录以每个字符为核心的最长回文字符串半径。也就是p[i]记录了以str[i]为中心的最长回文字符串半径。p[i]最小为1，此时回文字符串就是字符串本身。

  先看个例子：

  原串：        w aa bwsw f d
  新串：     $ # w# a # a # b# w # s # w # f # d #

辅助数组P： 1 2 1 2 3 2 1 2 1 2 1 4 1 2 1 2 1 2 1

首先看代码（借助http://blog.csdn.net/thyftguhfyguj/article/details/9531149）：

 #include <stdio.h>
    #include <iostream>
    using namespace std;  

    char s[200002];
    char str[400010];
    int p[400010];    

    int min(int a,int b){
        return a < b ? a : b;
    }    

    int pre(){
        int i,j = 0;
        str[j++] = '$';//加入字符串首部的字符串
        for(i = 0;s[i];i++){
            str[j++] = '#';  //分隔符
            str[j++] = s[i];
        }
        str[j++] = '#';
        str[j] = '\0';  //尾部加'\0'
        cout<<str<<endl;
        return j;
    }    

    void manacher(int n){
        int mx = 0,id,i;
        p[0] = 0;
        for(i = 1;i < n;i++){
            if(mx > i)  //在这个之类可以借助前面算的一部分
                p[i] = min(mx - i,p[2 * id - i]); //p[2*id-i]表示j处的回文长度
            else  //如果i大于mx，则必须重新自己算
                p[i] = 1;
            while(str[i - p[i]] == str[i + p[i]])  //算出回文字符串的半径
                p[i]++;
            if(p[i] + i > mx){  //记录目前回文字符串扩展最长的id
                mx = p[i] + i;
                id = i;
            }
        }
    }    

    int main(int argc, char const *argv[]){    

        while(scanf("%s",s) != EOF){
            int n = pre();
            manacher(n);
            int ans = 0,i;
            for(i = 1;i < n;i++)
                if(p[i] > ans)
                    ans = p[i];
            printf("%d\n",ans - 1);
        }
        return 0;
    }   

上面的程序说明：pre()函数对给定字符串进行预处理，也就是加分隔符。

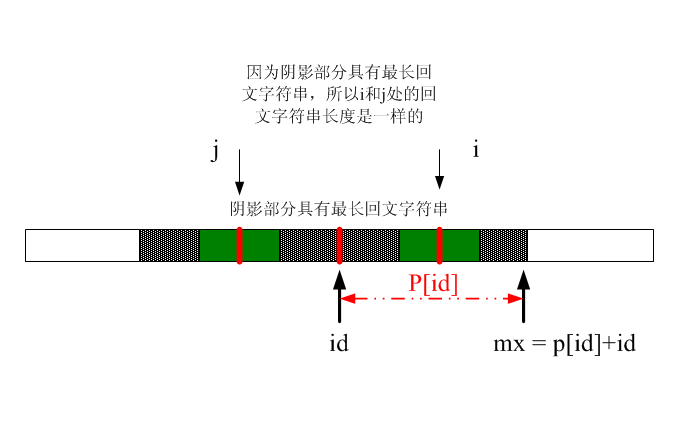
上面几个变量说明：id记录具有遍历过程中最长半径的回文字符串中心字符串。mx记录了具有最长回文字符串的右边界。看下面这个图（注意，j为i关于id对称的点，j = 2*id - i）：

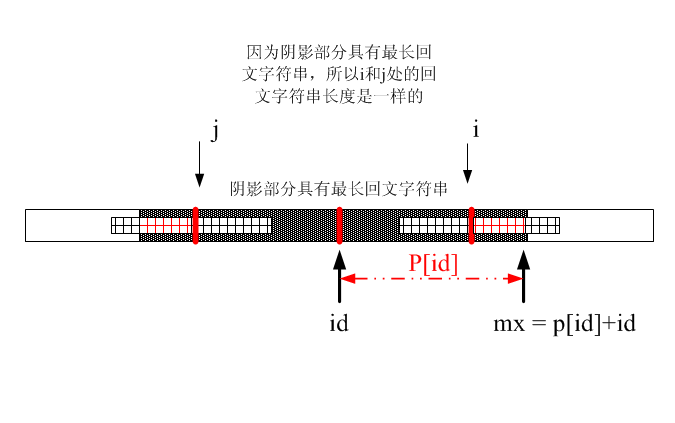
但是p[i] = p[j]是没有错的，但是这里有个问题，就是i的一部分超出阴影部分，这就不对了。请看下图（为了看得更清楚，下面子串用细条纹表示）：

此时，根据对称型只能得出p[i]和p[j]红色阴影部分是相等的，这就为什么有取最小值这个操作：

   if(mx > i)  //在这个之类可以借助前面算的一部分
        p[i] = min(mx - i,p[2 * id - i]);  

下面代码就很容易看懂了。

最后遍历一遍p数组，找出最大的p[i]-1就是所求的最长回文字符串长度，下面证明一下：

（1）因为p[i]记录插入分隔符之后的回文字符串半径，注意插入分隔符之后的字符串中的回文字符串肯定是奇数长度，所以以i为中心的回文字符串长度为2*p[i]-1。

例如：

bb=>#b#b#
bab=>#b#a#a#b#

2）注意上面两个例子的关系。#b#b#减去一个#号的长度就是原来的2倍。即((2*p[i]-1)-1)/2 = p(i)-1，得证。

算法的有效比较次数为MaxId 次，所以说这个算法的时间复杂度为O(n)。