cnn softmax regression bp求导

内容来自ufldl，代码参考自tornadomeet的cnnCost.m

1.Forward Propagation

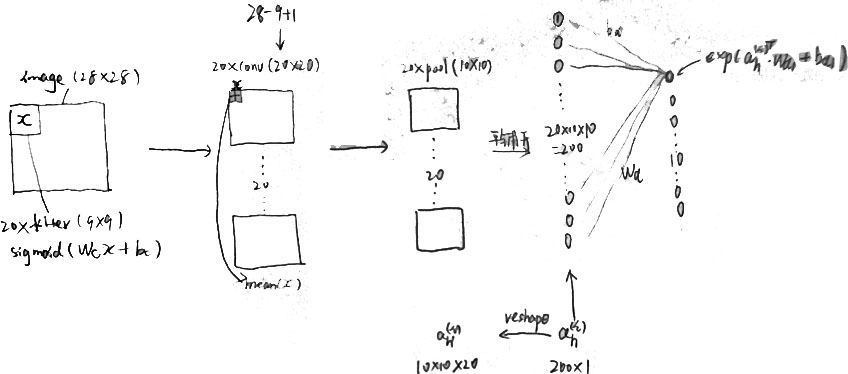
convolvedFeatures = cnnConvolve(filterDim, numFilters, images, Wc, bc); %对于第一个箭头
activationsPooled = cnnPool(poolDim, convolvedFeatures);%对应第二个箭头

%对应第3个箭头，即平铺开
activationsPooled = reshape(activationsPooled,[],numImages);

%开始计算softmax后属于各类的概率
probs = zeros(numClasses,numImages);

%Wd=(numClasses,hiddenSize),probs的每一列代表一个输出
%M=Wd*ah+bd
M = Wd*activationsPooled+repmat(bd,[1,numImages]);
%这步可以省略，可以这么做的原因是 exp(a+b)=exp(a)exp(b)
M = bsxfun(@minus,M,max(M,[],1));
%M=exp(Wd*ah+bd)
M = exp(M);
%normalize
probs = bsxfun(@rdivide, M, sum(M));

2.Back propagation

% 首先需要把labels弄成one-hot编码
%对应图片中的I
groundTruth = full(sparse(labels, 1:numImages, 1));

%P-I
delta_d = -(groundTruth-probs);
%ah(P-I) ，不同处为后面加上了正规项的导数
Wd_grad = (1./numImages)*delta_d*activationsPooled'+lambda*Wd;
bd_grad = (1./numImages)*sum(delta_d,2); %注意这里是要求和

%对应图中reshape右边的   J对ah求导
delta_s = Wd'*delta_d;
delta_s=reshape(delta_s,outputDim,outputDim,numFilters,numImages);

%对应途中    1/4，delta_s的每个分量，都扩展为4个
for i=1:numImages
    for j=1:numFilters
        delta_c(:,:,j,i) = (1./poolDim^2)*kron(squeeze(delta_s(:,:,j,i)), ones(poolDim));
    end
end
%对于左下方，但此时ximage还没有乘上去
delta_c = convolvedFeatures.*(1-convolvedFeatures).*delta_c;

for i=1:numFilters
    Wc_i = zeros(filterDim,filterDim);
    for j=1:numImages
%此处conv2非常巧妙
        Wc_i = Wc_i+conv2(squeeze(images(:,:,j)),rot90(squeeze(delta_c(:,:,i,j)),2),'valid');
    end
   % Wc_i = convn(images,rot180(squeeze(delta_c(:,:,i,:))),'valid');
    % add penalize
    Wc_grad(:,:,i) = (1./numImages)*Wc_i+lambda*Wc(:,:,i);

    bc_i = delta_c(:,:,i,:);
    bc_i = bc_i(:);
    bc_grad(i) = sum(bc_i)/numImages;
end

上面conv2的正确性，可以用下面方法验证

A=rand(9,9);
B=rand(3,3);
c1=conv2(A,B,'valid');

B=zeros(3);
for i=1:7
    for j=1:7
        B=B+(A(i:i+2,j:j+2)*c1(i,j));
    end
end
%看到B和conv2结果相同
conv2(A,rot90(c1,2),'valid')
B