Dijkstra(迪杰斯特拉)源最短路径 小白说明

 

Dijkstra算法,书上其实说的很简洁,仔细看,仔细思考是会理解的.但要先理解几条引论和推理.

而自己思考的思路在不需要任何推理只从贪心思路出发,和Dijkstra有所不同,但本质一样,那么自己按照理解,试着慢慢讲下.

一,问题:

从某个源点,到其他各点的最短路径.

注意,不要想成某一个点,到某个点的最短路径.这样的话不太好推导出思路。

某个源点,到其他各点的最短路径.这样的思路反而好推导出，反正所有点都计算出来了。某点到某点就是其中一条而已。，

二,分析.

先抛弃书中所有关于最短路径的引理,定理,公理....

先看图.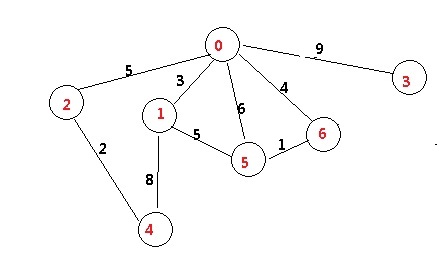

　　要找到从0点.到所有点的最短路径.

　　假如,小明,站在0点.他很渴,天气很热,再不喝水要渴死,而每个其他点,都有一瓶水,点和点之间的交通工具还不一样,有的是汽车,有的还必须走路.

　　假设这里的权值代表两点之间所花费的时间,比如0 ~3中间的数字6, 表示.从0到3要6个小时的慢车.

　　打开地图一看,到底哪个是最短啊.他想喝3点的水,发现要9个小时. 居然比 先到2,再到4, 7个小时还长,那么去4吧.你当小明傻啊.到了2点,不喝水,还去4点.

　　所以小明得到一个常识,对于第一瓶水,需要中转点而到达的目的点肯定不是花费时间最少的,最起码可以喝那个中转站的水.

　　直连的点话,看看哪个点花费的时间少.  1点最少,只要3个小时.

　　废话少说,小明直接从0做车到1,花费3个小时,喝到了第一瓶水,刚喝完水,小明被时光机, 卟的一声,居然传回了0点.(因为我们要从0开始,找出到所有点的最短路径,所以小明被传送了.)

　　因为小明还是很渴,天气依然很热,再不喝水要渴死.

　　那么下一个最近的点在哪里?

　　小明开始思索, 1点是和0直连最近的.已经被我喝掉了.那么舍去1点,第二近的直连点是不是最近的呢?

　　先看看.发现了是6点.要4个小时.

　　其他直连点先全部抛弃,因为这个时候6点是直连点最近的了.

　　还有没有比4个小时更短的?有,是之前的1点,只要3个小时,但喝掉了.

　　小明思索一会,有答案了,唯一可能的是,如果原来1点,离它很近的地方有顶点.那么有可能比6点近.

　　看看地图,1可以到4和5.时间是5和8. 总时间就是 3+5和3+8.明显比4个小时长.

　　小明马上又坐车从0点到了6点.喝光水,毫无疑问, 卟的一声小明被时光机,又传回了0点.

　　不过有了上次的思考.

　　小明有了初步总结.

　　下一个最近的可能是2种方案中找一个

　　　　1)和0直连的点,但要除去1,和6.也就是和0直连的 第3近的点.

　　　　2)从最早的的1点出发,所能到达的点,虽然上次排除了,但说不定这次和第3近的点有的一拼.

　　正要查地图的时候.小明突然想到. 6点是第二近的点.说不定从6点出发,也有比 直连第3近的点更短呢.

　　终于,小明整理出了一个方案.

　　用一个数组MinRD[]  ,存放已知最短路径.

　　用另外一个数组noGet[],存放 所有点 减去 所有最短路径的终点.

　　每次从最短路径MinRD[]中,查询每条最短路径的终点. 再写下这些终点,到 未曾到达的点的权直.再找出最小的.

　　　　这里要想明白, 假如有一条最短路径经过了好几个点,如 0->1->3->6->7. 小明最后一次喝掉了7点的水,

也意味着,他之前喝掉了6点的水,也就是0->1->3->6是一个最短路径,

0->1->3->6->7是从0->1->3->6这个最短路径,由6顶点和其他最短路径的顶点通过残酷的比较中选出 来的.

这其实就是最优路径的的一个引论,最短路径,中间的路径也是最短路径.喝水喝出了引论.

　　不厌其烦的,我要写下每次程序运行的过程.

1)第一次找水.

已知最短路径

这个是原点,默认放入.

还未到达过的

1,2,3,4,5,6

只有一个终点0. 从终点出发,和还未到达过的点组成弧,找到最断的.

比较 v(,1),v(0,2),,v(0,3),v(0,4),v(0,5),v(0,6)

0->1最短,加入到最短路径集合中.

2)

已知最短路径

0->

还未到达过的

2,3,4,5,6

第一个最短路径的终点是0.第二条最短路径的终点是1

从终点0和1出发,和还未到达过的点组成弧,找到最断的.

比较  v(,2),,v(0,3),v(0,4),v(0,5),v(0,6),

v(,2),v(1,3),v(1,4),v(1,5),v(1,6)

0->6 最短,加入到最短路径集合中

3)

已知最短路径

0,

0->1                第一次找到的.

0->6                第二次找到的.

还未到达过的

2,3,4,5

比较  v(0,2),,v(0,3),v(0,4),v(0,5)

v(1,2),v(1,3),v(1,4),v(1,5)

　　　v(6,2),v(6,3),v(6,4),v(6,5)

最优路径终点0,1,6,

0->6->5 和 0->2 一样,

根据程序判断顺序,会加入其中一个,下次查找会加入另外一个. 也可以修改程序,让他们一次加入

c  代码如下(代码可读性一般)

struct Minroads
{
    int *road;
    int length;
    int cost;
};

int main()
{
    //临街矩阵，直接写出，就不用程序生成了，数字表示2点间弧的权直，-1表示2点不能直达。
    int matrix[][]={
    ,,,,-,,,
    ,,-,-,,,-,
    ,-,,-,,-,-,
    ,-,-,,-,-,-,
    -,,,-,,-,-,
    ,,-,-,-,,,
    ,-,-,-,-,,
    };

    struct Minroads MinRD[];//初始化最短路径数组
    int i=;
    for(i=;i<;i++)
    {
        MinRD[i].road=malloc(sizeof(int)*);
        MinRD[i].road[]=;
        MinRD[i].cost=;
        MinRD[i].length=;
    }

    int noGet[]={,,,,,,};//初始化未曾到达的顶点集合。

    MinRD[].road[]=;//把源点自己（起点）作为第一条最短路径加入最短路径集合（包含1个顶。权直和为0）
    MinRD[].length=;
    MinRD[].cost=;

    noGet[]=-;// 简单的把到达的点，标记为-1，0加入就把索引为0的数值改为-1。当nouse的元素全部为-1。那就全部到达。
    int get_count=;//

    //从每条已知的最短路径出发，走一步看看。比较所有产生的新路径，看看谁最短。
    //程序描述就是找出 ，minrd中，每个road的权直，加上，这条road的顶点到noGet中所有顶点的权直中最小的。
    while(get_count<)
    {
        int i_noget,i_shortest;
        int temp_short=0x7fffffff;//int 是有符号数，最高位为0，表示最大正数，
        int temp_s, tmep_d;
        for(i_shortest=;i_shortest<;i_shortest++)//所有最短路径
        {
            if(MinRD[i_shortest].length!=)//
            {
                for(i_noget=;i_noget<;i_noget++)//未曾到达的顶点
                {
                    if(noGet[i_noget]!=-)
                    {
                        int x;
                        x=MinRD[i_shortest].road[MinRD[i_shortest].length-];//最短路径的顶点
                        int y=noGet[i_noget];
                        int newshort;
                        if(matrix[x][y]!=-)
                        {
                            newshort=MinRD[i_shortest].cost+matrix[x][y];
                        }
                        else
                        {
                            newshort=0x7fffffff;
                        }
                        if(newshort<=temp_short)
                        {
                            temp_short=newshort;
                            temp_s=i_shortest;
                            tmep_d=i_noget;
                        }
                    }
                }
            }
        }

        int i_copy;
        for(i_copy=;i_copy<MinRD[temp_s].length;i_copy++)
        {
            MinRD[get_count].road[i_copy]=MinRD[temp_s].road[i_copy];
        }
        MinRD[get_count].road[i_copy]=tmep_d;

        MinRD[get_count].length=MinRD[temp_s].length+;
        MinRD[get_count].cost+=temp_short;

        noGet[tmep_d]=-;

        get_count++;
    }

    int i_print;
    for(i=;i<;i++)
    {
        for(i_print=;i_print<MinRD[i].length;i_print++)
        {
            if(i_print!=MinRD[i].length-)
            {
                printf("%d->",MinRD[i].road[i_print]);
            }
            else
            {
                printf("%d",MinRD[i].road[i_print]);
            }

        }
        printf("  cost:%d",MinRD[i].cost);
        printf("\n");
    }
}

结果:

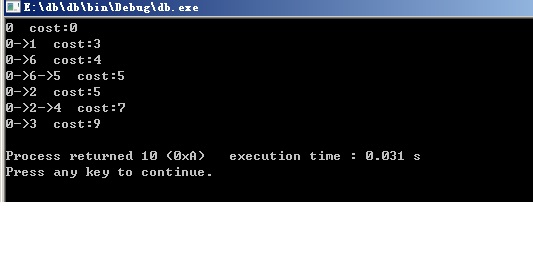
再次注意这里

0->6->5.这条最优路径找出来的话。上面必定有0->6这条最优路径。

闭着眼睛想一下，0->6->5是最优的话，没有理由，0—>6不是。如果0->6不是，而是0->x.那么,0->x->5,肯定比0->6->5更短。

Dijkstra(迪杰斯特拉)，是每次加入一条最短路径，那么更新   每个未处理的点    到     最短路径的顶点集合  的最短路径直。 选出最小的那个直。

注意当加入第一个原点的时候,本身的权直就相当于更新过一遍.

因为更新过,

能体现出动态调整的思路。

而我们的思路

体现的是贪心算法的思路。省掉了更新的步骤,每次重新计算所有的点.所以导致比Dijkstra运算量稍微大点。

不过自己推导出来，并能理解的，总感觉更亲切。

下篇看看怎么更容易理解的方式写出Dijkstra

几年后翻回来看。其实自己的想出来的思路，完全正确。就是贪心思路。

而Dijkstra是贪心+动态。当年用贪心想到就结束了。没有继续优化，保存中间值，否则就是Dijkstra算法了。

夸奖一下自己很难吗？比心。