2017 ACM-ICPC 亚洲区（南宁赛区）网络赛

02Train Seats Reservation

只看题面

33.87%
1000ms
131072K

You are given a list of train stations, say from the station 11 to the station 100100.

The passengers can order several tickets from one station to another before the train leaves the station one. We will issue one train from the station 11 to the station 100100 after all reservations have been made. Write a program to determine the minimum number of seats required for all passengers so that all reservations are satisfied without any conflict.

Note that one single seat can be used by several passengers as long as there are no conflicts between them. For example, a passenger from station 11 to station 1010 can share a seat with another passenger from station 3030 to 6060.

Input Format

Several sets of ticket reservations. The inputs are a list of integers. Within each set, the first integer (in a single line) represents the number of orders, nn, which can be as large as 10001000. After nn, there will be nn lines representing the nnreservations; each line contains three integers s, t, ks,t,k, which means that the reservation needs kk seats from the station ss to the station tt.These ticket reservations occur repetitively in the input as the pattern described above. An integer n = 0n=0 (zero) signifies the end of input.

Output Format

For each set of ticket reservations appeared in the input, calculate the minimum number of seats required so that all reservations are satisfied without conflicts. Output a single star '*' to signify the end of outputs.

样例输入

样例输出

题目来源

2017 ACM-ICPC 亚洲区（南宁赛区）网络赛

这个B是我的暴力扫描线做得不太好，我承认，我是个sb，本来卡long long，后来卡扫描线，可以先下后上嘛，所以是左闭右开区间

#include <bits/stdc++.h>

using namespace std;

const int N=;

int n,a[N],b[N];

int main()

{

    while(~scanf("%d",&n))

    {

        if(!n)

        {

            printf("*\n");

            break;

        }

        memset(a,,sizeof(a));

        memset(b,,sizeof(b));

        for(int i=; i<n; i++)

        {

            int l,r,x;

            scanf("%d%d%d",&l,&r,&x);

            a[l]+=x;

            b[r]+=x;

        }

        long long f=,ma=;

        for(int i=; i<=; i++)

        {

            f-=b[i];

            f+=a[i];

            ma=max(f,ma);

        }

        printf("%lld\n",ma);

    }

    return ;

}

Overlapping Rectangles

问答

只看题面

37.67%
1000ms
131072K

There are nn rectangles on the plane. The problem is to find the area of the union of these rectangles. Note that these rectangles might overlap with each other, and the overlapped areas of these rectangles shall not be counted more than once. For example, given a rectangle AA with the bottom left corner located at (0, 0)(0,0) and the top right corner at (2, 2)(2,2), and the other rectangle BB with the bottom left corner located at (1,1)(1,1) and the top right corner at (3,3)(3,3), it follows that the area of the union of AA and BB should be 77, instead of 88.

Although the problem looks simple at the first glance, it might take a while to figure out how to do it correctly. Note that the shape of the union can be very complicated, and the intersected areas can be overlapped by more than two rectangles.

Note:

(1) The coordinates of these rectangles are given in integers. So you do not have to worry about the floating point round-off errors. However, these integers can be as large as 1,000,0001,000,000.

(2) To make the problem easier, you do not have to worry about the sum of the areas exceeding the long integer precision. That is, you can assume that the total area does not result in integer overflow.

Input Format

Several sets of rectangles configurations. The inputs are a list of integers. Within each set, the first integer (in a single line) represents the number of rectangles, n, which can be as large as 10001000. After n, there will be n lines representing the n rectangles; each line contains four integers <a, b, c, d><a,b,c,d> , which means that the bottom left corner of the rectangle is located at (a, b)(a,b), and the top right corner of the rectangle is located at (c, d)(c,d). Note that integers aa, bb, cc, dd can be as large as 1,000,0001,000,000.

These configurations of rectangles occur repetitively in the input as the pattern described above. An integer n = 0n=0 (zero) signifies the end of input.

Output Format

For each set of the rectangles configurations appeared in the input, calculate the total area of the union of the rectangles. Again, these rectangles might overlap each other, and the intersecting areas of these rectangles can only be counted once. Output a single star '*' to signify the end of outputs.

样例输入

样例输出

题目来源

2017 ACM-ICPC 亚洲区（南宁赛区）网络赛

这个F网上直接有代码啊，直接拉过看来就行的，暴力扫描线肯定不行。线段树搞一下

#include<stdio.h>

#include<string.h>

#include<algorithm>

#define ls i<<1

#define rs i<<1|1

#define m(i) ((q[i].l + q[i].r)>>1)

using namespace std;

typedef long long ll;

const int N = ;

struct Edge

{

    double l,r;

    double h;

    int f;

}e[N<<];

bool cmp(Edge a,Edge b)

{

    return a.h < b.h;

}

struct Node

{

    int l,r;

    int s;

    double len;

}q[N*];

double x[*N];

void build(int i,int l,int r)

{

    q[i].l = l,q[i].r = r;

    q[i].s = ;q[i].len = ;

    if (l == r) return;

    int mid = m(i);

    build(ls,l,mid);

    build(rs,mid+,r);

}

void pushup(int i)

{

    if (q[i].s)

    {

        q[i].len = x[q[i].r+] - x[q[i].l];

    }

    else if (q[i].l == q[i].r)

    {

        q[i].len = ;

    }

    else

    {

        q[i].len = q[ls].len + q[rs].len;

    }

}

void update(int i,int l,int r,int xx)

{

    if (q[i].l == l&&q[i].r == r)

    {

        q[i].s += xx;

        pushup(i);

        return;

    }

    int mid = m(i);

    if (r <= mid) update(ls,l,r,xx);

    else if (l > mid) update(rs,l,r,xx);

    else

    {

        update(ls,l,mid,xx);

        update(rs,mid+,r,xx);

    }

    pushup(i);

}

int main()

{

    int n;int kas = ;

    while (scanf("%d",&n),n)

    {

        int tot = ;

        for (int i = ;i < n;++i)

        {

            double x1,x2,y1,y2;

            scanf("%lf %lf %lf %lf",&x1,&y1,&x2,&y2);

            Edge &t1 = e[tot];Edge &t2 = e[+tot];

            t1.l = t2.l = x1,t1.r = t2.r = x2;

            t1.h = y1;t1.f = ;

            t2.h = y2;t2.f = -;

            x[tot] = x1;x[tot+] = x2;

            tot += ;

        }

        sort(e,e+tot,cmp);

        sort(x,x+tot);

        int k = ;

        for (int i = ;i < tot;++i)

        {

            if (x[i] != x[i-])

            {

                x[k++] = x[i];

            }

        }

        build(,,k-);

        double ans = 0.0;

        for (int i = ;i < tot;++i)

        {

            int l = lower_bound(x,x+k,e[i].l) - x;

            int r = lower_bound(x,x+k,e[i].r) - x - ;

            update(,l,r,e[i].f);

            ans += (e[i+].h - e[i].h)*q[].len;

        }

        printf("%.0f\n",ans);

    }

    puts("*");

}

Minimum Distance in a Star Graph

问答

只看题面

41.93%
1000ms
262144K

In this problem, we will define a graph called star graph, and the question is to find the minimum distance between two given nodes in the star graph.

Given an integer nn, an n-dimensionaln−dimensionalstar graph, also referred to as S_{n}Sn, is an undirected graph consisting of n!n! nodes (or vertices) and ((n-1)\ *\ n!)/2((n−1) ∗ n!)/2 edges. Each node is uniquely assigned a label x_{1}\ x_{2}\ ...\ x_{n}x1 x2 ... xnwhich is any permutation of the n digits {1, 2, 3, ..., n}1,2,3,...,n. For instance, an S_{4}S4 has the following 24 nodes {1234, 1243, 1324, 1342, 1423, 1432, 2134, 2143, 2314, 2341, 2413, 2431, 3124, 3142, 3214, 3241, 3412, 3421, 4123, 4132, 4213, 4231, 4312, 4321}1234,1243,1324,1342,1423,1432,2134,2143,2314,2341,2413,2431,3124,3142,3214,3241,3412,3421,4123,4132,4213,4231,4312,4321. For each node with label x_{1}\ x_{2} x_{3}\ x_{4}\ ...\ x_{n}x1 x2x3 x4 ... xn, it has n-1n−1 edges connecting to nodes x_{2}\ x_{1}\ x_{3}\ x_{4}\ ...\ x_{n}x2 x1 x3 x4 ... xn, x_{3}\ x_{2}\ x_{1}\ x_{4}\ ...\ x_{n}x3 x2 x1 x4 ... xn, x_{4}\ x_{2}\ x_{3}\ x_{1}\ ...\ x_{n}x4 x2x_{n}\ x_{2}\ x_{3}\ x_{4}\ ...\ x_{1}n-1d-thx_{1}\ x_{2}\ x_{3}\ x_{4}\ ...\ x_{n}d = 2, ..., nS_{4}12343213432144231S_{4}abcd x3 x1 ... xn, ..., and xn x2 x3 x4 ... x1. That is, the n−1 adjacent nodes are obtained by swapping the first symbol and the d−th symbol of x1 x2 x3 x4 ... xn, for d=2,...,n. For instance, in S4, node 1234has 3 edges connecting to nodes 2134, 3214, and 4231. The following figure shows how S4looks (note that the symbols a, b, c, and d are not nodes; we only use them to show the connectivity between nodes; this is for the clarity of the figure).

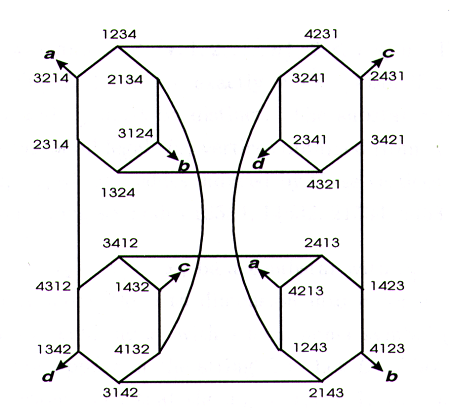
In this problem, you are given the following inputs:

nn: the dimension of the star graph. We assume that nn ranges from 44 to 99.
Two nodes x_{1}x1 x_{2}x2 x_{3}x3 ... x_{n}xn and y_{1}y1 y_{2}y2 y_{3}\ ...\ y_{n}y3 ... yn in S_{n}Sn.

You have to calculate the distance between these two nodes (which is an integer).

Input Format

nn (dimension of the star graph)

A list of 55 pairs of nodes.

Output Format

A list of 55 values, each representing the distance of a pair of nodes.

样例输入

样例输出

题目来源

2017 ACM-ICPC 亚洲区（南宁赛区）网络赛

这个题也很水，bfs一下就好，因为9！这个数并不大

#include<stdio.h>

#include<string.h>

#include<math.h>

#include<algorithm>

#include<map>

#include<queue>

#define LL long long

using namespace std;

struct mm

{

    int v,bu;

};

void bfs(int x,int y,int n)

{

    int b[],k=,i;

    map<int ,int>a;

    a[x]=;

    queue<mm>s;

    mm p;

    p.v=x;

    p.bu=;

    s.push(p);

    while(!s.empty()){

        mm q=s.front();s.pop();

        int now=q.v,bushu=q.bu;

        if(q.v==y){

            printf("%d\n",bushu);

            break;

        }

        k=n-;

        while(now){

            b[k--]=now%;

            now/=;

        }

        for(i=;i<n;i++){

            int sum=,j,t,tt;

            t=b[i];

            tt=b[];

            b[]=t;

            b[i]=tt;

            for(j=;j<n;j++){

                sum=sum*+b[j];

            }

            if(!a[sum]){

                a[sum]=;

                q.v=sum;

                q.bu=bushu+;

                s.push(q);

            }

            b[]=tt;

            b[i]=t;

        }

    }

}

int main()

{

    int n;

    scanf("%d",&n);

    int x,y;

    while(~scanf("%d%d",&x,&y)){

        bfs(x,y,n);

The Heaviest Non-decreasing Subsequence Problem

问答

只看题面

34.36%
1000ms
131072K

Let SS be a sequence of integers s_{1}s1, s_{2}s2, ......, s_{n}snEach integer is is associated with a weight by the following rules:

(1) If is is negative, then its weight is 00.

(2) If is is greater than or equal to 1000010000, then its weight is 55. Furthermore, the real integer value of s_{i}si is s_{i}-10000si−10000 . For example, if s_{i}siis 1010110101, then is is reset to 101101 and its weight is 55.

(3) Otherwise, its weight is 11.

A non-decreasing subsequence of SS is a subsequence s_{i1}si1, s_{i2}si2, ......, s_{ik}sik, with i_{1}<i_{2}\ ...\ <i_{k}i1<i2 ... <ik, such that, for all 1 \leq j<k1≤j<k, we have s_{ij}<s_{ij+1}sij<sij+1.

A heaviest non-decreasing subsequence of SSis a non-decreasing subsequence with the maximum sum of weights.

Write a program that reads a sequence of integers, and outputs the weight of its

heaviest non-decreasing subsequence. For example, given the following sequence:

8080 7575 7373 9393 7373 7373 1010110101 9797 -1−1 -1−1 114114 -1−11011310113 118118

The heaviest non-decreasing subsequence of the sequence is <73, 73, 73, 101, 113, 118><73,73,73,101,113,118> with the total weight being 1+1+1+5+5+1 = 141+1+1+5+5+1=14. Therefore, your program should output 1414 in this example.

We guarantee that the length of the sequence does not exceed 2*10^{5}2∗105

Input Format

A list of integers separated by blanks:s_{1}s1, s_{2}s2,......,s_{n}sn

Output Format

A positive integer that is the weight of the heaviest non-decreasing subsequence.

样例输入

80 75 73 93 73 73 10101 97 -1 -1 114 -1 10113 118

样例输出

题目来源

2017 ACM-ICPC 亚洲区（南宁赛区）网络赛

转换一下，求最长不降子序列就可以的

#include<iostream>

#include<algorithm>

#include<stdio.h>

using namespace std;

const int N=1e6+;

const int INF=0x3f3f3f3f;

int a[N],g[N],f[N],n;

int main() {

    int i=,j,k;

    while(scanf("%d",&a[i])!=EOF)

    {

        if(a[i]>=)

        {

            j=;

            k=a[i]-;

            while(j<)

            {

                a[i]=k;

                j++;

                i++;

            }

        }

        else if(a[i]>=)

        i++;

    }

        n=i;/*

    for(i=0;i<n;i++)printf("%d ",a[i]);*/

        fill(g,g+n,INF);

        for(int i=; i<n; i++) {

            int j=lower_bound(g, g+n,a[i])-g;

            while(g[j]==a[i])

            j++;

            g[j]=a[i];

        }

        printf("%d\n",lower_bound(g, g+n,INF)-g);

}

Frequent Subsets Problem

问答

只看题面

46.98%
1000ms
131072K

The frequent subset problem is defined as follows. Suppose UU={1, 2,\ldots…,N} is the universe, and S_{1}S1, S_{2}S2,\ldots…,S_{M}SM are MM sets over UU. Given a positive constant \alphaα, 0<\alpha \leq 10<α≤1, a subset BB (B \neq 0B≠0) is α-frequent if it is contained in at least \alpha MαM sets of S_{1}S1, S_{2}S2,\ldots…,S_{M}SM, i.e. \left | \left \{ i:B\subseteq S_{i} \right \} \right | \geq \alpha M∣{i:B⊆Si}∣≥αM. The frequent subset problem is to find all the subsets that are α-frequent. For example, let U=\{1, 2,3,4,5\}U={1,2,3,4,5}, M=3M=3, \alpha =0.5α=0.5, and S_{1}=\{1, 5\}S1={1,5}, S_{2}=\{1,2,5\}S2={1,2,5}, S_{3}=\{1,3,4\}S3={1,3,4}. Then there are 33 α-frequent subsets of UU, which are \{1\}{1},\{5\}{5} and \{1,5\}{1,5}.

Input Format

The first line contains two numbers NN and \alphaα, where NN is a positive integers, and \alphaα is a floating-point number between 0 and 1. Each of the subsequent lines contains a set which consists of a sequence of positive integers separated by blanks, i.e., line i + 1i+1 contains S_{i}Si, 1 \le i \le M1≤i≤M . Your program should be able to handle NN up to 2020 and MM up to 5050.

Output Format

The number of \alphaα-frequent subsets.

样例输入

15 0.4

1 8 14 4 13 2

3 7 11 6

10 8 4 2

9 3 12 7 15 2

8 3 2 4 5

样例输出

题目来源

2017 ACM-ICPC 亚洲区（南宁赛区）网络赛

#include<stdio.h>

#include<string.h>

#include<algorithm>

using namespace std;

int main()

{

    long long n,i,j,b[],l,x,m,y,s,h;

    double a,o;

    char c[];

    scanf("%lld%lf",&n,&a);

    j=;

    memset(b,,sizeof(b));

    getchar();

    while(gets(c)!=NULL)

    {

        l=strlen(c);

        i=;

        while(i<l)

        {

            if(c[i]>=''&&c[i]<='')

            {

                x=;

                while(i<l&&c[i]>=''&&c[i]<='')

                {

                    x=x*+c[i]-'';

                    i++;

                }

                b[j]|=(<<x);

            }

            i++;

        }

        j++;

    }

    m=j;s=;o=m*a;

    /*

for(i=0;i<m;i++)

    printf("%lld\n",b[i]);*/

    for(i=;i<(<<(n+));i++)

    {

        h=;

        x=i;

        for(j=;j<m;j++)

        {

            y=x&b[j];

            if(x==y)

            h++;

        }

        if(h>=o)

        s++;

    }

    printf("%lld\n",s);

}

A Cache Simulator

问答

只看题面

23.24%
1000ms
131072K

Cache memories have been used widely in current microprocessor systems. In this problem, you are asked to write a program for a cache simulator. The cache has the following metrics:

1. The cache size is 1 KB (K-byte).

2. The cache uses the direct mapped approach.

3. The cache line size is 16 bytes.

4. The cacheable memory size is 256MB.

Your program will report a hit or miss when an address is given to the cache simulator. This is often called trace simulation. Initially, all of the cache lines are in the invalid state. When a memory line is first brought into the cache, the allocated cache entry transits into the valid state. Assume that a miss causes the filling of a whole cache line.

Input Format

Up to 100100 lines of address can be given in the file. Each line consists of an address given to the simulator. The address is given in hexadecimal form. We assume that each address references only one byte of data. The input file ends at the line with the word ENDEND.

Output Format

Report either HitHit or MissMiss for each of the given addresses. The last line reports cache hit ratio in percentage, that is, the number of hits divided by the number of total addresses given.

样例输入

AAAA000

00010B2

00010BA

END

样例输出

Miss

Miss

Hit

Hit ratio = 33.33%

题目来源

2017 ACM-ICPC 亚洲区（南宁赛区）网络赛

这个H，毒瘤。。。cache

其实根据题目条件找到映射就可以了

#include<cstdio>

#include<cstring>

#include<cmath>

#include<iostream>

#include<algorithm>

using namespace std;

int a[];

int main()

{

    char s[];

    ios::sync_with_stdio(false);

    int m=,m0=;

    memset(a,-,sizeof(a));

    while(cin>>s)

    {

        if(strcmp(s,"END")==)break;

        m++;

        int n;

        sscanf(s,"%X",&n);

        int id=(n/)%,num=(n/)/;

        if(a[id]!=num)

        {

            a[id]=num;

            printf("Miss\n");

        }

        else

        {

            printf("Hit\n");

            m0++;

        }

    }

    printf("Hit ratio = %.2f%%\n",m0*100.0/m);

    return ;

}

Weather Patterns

问答

只看题面

76.25%
1000ms
131072K

Consider a system which is described at any time as being in one of a set of NN distinct states, 1,2,3,...,N1,2,3,...,N. We denote the time instants associated with state changes as t = 1,2,...t=1,2,..., and the actual state at time tt as a_{ij}=p=[s_{i}=j\ |\ s_{i-1}=i], 1\le i,j \le Naij=p=[si=j ∣ si−1=i],1≤i,j≤N. For the special case of a discrete, first order, Markovchain, the probabilistic description for the current state (at time tt) and the predecessor state is s_{t}st. Furthermore we only consider those processes being independent of time, thereby leading to the set of state transition probability a_{ij}aij of the form: with the properties a_{ij} \geq 0aij≥0 and \sum_{i=1}^{N} A_{ij} = 1∑i=1NAij=1. The stochastic process can be called an observable Markovmodel. Now, let us consider the problem of a simple 4-state Markov model of weather. We assume that once a day (e.g., at noon), the weather is observed as being one of the following:

State 11: snow

State 22: rain

State 33: cloudy

State 44: sunny

The matrix A of state transition probabilities is:

A = \{a_{ij}\}= \begin{Bmatrix} a_{11}&a_{12}&a_{13}&a_{14} \\ a_{21}&a_{22}&a_{23}&a_{24} \\ a_{31}&a_{32}&a_{33}&a_{34} \\ a_{41}&a_{42}&a_{43}&a_{44} \end{Bmatrix}A={aij}=⎩⎪⎪⎨⎪⎪⎧a11a21a31a41a12a22a32a42a13a23a33a43a14a24a34a44⎭⎪⎪⎬⎪⎪⎫

Given the model, several interestingquestions about weather patterns over time can be asked (and answered). We canask the question: what is the probability (according to the given model) thatthe weather for the next kdays willbe? Another interesting question we can ask: given that the model is in a knownstate, what is the expected number of consecutive days to stay in that state?Let us define the observation sequence OOas O = \left \{ s_{1}, s_{2}, s_{3}, ... , s_{k} \right \}O={s1,s2,s3,...,sk}, and the probability of the observation sequence OO given the model is defined as p(O|model)p(O∣model). Also, let the expected number of consecutive days to stayin state ii be E_{i}Ei. Assume that the initial state probabilities p[s_{1} = i] = 1, 1 \leq i \leq Np[s1=i]=1,1≤i≤N. Bothp(O|model)p(O∣model) and E_{i}Ei are real numbers.

Input Format

Line 11~44 for the state transition probabilities. Line 55 for the observation sequence O_{1}O1, and line 66 for the observation sequence O_{2}O2. Line 77and line 88 for the states of interest to find the expected number of consecutive days to stay in these states.

Line 11: a_{11}\ a_{12}\ a_{13}\ a_{14}a11 a12 a13 a14

Line 22: a_{21}\ a_{22}\ a_{23}\ a_{34}a21 a22 a23 a34

Line 33: a_{31}\ a_{32}\ a_{33}\ a_{34}a31 a32 a33 a34

Line 44: a_{41}\ a_{42}\ a_{43}\ a_{44}a41 a42 a43 a44

Line 55: s_{1}\ s_{2}\ s_{3}\ ...\ s_{k}s1 s2 s3 ... sk

Line 66: s_{1}\ s_{2}\ s_{3}\ ...\ s_{l}s1 s2 s3 ... sl

Line 77: ii

Line 88: jj

Output Format

Line 11 and line 22 are used to show the probabilities of the observation sequences O_{1}O1and O_{2}O2 respectively. Line 33 and line 44 are for the expected number of consecutive days to stay in states ii and jj respectively.

Line 11: p[O_{1} | model]p[O1∣model]

Line 22: p[O_{2} | model]p[O2∣model]

Line 33: E_{i}Ei

Line 44: E_{j}Ej

Please be reminded that the floating number should accurate to 10^{-8}10−8.

样例输入

0.4 0.3 0.2 0.1

0.3 0.3 0.3 0.1

0.1 0.1 0.6 0.2

0.1 0.2 0.2 0.5

4 4 3 2 2 1 1 3 3

2 1 1 1 3 3 4

3

4

样例输出

题目来源

2017 ACM-ICPC 亚洲区（南宁赛区）网络赛

这个是个题意题啊，看懂就出来了，我是读了n年的样例

#include<stdio.h>

#include<string.h>

int main()

{

    double a[][],s;

    int i,j,x,y,b[],l;

    char c[];

    for(i=;i<=;i++)

    {

        for(j=;j<=;j++)

        {

            scanf("%lf",&a[i][j]);

        }

    }

    getchar();

    gets(c);

    l=strlen(c);

    i=;j=;

    while(i<l)

    {

        if(c[i]>=''&&c[i]<='')

        {

            x=;

            while(i<l&&c[i]>=''&&c[i]<='')

            {

                x=x*+c[i]-'';

                i++;

            }

            b[j++]=x;

        }

        i++;

    }

    s=;

    for(i=;i<j;i++)

    {

        s*=a[b[i-]][b[i]];

    }

    printf("%.8lf\n",s);

    c[]=;

    //getchar();

    gets(c);

    l=strlen(c);

    i=;j=;

    while(i<l)

    {

        if(c[i]>=''&&c[i]<='')

        {

            x=;

            while(i<l&&c[i]>=''&&c[i]<='')

            {

                x=x*+c[i]-'';

                i++;

            }

            b[j++]=x;

        }

        i++;

    }

    s=;

    for(i=;i<j;i++)

    {

        s*=a[b[i-]][b[i]];

    }

    printf("%.8lf\n",s);

    scanf("%d",&x);

    printf("%.8lf\n",1.0/(-a[x][x]));

    scanf("%d",&x);

    printf("%.8lf\n",1.0/(-a[x][x]));

}

Auction Bidding

问答

只看题面

28.14%
1000ms
131072K

Company ABC is holding an antique auction. In the auction, there are NN, 1 \leq N \leq 10001≤N≤1000, lots. We number the lots from 11 to NN. There are MM, 1 \leq M \leq 5001≤M≤500, bidders participated in the auction. We number the bidders from 11to MM. The winning bid for each lot is determined by the following rules:

• Each lot has a reserved price, which is a positive integer.

• Each bidder may submit at most one bid to each lot whose amount must be a positive integer.

• A valid bid for a lot is one that is at least the reserved price for the lot. All invalid bids are not considered.

• The largest valid bid wins the lot and is called the winning bid. In case of tie bids, the bidder with the smaller bidder number wins. If there is no valid bid for a lot, then this lot is not sold.

• The second largest bid is a valid bid that does not win if one exists; otherwise, it is the reserved price.

• If a bidder wins a lot, then the final hammer price for this lot is either 10\%10% over the second largest bid or the largest valid bid, depending on which one is smaller. If the final hammer price is not an integer, then it is truncated to the nearest integer.

• Given the reserved price and the bids for each lot, your task is to decide the total final hammer prices for a given k, 0 < k \leq M0<k≤M, bidders.

Input Format

The input contains N + 3 + kN+3+k lines.

Line 11: NN

Line 22: MM

Line 33: r_{1}, b_{1,1}, p_{1,1}, b_{1,2}, p{1,2}, -1r1,b1,1,p1,1,b1,2,p1,2,−1

\ldots…

Line i + 2i+2: r_{i}, b_{i,1}, p_{i,1}, b_{i,2}, p{i,2}, -1ri,bi,1,pi,1,bi,2,pi,2,−1

\ldots…

Line N + 2N+2: r_{N}, b_{N,1}, p_{N,1}, b_{N,2}, p_{N,2}, -1rN,bN,1,pN,1,bN,2,pN,2,−1

Line N + 3N+3: kk

Line N + 4N+4: q_{1}q1

\ldots…

Line N + 3 + iN+3+i: q_{i}qi

\ldots…

Line N + 3 + kN+3+k: q_{k}qk

In Line i + 2i+2, r_{i}ri is the reserved price for lot ii. The number b_{i,j}bi,j and p{i,j}pi,j are the j^{th}jth bid for lot ii from bidder b_{i,j}bi,j with the amount p_{i,j}pi,j . Note that a space is between each number. The number -1−1 is added to mark the end of bids for a lot. In Line N+3N+3, kk is given. In line N + 3 + iN+3+i, you are asked to provide the total hammer prices for bidder q_{i}qi.

Output Format:

The output contains kk lines.

Line 11: h_{1}h1

\ldots…

Line ii: h_{i}hi

\ldots…

Line kk: h_{k}hk

The total hammer prices for bidder q_{i}qi is h_{i}hi.

Hint

In the sample, the bidder 11 got the the first lot 11at hammer price 1313.

样例输入

3

3

11 2 12 1 15 -1

5 3 4 -1

23 1 32 2 35 3 40 -1

1

1

样例输出

题目来源

2017 ACM-ICPC 亚洲区（南宁赛区）网络赛

这个C题意倒也好懂，主要还是精度问题

#include<iostream>

#include<stdio.h>

#include<algorithm>

#include<cstring>

#include<string>

#include<vector>

#define ll long long

#define INF 0x3f3f3f3f

#define N 200005

using namespace std;

vector<pair<int,int> > vec;

int n,m;

int low[N];

ll a[N];

int main()

{

    scanf("%d%d",&n,&m);

    {

        memset(a,,sizeof a);

        pair<int,int> pp;

        for(int i=;i<=n;i++)

        {

            vec.clear();

            scanf("%d",&low[i]);

            int x,f=;

            while(scanf("%d",&x),x!=-)

            {

                int d;

                scanf("%d",&d);

                if(d>=low[i])

                {

                    pp.first=-d;

                    pp.second=x;

                    vec.push_back(make_pair(-d,x));

                }

            }

            sort(vec.begin(),vec.end());

            if(vec.size()>=)

            {

                if(-vec[].first*1.1> -vec[].first) a[vec[].second]+= -vec[].first;

                else a[vec[].second]+=(int)(-vec[].first*1.1);

            }else if(vec.size()==){

                if(low[i]*1.1> -vec[].first) a[vec[].second]+= -vec[].first;

                else a[vec[].second]+=(int)(low[i]*1.1);

            }

        }

        int q;

        scanf("%d",&q);

        while(q--)

        {

            int s;

            scanf("%d",&s);

            printf("%lld\n",a[s]);

        }

    }

    return ;

}

Finding the Radius for an Inserted Circle

问答

只看题面

31.66%
1000ms
131072K

Three circles C_{a}Ca, C_{b}Cb, and C_{c}Cc, all with radius RRand tangent to each other, are located in two-dimensional space as shown in Figure 11. A smaller circle C_{1}C1 with radius R_{1}R1 (R_{1}<RR1<R) is then inserted into the blank area bounded by C_{a}Ca, C_{b}Cb, and C_{c}Cc so that C_{1}C1 is tangent to the three outer circles, C_{a}Ca, C_{b}Cb, and C_{c}Cc. Now, we keep inserting a number of smaller and smaller circles C_{k}\ (2 \leq k \leq N)Ck (2≤k≤N) with the corresponding radius R_{k}Rk into the blank area bounded by C_{a}Ca, C_{c}Cc and C_{k-1}Ck−1 (2 \leq k \leq N)(2≤k≤N), so that every time when the insertion occurs, the inserted circle C_{k}Ck is always tangent to the three outer circles C_{a}Ca, C_{c}Cc and C_{k-1}Ck−1, as shown in Figure 11

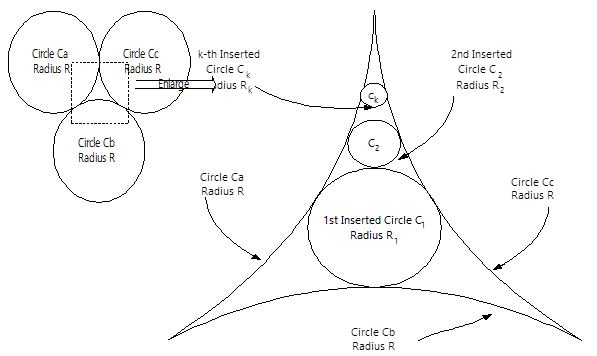
Figure 1.

(Left) Inserting a smaller circle C_{1}C1 into a blank area bounded by the circle C_{a}Ca, C_{b}Cb and C_{c}Cc.

(Right) An enlarged view of inserting a smaller and smaller circle C_{k}Ck into a blank area bounded by C_{a}Ca, C_{c}Cc and C_{k-1}Ck−1 (2 \leq k \leq N2≤k≤N), so that the inserted circle C_{k}Ck is always tangent to the three outer circles, C_{a}Ca, C_{c}Cc, and C_{k-1}Ck−1.

Now, given the parameters RR and kk, please write a program to calculate the value of R_{k}Rk, i.e., the radius of the k-thk−th inserted circle. Please note that since the value of R_kRk may not be an integer, you only need to report the integer part of R_{k}Rk. For example, if you find that R_{k}Rk = 1259.89981259.8998 for some kk, then the answer you should report is 12591259.

Another example, if R_{k}Rk = 39.102939.1029 for some kk, then the answer you should report is 3939.

Assume that the total number of the inserted circles is no more than 1010, i.e., N \leq 10N≤10. Furthermore, you may assume \pi = 3.14159π=3.14159. The range of each parameter is as below:

1 \leq k \leq N1≤k≤N, and 10^{4} \leq R \leq 10^{7}104≤R≤107.

Input Format

Contains l + 3l+3 lines.

Line 11: ll ----------------- the number of test cases, ll is an integer.

Line 22: RR ---------------- RR is a an integer followed by a decimal point,then followed by a digit.

Line 33: kk ---------------- test case #11, kk is an integer.

\ldots…

Line i+2i+2: kk ----------------- test case # ii.

\ldots…

Line l +2l+2: kk ------------ test case #ll.

Line l + 3l+3: -1−1 ---------- a constant -1−1representing the end of the input file.

Output Format

Contains ll lines.

Line 11: kk R_{k}Rk ----------------output for the value of kk and R_{k}Rk at the test case #11, each of which should be separated by a blank.

\ldots…

Line ii: kk R_{k}Rk ----------------output for kk and the value of R_{k}Rk at the test case # ii, each of which should be separated by a blank.

Line ll: kk R_{k}Rk ----------------output for kk and the value ofR_{k}Rk at the test case # ll, each of which should be separated by a blank.

样例输入

样例输出

1 23665

题目来源

2017 ACM-ICPC 亚洲区（南宁赛区）网络赛

笛卡尔定理搞一搞就行啊

#include<stdio.h>

#include<string.h>

#include<algorithm>

#include<math.h>

using namespace std;

int main()

{

    int n,i,j,u;

    double a,R,r,b[],co,p,x;

    while(scanf("%d",&n),n!=-)

    {

        scanf("%lf",&a);

        R=a,r=a;

        for(i=;i<=;i++)

        {

            co=(*(R+r)*(R+r)-(R+R)*(R+R))//(R+r)/(R+r);

            p=acos(co)/;

            co=cos(p);

            x=(*r-*R)-*(R+r)*co;

            x=(*(R+r)*co*r-*r*r-*R*r)/x;

            b[i]=x;

            r=x;

        }

        while(n--)

        {

            scanf("%d",&u);

            printf("%d %d\n",u,int(b[u]));

        }

    }

}

GSM Base Station Identification

问答

只看题面

52.07%
1000ms
131072K

In the Personal Communication Service systems such as GSM (Global System for Mobile Communications), there are typically a number of base stations spreading around the service area. The base stations are arranged in a cellular structure, as shown in the following figure. In each cell, the base station is located at the center of the cell.

For convenience, each cell is denoted by [ii, jj]. The cell covers the origin is denoted by [00, 00]. The cell in the east of [00, 00] is denoted by [11, 00]. The cell in the west of [00, 00] is denoted by [-1−1, 00]. The cell in the northeast of [00, 00] is denoted by [00, 11]. The cell in the southwest of [00, 00] is denoted by [00, -1−1]. This notation can be easily generalized, as shown in the above figure.

Now the question is as follows. We have a service area represented by a Euclidean plane (i.e., x-yx−y plane). Each unit is 11 Km. For example, point (55, 00) in the plane means the location at a distance of 55 Km to the east of the origin. We assume that there are totally 400400 cells, denoted by [ii, jj], i\ =\ -9 \ ... \ 10i = −9 ... 10, j\ =\ -9\ ... \ 10j = −9 ... 10. The base station of cell [00, 00] is located at the origin of the Euclidean plane. Each cell has a radius of RR = 55 Km, as shown in the following figure.

You are given an input (xx, yy), which indicates a mobile phone’s location. And you need to determine the cell [ii, jj] that covers this mobile phone and can serve this phone call.

For example, given a location (1010, 00), your program needs to output the cell [11, 00], which can cover this location. Specifically, the input and output are:

input = (xx, yy). hhis is a location on the Euclidean plane. This value will not exceed the service area covered by the 400400 cells. That is, you do not need to handle the exceptional case that the input is out of the boundary of the service area.
output = [ii, jj]. One of the 400400 cells that covers location [ii, jj]

Input Format

A list of 1010 locations.

Output Format

A list of 1010 cells covering the above 1010locations in the correct order.

Please be reminded that there exist a space between coordinates.

样例输入

样例输出

[0,0], [-1,2], [0,0], [1,1], [0,1], [0,2], [2,2], [-1,-1], [2,-1], [-1,0]

题目来源

2017 ACM-ICPC 亚洲区（南宁赛区）网络赛

这个I我并不懂，也不知道他们怎么过的，之后补一下吧

#include<bits/stdc++.h>

#define INF 0x3f3f3f3f

#define N 1005

using namespace std;

const double G = sqrt(3.0);

int xx[];

map<pair<int,int> , pair<int,int> > ans;

map<pair<int,int> ,bool> used;

void addd()

{

    xx[]=;

    xx[]=;

    for(int i=;i<=;i++)

    {

        xx[i]=xx[i-]+xx[i-];

    }

}

void check(int x,int y){

    int ii;

    int aa=;

    for(ii=;ii<;ii++) aa++;

    double a = *G/2.0*y+*G*x;

    double b = *1.5*y;

    int imin = a-;

    int imax = a+;

    int jmin = b-;

    int jmax = b+;

    for (int i=imin;i<=imax;i++){

        for (int j=jmin;j<=jmax;j++){

            bool flag = true;

            if (i>=a-*G/&&i<=a+*G/);else flag = false;

            if (!flag)continue;

            double top = G/*i+(b-G/*a)+;

            double bottom = G/*i+(b-G/*a)-;

            if (j>=bottom&&j<=top);else flag = false;

            if (!flag)continue;

            top = -G/*i+(b++G/*a);

            bottom = -G/*i+(b-+G/*a);

            if (j>=bottom&&j<=top);else flag = false;

            if (!flag)continue;

            if (!used[make_pair(i,j)]){

                ans[make_pair(i,j)] = make_pair(x,y);

                used[make_pair(i,j)] = true;

            }

        }

    }

}

int main(){

    for (int i=-;i<=;i++){

        for (int j=-;j<=;j++){

            check(i,j);

        }

    }

    int aa=;

    for(int ii=;ii<;ii++) aa++;

    for(int i=;i<=;i++)addd();

    int x,y;

    int T=;

    while (scanf("%d%d",&x,&y)!=EOF){

        T--;

        pair<int,int> res = ans[make_pair(x,y)];

        printf("[%d,%d]",res.first,res.second);

        if (T!=){

            printf(", ");

        }

    }

    printf("\n");

    return ;

}