UVA - 1416 Warfare And Logistics (最短路)
Description

The army of United Nations launched a new wave of air strikes on terroristforces. The objective of the mission is to reduce enemy's logistical mobility. Each airstrike will destroy a path and therefore increase the shipping cost of the shortest pathbetween
two enemy locations. The maximal damage is always desirable.
Let's assume that there are n enemy locations connected by
m bidirectional paths,each with specific shipping cost. Enemy's total shipping cost is given as
c = 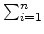
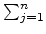 path(i,
path(i,
j). Here path(i, j) is the shortest path between locations
i and j. In case
i and j are not connected,
path(i, j) = L. Each air strike can only destroy one path. The total shipping cost after the strike is noted as
c'. In order to maximizedthe damage to the enemy, UN's air force try to find the maximal
c' - c.
Input
The first line ofeach input case consists ofthree integers:
n, m, and L.
1 < n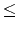 100,1
100,1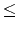 m
m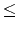 1000,
1000,
1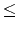 L
L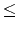 10
10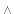 8.
8.
Each ofthe following m lines contains three integers:
a,b,
s, indicating length of the path between a and
b.
Output
For each case, output the total shipping cost before the air strike and the maximaltotal shipping cost after the strike. Output them in one line separated by a space.
Sample Input
4 6 1000
1 3 2
1 4 4
2 1 3
2 3 3
3 4 1
4 2 2
Sample Output
28 38
题意:给出一个n节点m条边的无向图,每条边上有一个正权,令c等于每对结点的最短路径之和,要求删除一条边后使得新的c值最大。不连通的两个点距离视为L
思路:每次求单源最短路的同一时候记录下删除边的值,然后计算最小值就是了
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <queue>
using namespace std;
typedef long long ll;
const int MAXN = 1010;
const int INF = 0x3f3f3f3f; struct Edge {
int from, to, dist;
}; struct HeapNode {
int d, u;
bool operator<(const HeapNode rhs) const {
return d > rhs.d;
}
}; struct Dijkstra {
int n, m;
vector<Edge> edges;
vector<int> G[MAXN];
bool done[MAXN];
ll d[MAXN];
int p[MAXN]; void init(int n) {
this->n = n;
for (int i = 0; i < n; i++)
G[i].clear();
edges.clear();
} void AddEdge(int from, int to, int dist) {
edges.push_back((Edge){from, to, dist});
edges.push_back((Edge){to, from, dist});
m = edges.size();
G[from].push_back(m-2);
G[to].push_back(m-1);
} void dijkstra(int s, int curEdge) {
priority_queue<HeapNode> Q;
for (int i = 0; i < n; i++)
d[i] = INF;
d[s] = 0;
memset(done, 0, sizeof(done));
memset(p, -1, sizeof(p));
Q.push((HeapNode){0, s});
while (!Q.empty()) {
HeapNode x = Q.top();
Q.pop();
int u = x.u;
if (done[u])
continue;
done[u] = true;
for (int i = 0; i < G[u].size(); i++) {
Edge &e = edges[G[u][i]];
if (G[u][i] == curEdge/2*2 || G[u][i] == curEdge/2*2+1)
continue;
if (d[e.to] > d[u] + e.dist) {
d[e.to] = d[u] + e.dist;
p[e.to] = G[u][i];
Q.push((HeapNode){d[e.to], e.to});
}
}
}
}
}arr; int pre[MAXN];
int n, m, L;
ll s[MAXN][MAXN], A[MAXN]; int main() {
while (scanf("%d%d%d", &n, &m, &L) != EOF) {
int u, v, w;
arr.init(n);
for (int i = 0; i < m; i++) {
scanf("%d%d%d", &u, &v, &w);
u--, v--;
arr.AddEdge(u, v, w);
}
ll ans = 0;
memset(s, -1, sizeof(s));
for (int i = 0; i < n; i++) {
arr.dijkstra(i, -100);
ll sum = 0;
for (int j = 0; j < n; j++) {
if (arr.d[j] == INF)
arr.d[j] = L;
sum += arr.d[j];
pre[j] = arr.p[j];
}
A[i] = sum;
ans += sum;
for (int j = 0; j < n; j++) {
if (j == i || pre[j] == -1)
continue;
ll tmp = 0;
arr.dijkstra(i, pre[j]);
for (int k = 0; k < n; k++) {
if (arr.d[k] == INF)
arr.d[k] = L;
tmp += arr.d[k];
}
s[pre[j]/2][i] = tmp;
}
}
ll Max = 0;
for (int i = 0; i < m; i++) {
ll sum = 0;
for (int j = 0; j < n; j++)
if (s[i][j] == -1)
sum += A[j];
else sum += s[i][j];
Max = max(Max, sum);
}
printf("%lld %lld\n", ans, Max);
}
return 0;
}
UVA - 1416 Warfare And Logistics (最短路)的更多相关文章
- uva 1416 Warfare And Logistics
题意: 给出一个无向图,定义这个无向图的花费是 其中path(i,j),是i到j的最短路. 去掉其中一条边之后,花费为c’,问c’ – c的最大值,输出c和c’. 思路: 枚举每条边,每次把这条边去掉 ...
- UVA 4080 Warfare And Logistics 战争与物流 (最短路树,变形)
题意: 给一个无向图,n个点,m条边,可不连通,可重边,可多余边.两个问题,第一问:求任意点对之间最短距离之和.第二问:必须删除一条边,再求第一问,使得结果变得更大. 思路: 其实都是在求最短路的过程 ...
- UVA1416 Warfare And Logistics
UVA1416 Warfare And Logistics 链接:http://acm.hust.edu.cn/vjudge/problem/viewProblem.action?id=36232 [ ...
- Warfare And Logistics UVA - 1416
题目链接:https://vjudge.net/problem/UVA-1416 题解: 这是一个最短路的好题,首先我们考虑如果暴力弗洛伊德,显然时间复杂度不对,如果做n次spfa好像复杂度也不对,所 ...
- 【UVA1416】(LA4080) Warfare And Logistics (单源最短路)
题目: Sample Input4 6 10001 3 21 4 42 1 32 3 33 4 14 2 2Sample Output28 38 题意: 给出n个节点m条无向边的图,每条边权都为正.令 ...
- UVA 11374 Airport Express(最短路)
最短路. 把题目抽象一下:已知一张图,边上的权值表示长度.现在又有一些边,只能从其中选一条加入原图,使起点->终点的距离最小. 当加上一条边a->b,如果这条边更新了最短路,那么起点st- ...
- UVALive 4080 Warfare And Logistics (最短路树)
很多的边会被删掉,需要排除一些干扰进行优化. 和UVA - 1279 Asteroid Rangers类似,本题最关键的地方在于,对于一个单源的最短路径来说,如果最短路树上的边没有改变的话,那么最短路 ...
- UVa 1599 (字典序最小的最短路) Ideal Path
题意: 给出一个图(图中可能含平行边,可能含环),每条边有一个颜色标号.在从节点1到节点n的最短路的前提下,找到一条字典序最小的路径. 分析: 首先从节点n到节点1倒着BFS一次,算出每个节点到节点n ...
- LA4080/UVa1416 Warfare And Logistics 最短路树
题目大意: 求图中两两点对最短距离之和 允许你删除一条边,让你最大化删除这个边之后的图中两两点对最短距离之和. 暴力:每次枚举删除哪条边,以每个点为源点做一次最短路,复杂度\(O(NM^2logN)\ ...
随机推荐
- [python篇] [伯乐在线][1]永远别写for循环
首先,让我们退一步看看在写一个for循环背后的直觉是什么: 1.遍历一个序列提取出一些信息 2.从当前的序列中生成另外的序列 3.写for循环已经是我的第二天性了,因为我是一个程序员 幸运的是,Pyt ...
- linux下文件显示被加锁如何解决?
1.很多时候从别的机器上拷贝过来的文件,没有权限打开,上面有一个小锁. 2.判断是权限没有,查询ls -al得知文件的的所有者,和所有者在的组都不是本机 3.使用chown改变用户的所有者和所有者所在 ...
- 安装anaconda并配置环境
安装anaconda的步骤 1.确定系统信息 uname -a 2.下载对应版本 3.sh 安装shell脚本 4.添加到对应路径 5.安装完anaconda之后,创建虚拟环境 conda creat ...
- 用echarts.js制作中国地图,点击对应的省市链接到指定页面
这里使用的是ECharts 2,因为用EChart 3制作的地图上的省市文字标识会有重叠,推测是引入的地图文件china.js,绘制文字的坐标方面的问题,所以,这里还是使用老版本. ECharts 2 ...
- Codeforces 891 C Envy
题目大意 给定一个 $n$ 个点 $m$ 条边的连通的无向图,每条边有一个权值,可能有重边.给出 $q$ 组询问,一组询问给出 $k$ 条边,问是否存在一棵最小生成树包含这 $k$ 条边. 思路 这道 ...
- HDU——1058Humble Numbers(找规律)
Humble Numbers Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others) T ...
- 【BZOJ1103】大都市meg(DFS序,树状数组)
题意:有一颗树,1号点为根,保证编号小的点深度较小,初始状态每条边都没有被标记,要求实现两个操作在线: A:将连接x,y的边标记 W:查询从1到x的路径上有多少条边未被标记 n<=2*10^5 ...
- error C2253: pure specifier or abstract override specifier only allowed on virtual
1.用Visual Studio 2012编译下面代码时出现的错误: #define RTC_DISALLOW_COPY_AND_ASSIGN(TypeName) \ TypeName(const T ...
- 用python生成二维码
Python生成二维码,可以使用qrcode模块, github地址 我是搬运工 首先安装, 因为打算生成好再展示出来,所以用到Pillow模块 pip install qrcode pip inst ...
- Scrapy学习-14-验证码识别
3种实现方案 1. 编码实现 tesseract-ocr 谷歌开源的识别工具,自己实现代码编码,投入精力大,回馈低.且平台验证码更换周期短,编好的代码容易失效 2. 在线打码 在线平台提供,识别率 ...
