UVA10294 Arif in Dhaka (First Love Part 2) —— 置换、poyla定理
题目链接:https://vjudge.net/problem/UVA-10294


题解:
白书P146~147。
为什么旋转i个间距,就有gcd(i,n)个循环,且每个循环有n/gcd(i,n)个元素?
证明:
(gcd:最大公约数,lcm:最小公倍数)
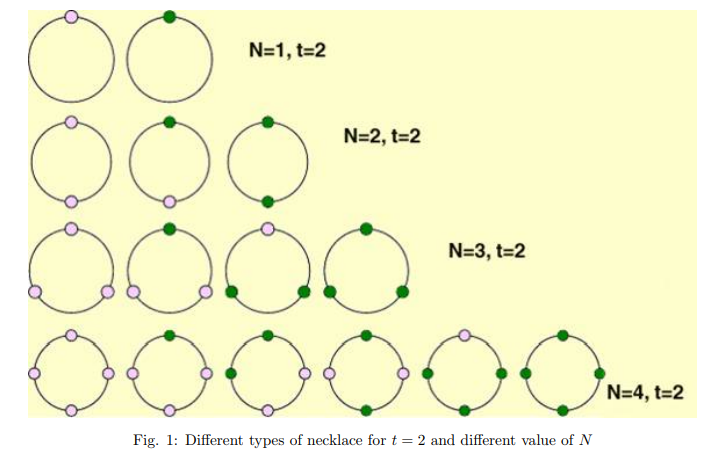
将珠子从0到n-1标号,对于旋转i位的置换,在以0号为起点,长度为t的一个循环节中,元素标号为:0,i%n,(i*2)%n,…,(i*(t-1))%n
易知:(i*t)%n==0(循环大小为t,跳t次就回到初始点0),即 n*k == i*t,其中n,k,i,t为正整数,因此等式左右的最小值为lcm(n,i),即i*t==lcm(n,i),为什么i*t取最小值,即t取最小值?因为是从0第一次跳到0就完成整个循环的遍历,这个“第一次”就决定了是最早满足条件的那个t,即最小t。
∴ t == lcm(n,i)/i == ( n*i/gcd(n,i) )/i == n/gcd(n,i)
∴ 循环节t==n/gcd(n,i),循环节的个数为:n/t == gcd(n,i)
代码如下:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <string>
#include <set>
using namespace std;
typedef long long LL;
const int INF = 2e9;
const LL LNF = 9e18;
const int MOD = 1e9+;
const int MAXN = ; LL gcd(LL a, LL b)
{
return b==?a:gcd(b,a%b);
} LL Pow[MAXN];
int main()
{
int n, t;
while(scanf("%d%d", &n,&t)!=EOF)
{
Pow[] = ;
for(int i = ; i<=n; i++) Pow[i] = 1LL*Pow[i-]*t;
LL a = , b = ;
for(int i = ; i<n; i++)
a += Pow[gcd(i,n)];
if(n%)
b = 1LL*n*Pow[n/+];
else
b = 1LL*n/*(Pow[n/]+Pow[n/+]); printf("%lld %lld\n", a/n, (a+b)//n);
}
}
UVA10294 Arif in Dhaka (First Love Part 2) —— 置换、poyla定理的更多相关文章
- [Uva10294]Arif in Dhaka
[Uva10294]Arif in Dhaka 标签: 置换 Burnside引理 题目链接 题意 有很多个珠子穿成环形首饰,手镯可以翻转和旋转,项链只能旋转.(翻转过的手镯相同,而项链不同) 有n个 ...
- UVA10294 Arif in Dhaka (群论,Polya定理)
UVA10294 Arif in Dhaka (群论,Polya定理) 题意 : 给你一个长为\(n\)的项链和手镯,每个珠子有\(m\)种颜色. 两个手镯定义为相同,即它们通过翻转和旋转得到一样的手 ...
- UVA10294 Arif in Dhaka (First Love Part 2)
题意 PDF 分析 用n颗宝石串成项链和手镯, 每颗宝石的颜色可以t种颜色中的一种,当A类项链经过旋转得B类项链时,A和B属于一类项链, 而手镯不仅可以旋转还可以翻转,当A类手镯经过翻转得得到B类手镯 ...
- Uva10294 Arif in Dhaka (置换问题)
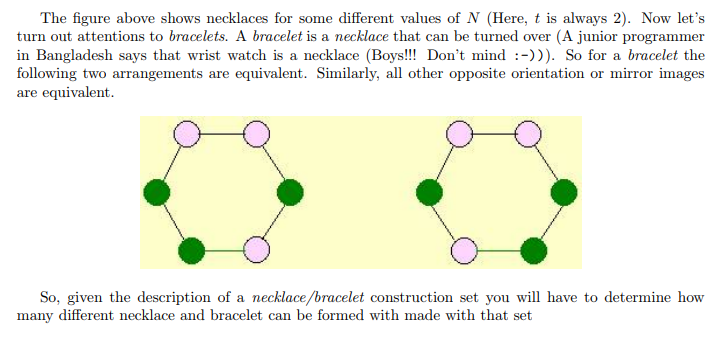
扯回正题,此题需要知道的是置换群的概念,这点在刘汝佳的书中写的比较详细,此处不多做赘述.此处多说一句的是第二种手镯的情况.在下图中“左图顺时针转1个位置”和“右图顺时针旋转5个位置”是相同的,所以在最 ...
- 【uva 10294】 Arif in Dhaka (First Love Part 2) (置换,burnside引理|polya定理)
题目来源:UVa 10294 Arif in Dhaka (First Love Part 2) 题意:n颗珠子t种颜色 求有多少种项链和手镯 项链不可以翻转 手镯可以翻转 [分析] 要开始学置换了. ...
- UVa 10294 (Pólya计数) Arif in Dhaka (First Love Part 2)
Burnside定理:若一个着色方案s经过置换f后不变,称s为f的不动点,将置换f的不动点的数目记作C(f).等价类的数目等于所有C(f)的平均值. 一个项链,一个手镯,区别在于一个能翻转一个不能,用 ...
- Uva 10294 Arif in Dhaka (First Love Part 2)
Description 现有一颗含\(N\)个珠子的项链,每个珠子有\(t\)种不同的染色.现求在旋转置换下有多少种本质不同的项链,在旋转和翻转置换下有多少种本质不同的项链.\(N < 51,t ...
- UVa 10294 Arif in Dhaka (First Love Part 2)(置换)
题目链接:http://acm.hust.edu.cn/vjudge/problem/viewProblem.action?id=35397 [思路] Polya定理. 旋转:循环节为gcd(i,n) ...
- Arif in Dhaka (First Love Part 2) UVA - 10294(Polya定理)
这题和POJ-1286一样 题意: 给出t种颜色的n颗珠子 (每种颜色的珠子个数无限制,但总数必须是n), 求能制作出项链和手镯的个数 注意手镯可以翻转和旋转 而 项练只能旋转 解析: 注意Poly ...
随机推荐
- 【2048小游戏】——CSS/原生js爬坑之纯CSS模态对话框&游戏结束
引言:2048小游戏的结束界面,使用纯CSS制作模态对话框,一般做模态对话框都会使用BootStrap自带的模态对话框组件方便使用,但在制作要运行在移动端的小项目时,就不能使用BootStrap,因为 ...
- IT行业是吃青春饭的吗?
作者:杨中科 1.“it专业的学生太多了,而且就业压力很大”是吗? 现在各个大学为了赚钱拼命扩招,所以不仅IT专业的学生人比较多,而且其他专业的学生人数也比较多,“僧多粥少”就通常意味着就业压 ...
- VueJS条件语句:v-if、v-else、v-else-if
HTML:if-else <!DOCTYPE html> <html> <head> <meta charset="utf-8"> ...
- 2个YUV视频拼接技术
http://blog.csdn.net/huahuahailang/article/details/9040847 2个YUV视频拼接技术 http://zhongcong386.blog.163. ...
- Bootstrap学习速查表(二) 排版及表格
一.h1~h6标签 固定不同级别标题字体大小,h1=36px,h2=30px,h3=24px,h4=18px,h5=14px和h6=12px. 1.重新设置了margin-top和margin-bot ...
- java 动态实现接口
package com.yhouse.modules.daos; public interface IUserDao { public String getUserName(); public Str ...
- 自制小工具大大加速MySQL SQL语句优化(附源码)
引言 优化SQL,是DBA常见的工作之一.如何高效.快速地优化一条语句,是每个DBA经常要面对的一个问题.在日常的优化工作中,我发现有很多操作是在优化过程中必不可少的步骤.然而这些步骤重复性的执行,又 ...
- hdu 5071 Chat-----2014acm亚洲区域赛鞍山 B题
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=5071 Chat Time Limit: 2000/1000 MS (Java/Others) M ...
- KVM+VNC 虚拟机远程管理
1.安装kvm grep -E -o 'vmx|svm' /proc/cpuinfo #检查服务器是否支持虚拟化(vmx为interl平台.svm是AMD平台) #安装KVM所需软件包: yum gr ...
- chessy 提高篇系列 阅读笔记
java提高篇(一)—–理解java的三大特性之封装 封装的好处, 汇聚属性和方法 减少修改对 其他处的影响 控制get和set方法. java提高篇(二)—–理解java的三大特性之继承 继承的好处 ...
