python 常用算法

算法就是为了解决某一个问题而采取的具体有效的操作步骤

算法的复杂度，表示代码的运行效率，用一个大写的O加括号来表示，比如O(1)，O(n)

认为算法的复杂度是渐进的，即对于一个大小为n的输入，如果他的运算时间为n³+5n+9，那么他的渐进时间复杂度是n³

递归

递归就是在函数中调用本身，大多数情况下，这会给计算机增加压力，但是有时又很有用，比如下面的例子：

汉诺塔游戏

把A柱的盘子，移动到C柱上，最少需要移动几次，大盘子只能在小盘子下面

递归实现：

def hanoi(x, a, b, c):  # 所有的盘子从 a 移到 c

    if x > 0:
        hanoi(x-1, a, c, b)  # step1：除了下面最大的，剩余的盘子 从 a 移到 b
        print('%s->%s' % (a, c))  # step2:最大的盘子从 a 移到 c
        hanoi(x-1, b, a, c)  # step3: 把剩余的盘子 从 b 移到 c

hanoi(10, 'A', 'B', 'C')

#计算次数

def h(x):
    num = 1
    for i in range(x-1):
        num = 2*num +1

    print(num)
h(10)

用递归打印斐波那契数列

def fei(n):
    if n == 0:
        return 0
    elif n == 1:
        return 1
    else:
        return fei(n-1)+fei(n-2)

你会发现，即使n只有几十的时候，你的计算机内存使用量已经飙升了

其实，如果结合生成器，你会发现不管n有多大，都不会出现卡顿，但这是生成器的特性，本篇博客不重点介绍

# 结合生成器
def fei(n):
    pre,cur = 0,1
    while n >=0:
        yield pre
        n -= 1
        pre,cur = cur,pre+cur

for i in fei(400000):
    print(i)

关于递归次数，Python中有个限制，可以通过sys模块来修改

import sys
sys.setrecursionlimit(1000000)

---

查找

1.顺序查找

这个没的说，就是for循环呗，时间复杂度O(n)

def linear_search(data_set, value):
    for i in range(len(data_set)):
        if data_set[i] == value:
            return i
    return

2.二分查找

时间复杂度O(logn)

就是一半一半的查找，看目标值在左边一半还是右边一半，然后替换左端点或者右端点，继续判断

非递归版本：

def binary_serach(li,val):
    low = 0
    high = len(li)-1
    while low <= high:
        mid = (low+high)//2
        if li[mid] == val:
            return mid
        elif li[mid] > val:
            high = mid-1
        else:
            low = mid+1
    else:
        return None

递归版本的二分查找

def bin_search_rec(data_set, value, low, high):
    if low < high:
        mid = (low + high) // 2
        if data_set[mid] == value:
            return mid
        elif data_set[mid] > value:
            return bin_search_rec(data_set, value, low, mid - 1)
        else:
            return bin_search_rec(data_set, value, mid + 1, high)
    else:
        return None

---

排序

速度慢的三个：

1.冒泡排序

　　原理就是，列表相邻的两个数，如果前边的比后边的小，那么交换顺序，经过一次排序后，最大的数就到了列表最前面

　　代码：　　

def bubble_sort(li):

    for j in range(len(li)-1):
        for i in range(1, len(li)):
            if li[i] > li[i-1]:
                li[i], li[i-1] = li[i-1], li[i]

    return li

冒泡排序的最差情况，即每次都交互顺序的情况，时间复杂度是O(n²)

存在一个最好情况就是列表本来就是排好序的，所以可以加一个优化，加一个标志位，如果没有出现交换顺序的情况，那就直接return

# 优化版本的冒泡
def bubble_sort_opt(li):
    for j in range(len(li)-1):
        flag = False
        for i in range(1, len(li)):
            if li[i] > li[i-1]:
                li[i], li[i-1] = li[i-1], li[i]
                flag = True
        if not flag:
            return li
    return li

2.插入排序

　　原理：把列表分为有序区和无序区两个部分。最初有序区只有一个元素。然后每次从无序区选择一个元素，插入到有序区的位置，直到无序区变空。

def insert_sort(li):
    for i in range(1,len(li)):
        tmp = li[i]
        j = i - 1
        while j >= 0 and tmp < li[j]:　　　　# 找到一个合适的位置插进去
            li[j+1] = li[j]
            j -= 1
        li[j+1] = tmp
    return li

　　简单形象的一张图：

时间复杂度是O(n²)

　　示例如下：

def insert_sort(li):
    '''
    初始时手里（有序区）只有一张牌
    每次（从无序区）摸一张牌，插入到手里已有牌的正确位置
    :param li:
    :return:
    '''
    for i in range(1, len(li)):
        tmp = li[i]
        j = i - 1
        while j >= 0 and tmp < li[j]:
            li[j+1] = li[j]
            j = j - 1
        li[j+1] = tmp
        print(li)
    return li
li = [6,5,4,3,2,1]
print('li:   ', li)
res = insert_sort(li)
print('res:   ', res)

'''
li:    [6, 5, 4, 3, 2, 1]
[5, 6, 4, 3, 2, 1]
[4, 5, 6, 3, 2, 1]
[3, 4, 5, 6, 2, 1]
[2, 3, 4, 5, 6, 1]
[1, 2, 3, 4, 5, 6]
res:    [1, 2, 3, 4, 5, 6]
'''

　　

3.选择排序

　　原理：遍历列表一遍，拿到最小的值放到列表第一个位置，再找到剩余列表中最小的值，放到第二个位置。。。。

def select_sort(li):
    for i in range(len(li)-1):
        min_loc = i         # 假设当前最小的值的索引就是i
        for j in range(i+1,len(li)):
            if li[j] < li[min_loc]:
                min_loc = j
        if min_loc != i:   # min_loc 值如果发生过交换，表示最小的值的下标不是i,而是min_loc
            li[i],li[min_loc] = li[min_loc],li[i]

    return li

时间复杂度是O(n²)

速度快的几种排序：

4.快速排序（快排）

原理：让指定的元素归位，所谓归位，就是放到他应该放的位置（左变的元素比他小，右边的元素比他大），然后对每个元素归位，就完成了排序

可以参考这个动图来理解下面的代码

代码：

#  归位函数
def partition(data, left, right): # 左右分别指向两端的元素
    tmp = data[left]                # 把左边第一个元素赋值给tmp,此时left指向空
    while left < right:             # 左右两个指针不重合，就继续
        while left < right and data[right] >= tmp:  # right指向的元素大于tmp,则不交换
            right -= 1                      # right 向左移动一位
        data[left] = data[right]            # 如果right指向的元素小于tmp，就放到左边现在为空的位置
        while left < right and data[left] <= tmp:   # 如果left指向的元素小于tmp,则不交换
            left += 1                       # left向右移动一位
        data[right] = data[left]            # 如果left指向的元素大于tmp,就交换到右边
    data[left] = tmp            # 最后把最开始拿出来的那个值，放到左右重合的那个位置
    return left                 # 最后返回这个位置

#  写好归位函数后，就可以递归调用这个函数，实现排序
def quick_sort(data, left, right):
    if left < right:
        mid = partition(data, left, right)  # 找到指定元素的位置
        quick_sort(data, left, mid - 1)     # 对左边元素排序
        quick_sort(data, mid + 1, right)    # 对右边元素排序
    return data

正常的情况，快排的复杂度是O(nlogn)

快排存在一个最坏情况，就是每次归位，都不能把列表分成两部分，此时复杂度就是O(n²)了，如果要避免设计成这种最坏情况，可以在取第一个数的时候不要取第一个了，而是取一个列表中的随机数

5.归并排序

原理：列表分成两段有序，然后分解成每个元素后，再合并成一个有序列表，这种操作就叫做一次归并

　　应用到排序就是，把列表分成一个元素一个元素的，一个元素当然是有序的，将有序列表一个一个合并，最终合并成一个有序的列表

　　

图示：

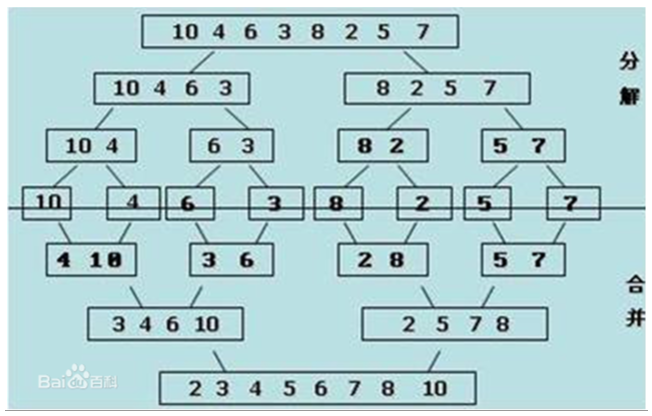
代码：

def merge(li, left, mid, right):
    # 一次归并过程，把从mid分开的两个有序列表合并成一个有序列表
    i = left
    j = mid + 1
    ltmp = []
    # 两个列表的元素依次比较，按从大到小的顺序放到一个临时的空列表中
    while i <= mid and j <= right:
        if li[i] < li[j]:
            ltmp.append(li[i])
            i += 1
        else:
            ltmp.append(li[j])
            j += 1

    # 如果两个列表并不是平均分的，就会存在有元素没有加入到临时列表的情况，所以再判断一下
    while i<= mid:
        ltmp.append(li[i])
        i += 1
    while j <= right:
        ltmp.append(li[j])
        j += 1
    li[left:right+1] = ltmp
    return li

def _merge_sort(li, left, right):
    # 细分到一个列表中只有一个元素的情况，对每一次都调用merge函数变成有序的列表
    if left < right:
        mid = (left+right)//2
        _merge_sort(li, left, mid)
        _merge_sort(li, mid+1, right)
        merge(li, left, mid, right)
    return li

def merge_sort(li):
    return(_merge_sort(li, 0, len(li)-1))

照例，时间复杂度是O(nlogn)

特殊的，归并排序还有一个O(n)的空间复杂度

6.堆排序

把这个放到最后，是因为这个是最麻烦的，把最麻烦的放到最后，是一种对工作负责的表现

如果要说堆排序，首先得先把‘树’搞明白

树

树是一种数据结构；

树是由n个节点组成的集合； -->如果n为0，那这是一颗空树，如果n>0，那么那存在1个节点作为树的根节点，其他节点可以分为m个集合，每个集合本身又是一棵树。

一些可能会用到的概念：

　　根节点：树的第一个节点，没有父节点的节点

　　叶子节点：不带分叉的节点

　　树的深度（高度）：就是分了多少层

　　孩子节点、父节点：节点与节点之间的关系

图示：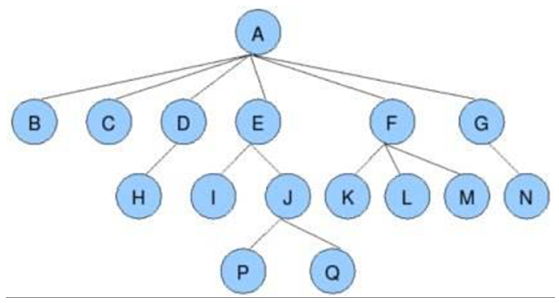

二叉树

然后在树的基础上，有一个二叉树，二叉树就是每个节点最多有两个子节点的树结构，比如这个：

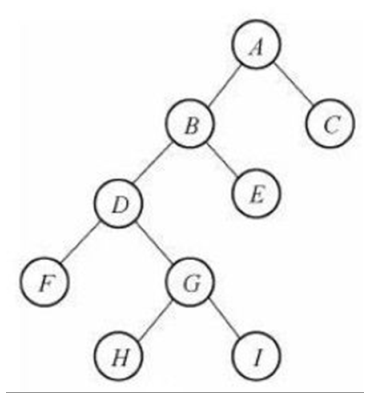
满二叉树：除了叶子节点，所有节点都有两个孩子，并且所有叶子节点深度都一样

完全二叉树：是有满二叉树引申而来，假设二叉树深度为k，那么除了第k层，之前的每一层的节点数都达到最大，即没有空的位置，而且第k层的子节点也都集中在左子树上（顺序）

二叉树的存储方式

有链式存储和顺序存储的方式（列表），本篇只讨论顺序存储的方式

思考：

　　父节点和左孩子节点的编号下标有什么关系？　　　　0-1 1-3 2-5 3-7 4-9         i  ---->   2i+1

　　父节点和右孩子节点的编号下标有什么关系？　　　　0-2 1-4 2-6 3-8 4-10　　i  ----->  2i+2

再来了解下堆，堆说起来又麻烦了，我将在另一篇博客中单独写堆，栈等这些数据结构，本篇先讨论与排序有关的东西

堆

堆是一类特殊的树，要求父节点大于或小于所有的子节点

大根堆：一棵完全二叉树，满足任一节点都比其孩子节点大  　　，升序用大根堆

小根堆：一棵完全二叉树，满足任一节点都比其孩子节点小

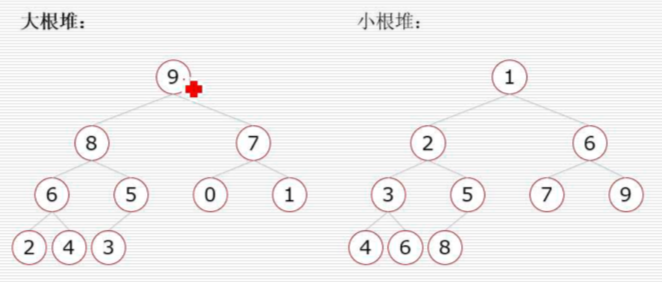
堆的调整：当根节点的左右子树都是堆时，可以通过一次向下的调整来将其变换成一个堆。

所谓一次向下调整，就是说把堆顶的值，向下找一个合适的位置，是一次一次的找，跟他交换位置的值，也要找到一个合适的位置

　　　　“浏览器写的没保存，丢失了，所以这块不想再写了。。。”

堆排序的过程

　　1.构造堆

　　2.得到堆顶元素，就是最大的元素

　　3.去掉堆顶，将堆的最后一个元素放到堆顶，此时可以通过一次调整重新使堆有序

　　4.堆顶元素为第二大元素

　　5.重复步骤3，直到堆为空

其中构造堆的过程：

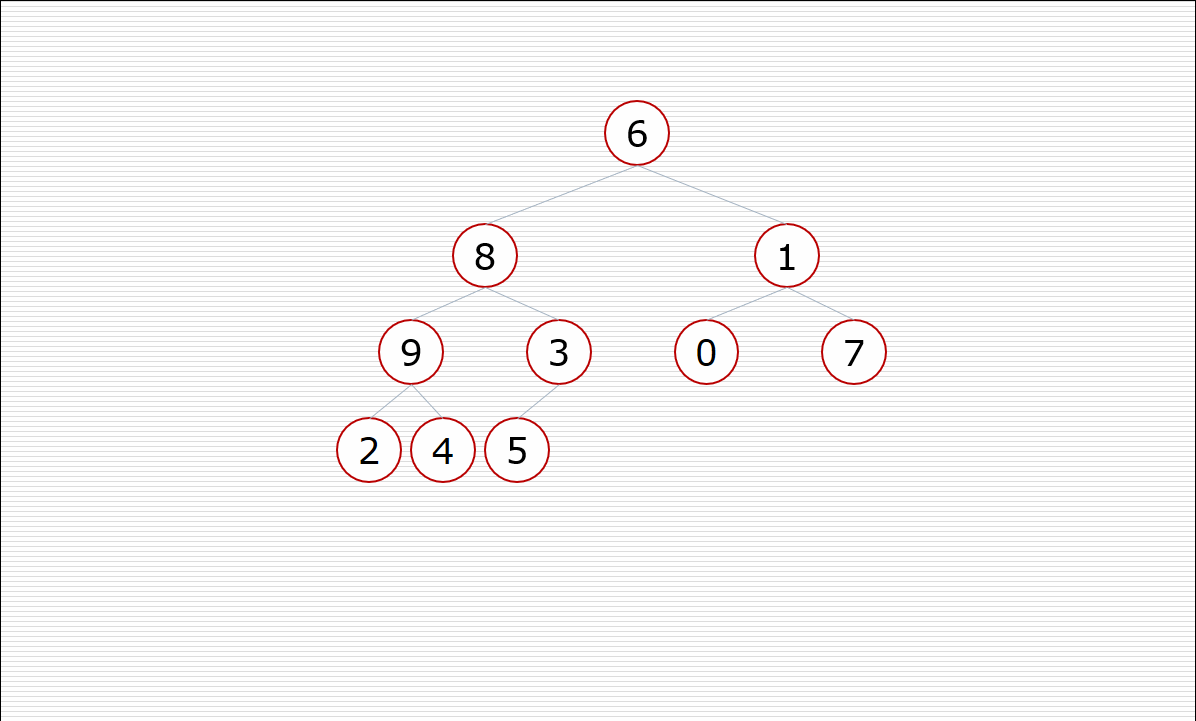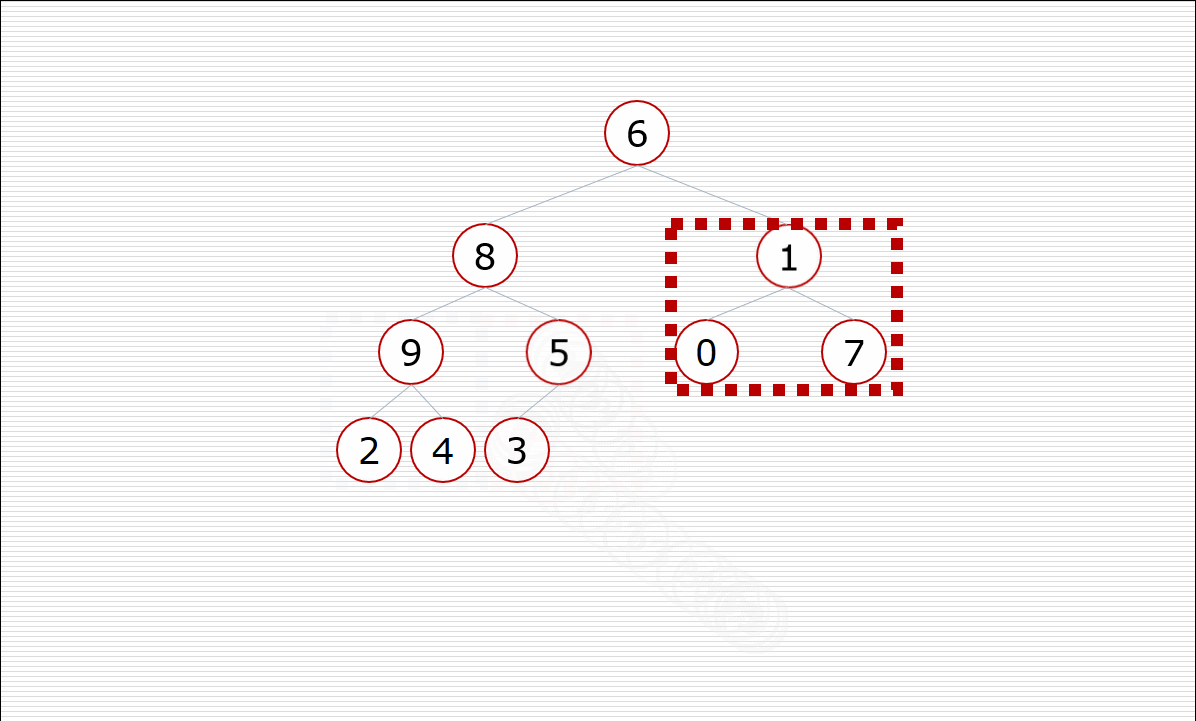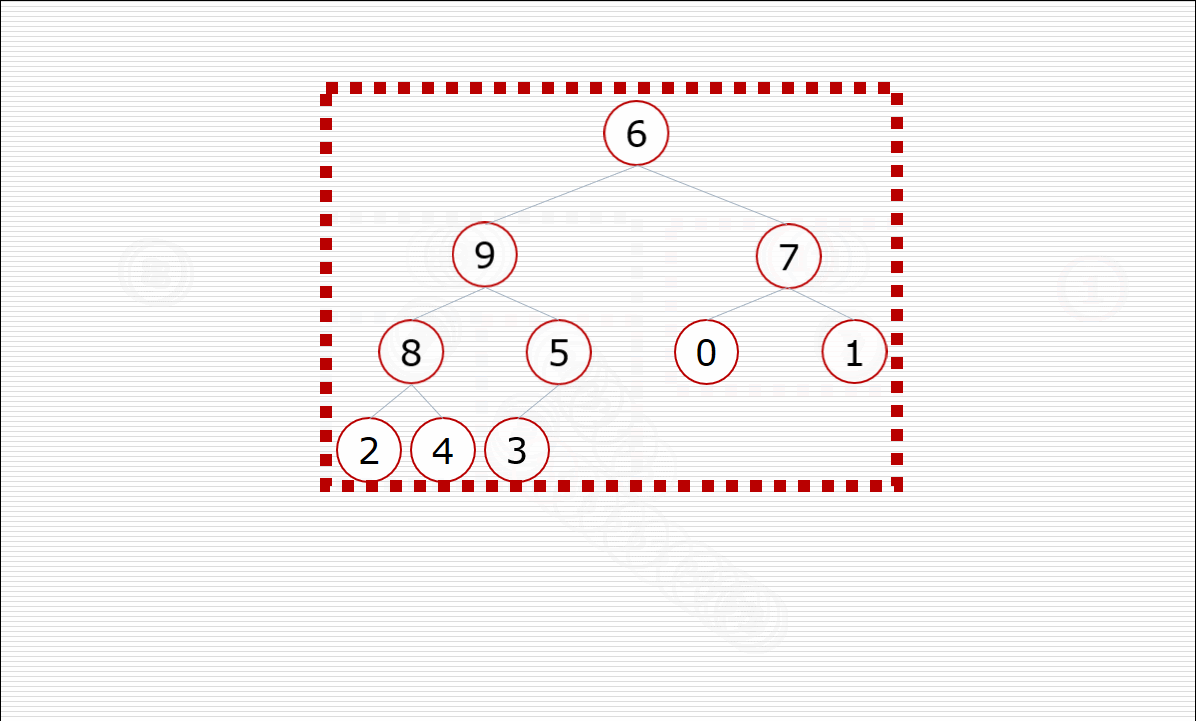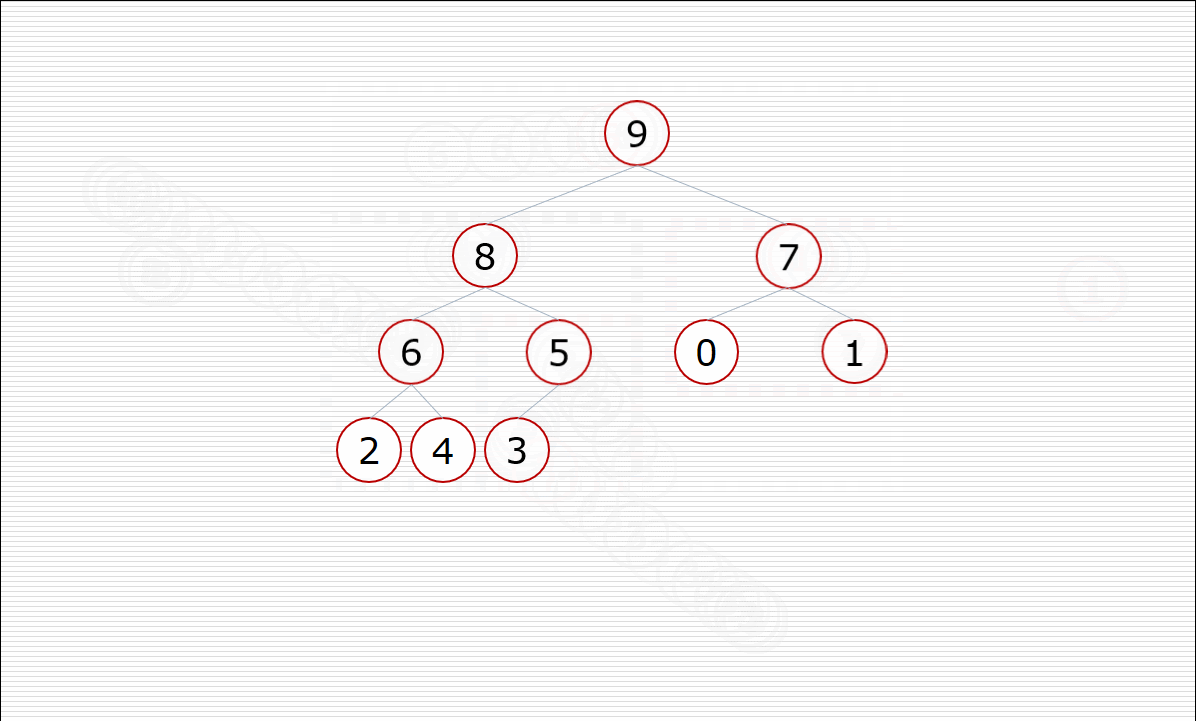
挨个出数的过程：

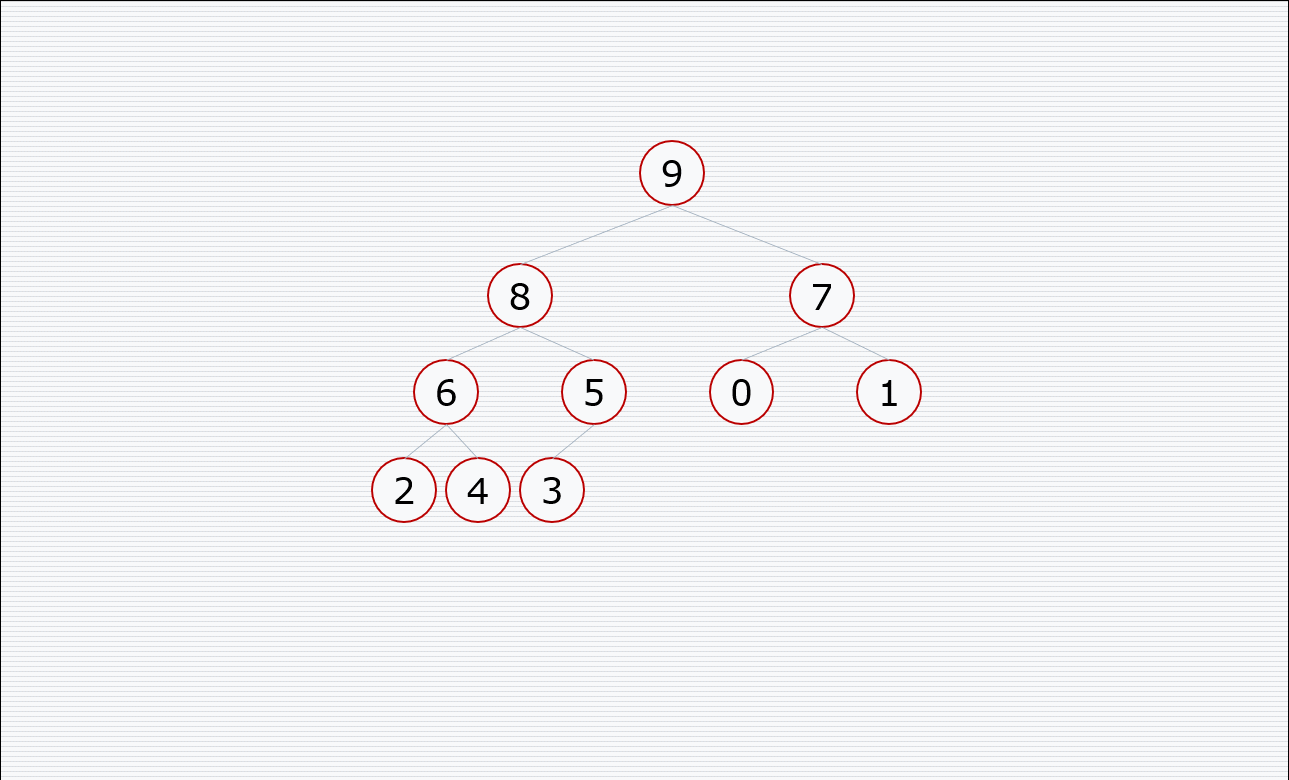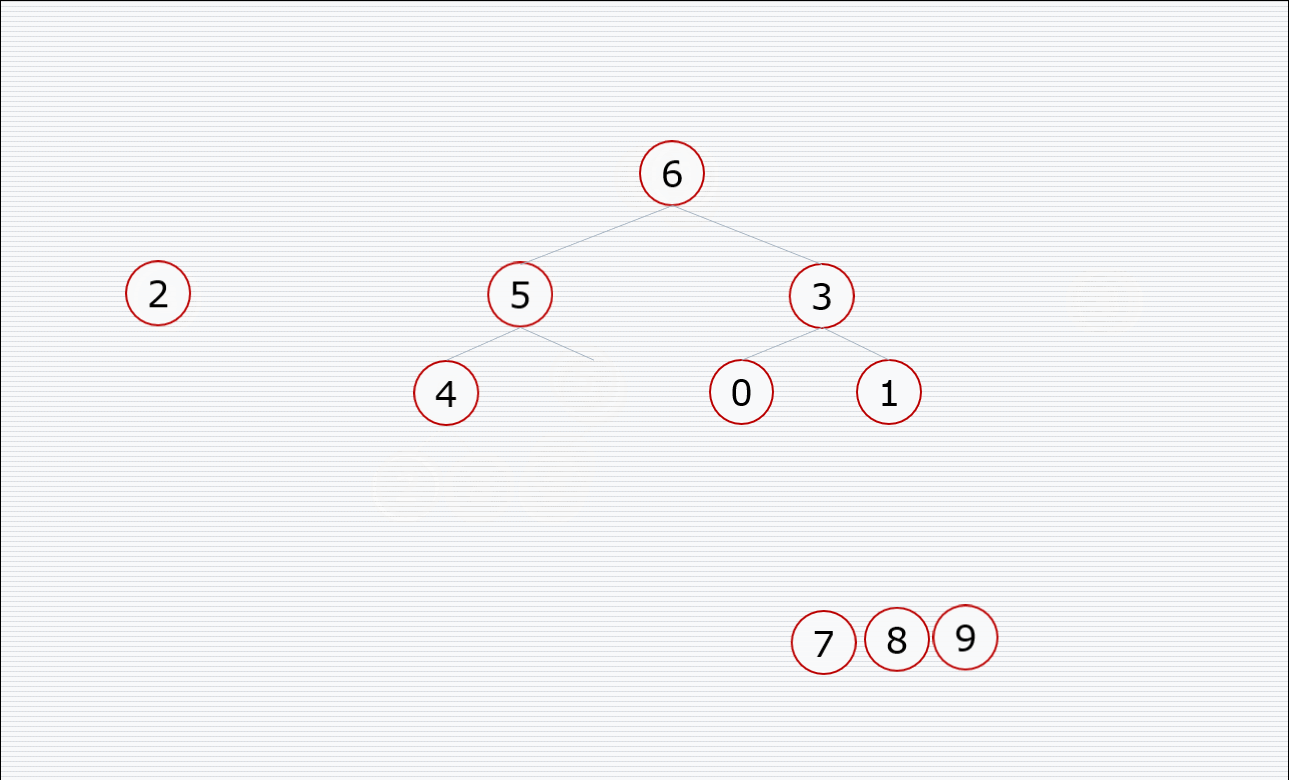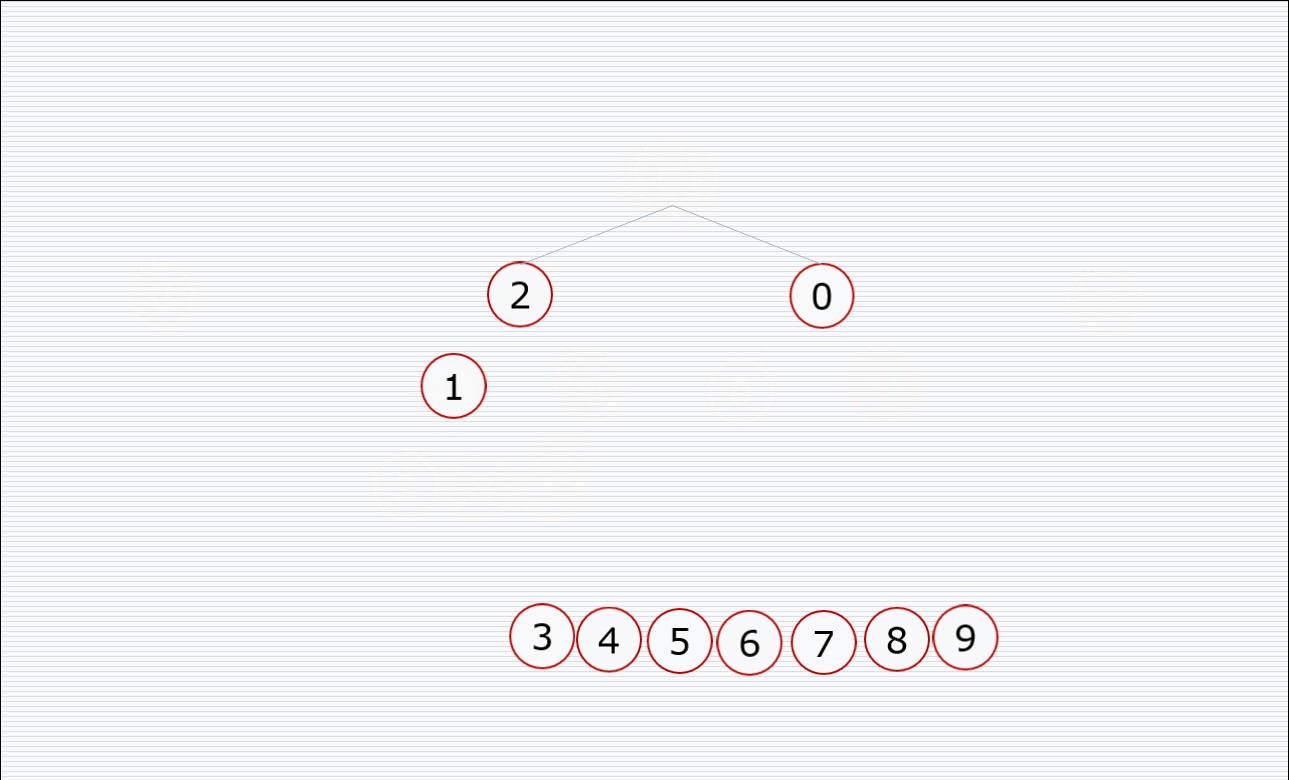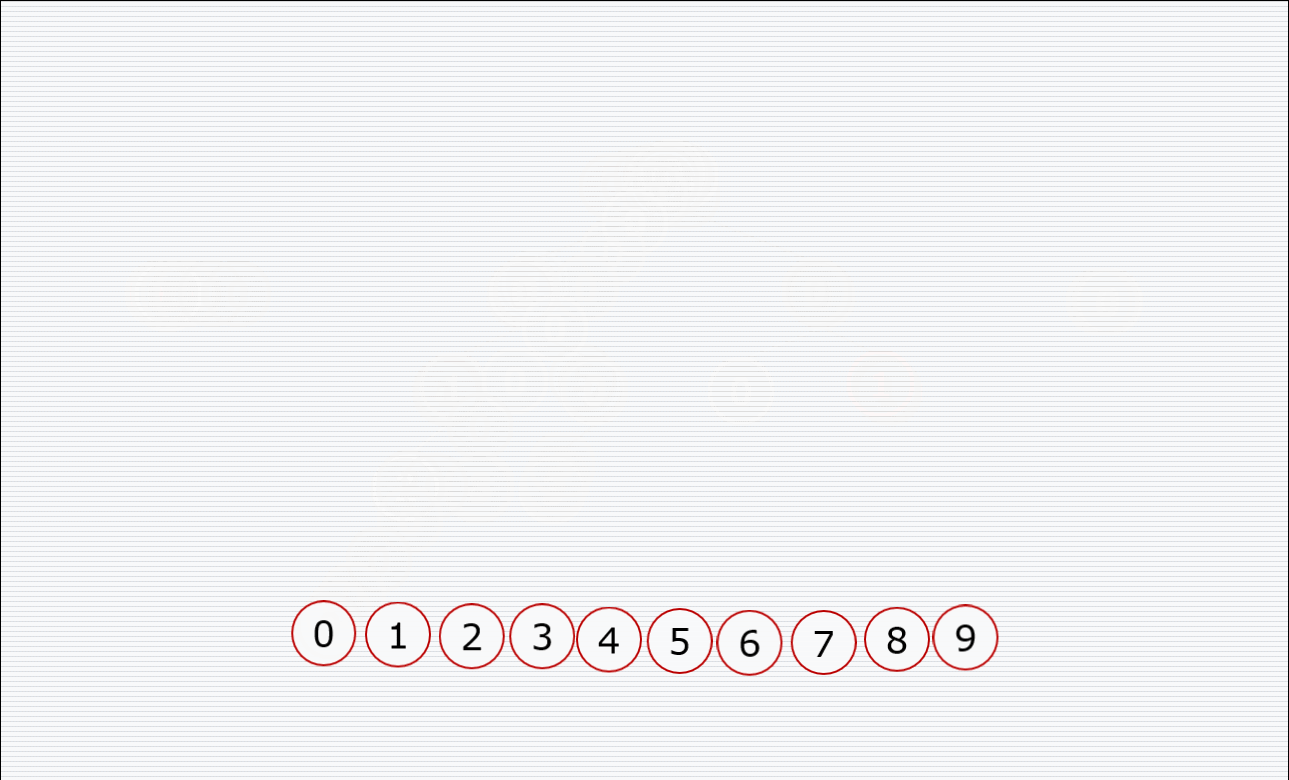
代码：

def sift(li, left, right):  # left和right 表示了元素的范围，是根节点到右节点的范围，然后比较根和两个孩子的大小，把大的放到堆顶
                                    # 和两个孩子的大小没关系，因为我们只需要拿堆顶的元素就行了
    # 构造堆
    i = left        # 当作根节点
    j = 2 * i + 1   # 上面提到过的父节点与左子树根节点的编号下标的关系
    tmp = li[left]
    while j <= right:
        if j+1 <= right and li[j] < li[j+1]:    # 找到两个孩子中比较大的那个
            j = j + 1
        if tmp < li[j]:     # 如果孩子中比较大的那个比根节点大，就交换
            li[i] = li[j]
            i = j           # 把交换了的那个节点当作根节点，循环上面的操作
            j = 2 * i + 1
        else:
            break
    li[i] = tmp             # 如果上面发生交换，现在的i就是最后一层符合条件（不用换）的根节点，

def heap_sort(li):
    n = len(li)
    for i in range(n//2-1, -1, -1):  # 建立堆        n//2-1 是为了拿到最后一个子树的根节点的编号，然后往前走，最后走到根节点0//2 -1 = -1
        sift(li, i, n-1)                # 固定的把最后一个值的位置当作right，因为right只是为了判断递归不要超出当前树，所以最后一个值可以满足
                                                    # 如果每遍历一个树，就找到它的右孩子，太麻烦了
    for i in range(n-1, -1, -1):    # 挨个出数
        li[0], li[i] = li[i],li[0]      # 把堆顶与最后一个数交换，为了节省空间，否则还可以新建一个列表，把堆顶（最大数）放到新列表中
        sift(li, 0, i-1)            # 此时的列表，应该排除最后一个已经排好序的，放置最大值的位置，所以i-1

时间复杂度也是O(nlogn)

来扩展一下，如果要取一个列表的top10，就是取列表的前十大的数，怎么做？

可以用堆来实现，取堆的前十个数，构造成一个小根堆，然后依次遍历列表后面的数，如果比堆顶小，则忽略，如果比堆顶大，则将堆顶替换成改元素，然后进行一次向下调整，最终这个小根堆就是top10

其实Python自带一个heapq模块，就是帮我们对堆进行操作的

heapq模块

队列中的每个元素都有优先级，优先级最高的元素优先得到服务（操作），这就是优先队列，而优先队列通常用堆来实现

如果用heapq模块来实现堆排序，就简单多了：

import heapq
def heapq_sort(li):
    h = []
    for value in li:
        heapq.heappush(h,value)
    return [heapq.heappop(h) for i in range(len(h))]

而想取top10 ，直接一个方法就行了

heapq.nlargest(10,li)

这三种速度快的排序方式就说完了，其中，快排是速度最快的，即使这样，也不如Python自带的sort快

再来介绍两种排序，希尔排序和计数排序

7.希尔排序

希尔排序是一种分组插入排序的算法　　

思路：

　　首先取一个整数d1=n/2，将元素分为d1个组，每组相邻量元素之间距离为d1，在各组内进行直接插入排序；

　　取第二个整数d2=d1/2，重复上述分组排序过程，直到di=1，即所有元素在同一组内进行直接插入排序。

希尔排序每趟并不使某些元素有序，而是使整体数据越来越接近有序；最后一趟排序使得所有数据有序。

图示：

　

代码：

def shell_sort(li):
    gap = int(len(li)//2)   # 初始把列表分成 gap个组，但是每组最多就两个元素，第一组可能有三个元素
    while gap >0:
        for i in range(gap,len(li)):
            tmp = li[i]
            j = i - gap
            while j>0 and tmp<li[j]:    # 对每一组的每一个数，都和他前面的那个数比较，小的在前面
                li[j+gap] = li[j]
                j -= gap
            li[j+gap] = tmp
        gap = int(gap//2)　　　　# Python3中地板除也是float类型
    return li

　　通过diamante也能看出来，其实希尔排序和插入排序是非常相像的，插入排序就可以看做是固定间隔为1的希尔排序，希尔排序就是把插入排序分了个组，同一个组内，相邻两个数之间不是相差1，而是相差gap

时间复杂度：O((1+t)n)，其中t是个大于0小于1的数，取决于gap的取法，当gap=len(li)//2的时候，t大约等于0.3

8.计数排序

需求：有一个列表，列表中的数都在0到100之间（整数），列表长度大约是100万，设计算法在O(n)时间复杂度内将列表进行排序

分析：列表长度很大，但是数据量很少，会有大量的重复数据。可以考虑对这100个数进行排序

代码：

def count_sort(li):
    count = [0 for i in range(101)]  # 根据原题，0-100的整数
    for i in li:
        count[i] += 1

    i = 0
    for num,m in enumerate(count):  # enumerate函数将一个可遍历的数据对象(如列表、元组或字符串)组合为一个索引序列，同时列出数据和数据下标，一般用在 for 循环当中。
        for j in range(m):
            li[i] = num
            i += 1

 此文摘抄来自    http://www.cnblogs.com/zhang-can/p/8011002.html   
抄过来的目的是为了学习，并不是炫耀什么的，不喜勿喷，谢谢