UVA 10382 - Watering Grass【贪心+区间覆盖问题+高精度】

UVa 10382 - Watering Grass

n sprinklers are installed in a horizontal strip of grass l meters long and w meters wide. Each sprinkler is installed at the horizontal center line of the strip. For each sprinkler we are given its position as the distance from the left end of the center line and its radius of operation.

What is the minimum number of sprinklers to turn on in order to water the entire strip of grass?

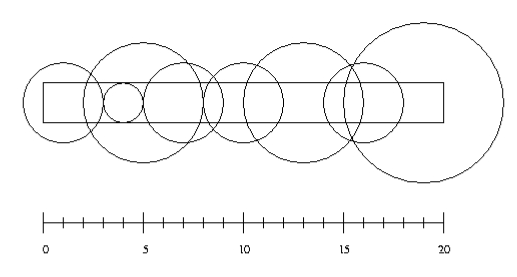
Input

Input consists of a number of cases. The first line for each case contains integer numbers n, l and w with n <= 10000. The next n lines contain two integers giving the position of a sprinkler and its radius of operation. (The picture above illustrates the first case from the sample input.)

Output

For each test case output the minimum number of sprinklers needed to water the entire strip of grass. If it is impossible to water the entire strip output -1.

Sample input

8 20 2

5 3

4 1

1 2

7 2

10 2

13 3

16 2

19 4

3 10 1

3 5

9 3

6 1

3 10 1

5 3

1 1

9 1

Sample output

6

2

-1

题目链接：http://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&category=113&page=show_problem&problem=1323

题目大意：

有一块草坪，长为l，宽为w，在它的水平中心线上有n个位置可以安装喷水装置，各个位置上的喷水装置的覆盖范围为以它们自己的半径ri为圆。求出最少需要的喷水装置个数。

分析与总结：

这题的关键在于转化

根据这图可以看出，一个喷水装置的有效覆盖范围就是圆中间的那个矩形。所以，在输入的同时，进行预处理，转换成矩形左边的坐标和右边的坐标。 这样，其实就转换成了经典的区间覆盖问题。

下面给出AC代码：

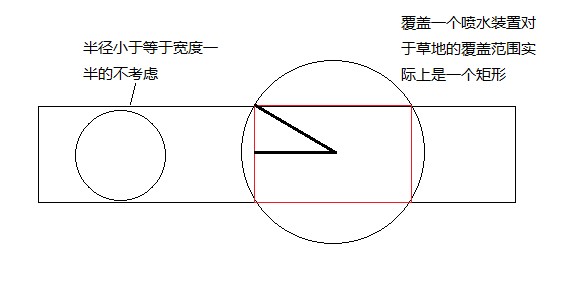
 #include <bits/stdc++.h>
 using namespace std;
 inline int read()
 {
     int x=,f=;
     char ch=getchar();
     while(ch<''||ch>'')
     {
         if(ch=='-')
             f=-;
         ch=getchar();
     }
     while(ch>=''&&ch<='')
     {
         x=x*+ch-'';
         ch=getchar();
     }
     return x*f;
 }
 inline void write(int x)
 {
     if(x<)
     {
         putchar('-');
         x=-x;
     }
     if(x>)
     {
         write(x/);
     }
     putchar(x%+'');
 }
 struct Node
 {
     double x,y;
 }p[];
 int cmp(const Node &a,const Node &b)
 {
     if(a.x<b.x)
     return ;
     else
     return ;
 }
 int main()
 {
     int n;
     double l,w;
     while(scanf("%d%lf%lf",&n,&l,&w)!=EOF)
     {
         for(int i=;i<n;i++)
         {
             double s,r;
             scanf("%lf%lf",&s,&r);
             if(r<w/2.0-1e-||fabs(r-w/2.0)<1e-)
             {
                 i--;
                 n--;
                 continue;
             }
             double x=sqrt(r*r-w*w/4.0);
             p[i].x=s-x;
             p[i].y=s+x;
             if(p[i].x<1e-)
             p[i].x=;
             if(p[i].y>l+1e-)
             p[i].y=l;
         }
         sort(p,p+n,cmp);
         if(fabs(p[].x)>1e-)
         {
             printf("-1\n");
             continue;
         }
         double pos=,maxx=;
         int sum=;
         while()
         {
             if(pos>=l)
             break;
             maxx=;
             for(int i=;i<n;i++)
             if((p[i].x<pos-1e-||fabs(p[i].x-pos)<1e-)&&p[i].y>pos+1e-)
             {
                 if(p[i].y>maxx+1e-)
                 {
                     maxx=p[i].y;
                 }
             }
             if(fabs(maxx)<1e-)
             {
                 sum=;
                 break;
             }
             sum++;
             pos=maxx;
         }
         if(sum==)
         printf("-1\n");
         else
         printf("%d\n",sum);
     }
     return ;
 }