计蒜客蓝桥杯模拟赛五J. 程序设计：放置守卫

在一张 n 行 m 列的方格地图上放置一些守卫，每个守卫能守护上、左、右三个方向上相邻的方格和自己所在的方格。如下图，红色的方格放置守卫，绿色的方格为该守卫守护的区域。

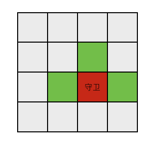
现在要求在地图上放置若干个守卫，让每个方格至少被一个守卫守护（可以同时被多个守卫守护），但是有些方格上不能放置守卫（这个方格也需要被守护），求出最少需要多少个守卫才能满足条件。

输入格式

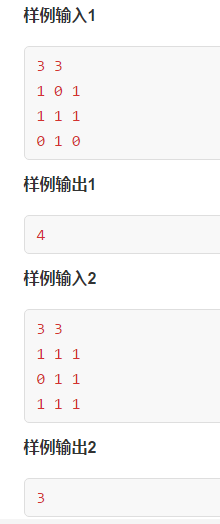
第一行输入两个整数 n, m。

接下来输入一个 n×m 的矩阵。矩阵中元素为 0 表示该位置不能放置守卫，为 1 表示该位置能放置守卫。元素之间用空格隔开。

数据约定： 所有数据保证一定有一种方案满足条件。

对于 20% 的数据： 1≤n,m≤5；

对于 50% 的数据： 1≤n≤20,1≤m≤10；

对于100% 的数据： 1≤n∗m≤1000,1≤m≤15。

输出格式

输出最少需要放置的守卫数量。

没有打这个。。不过学校群有人发出来了。做了下，没得交，大概思路应该是对的

做法：

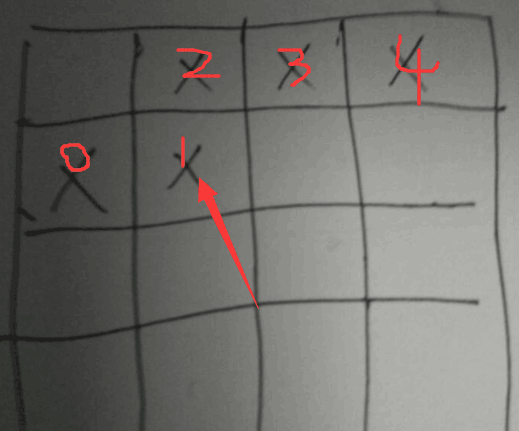
我们做一个dp，假设格子移动到了图中标记为1的地方，我们定义dp[now][sta]为当移动到这个格子，而且(4,3,2,1,0)的状态为sta的二进制表示（顺序也是一样的，1表示已放置，0表示未放置），并且这个分界线以上的全部被放置了的最小放置守卫数，这个分界线是这样的，当转移到（i，j）时，分界线就是(i,0)(i,1)...(i,j)(i-1,j)(i-1,j+1)..(i-1,m-1)转移比较简单，初始化第一个格子的时候，我们知道第一个格子是没有格子的，但是我们把那里当成已被守卫的格子就好了所以就是dp[now][(1 << m+1) - 2] = 0,其他定义为-1。

举个例子吧,下面的数字外面一层表示行列数，里面的表示分界线

0 1 2 3

0  _ _ 3 4

1  0 1 2 _

图1

我们知道我们当前是转移到(1,2)这个位置的，当这个位置可以放守卫，我们选择放一个守卫之后

0 1 2 3

0  _ _ _ 4

1  0 1 2 3

图2

现在转移到下一个格子了，但是刚刚在(1,2)放了守卫，所以(1,1)(1,2)(1,3)(0,2)这四个位置的状态都要变成了1，所以我们的sta需要或一个(1 << (j-1))(1 << (j))(1 << (j+1))如果j-1小于0就不用了，(0,2)这个位置已经到了分界线外。所以如果当前格子上面是没有守卫的，就必须放一个。因为我们定义的dp是分界线上必须全部被守卫。

如果当前格子有守卫，我们可以选择不放，如果不放的话我们需要把sta^(1 << (j + 1))，因为我们可以知道图1的分界线3转移到下一个的图2时，这个位置原本是没有守卫的，所以要置为0。

这上面的转移是一种情况，但是当转移需要换行的时候，转移的式子会有所改变，不过手推很容易推出来。

#include <cstdio>
#include <cstring>
#include <cmath>
#include <queue>
#include <vector>
#include <time.h>
#include <string>
#include <stack>
#include <set>
#include <map>
#include <iostream>
#include <bitset>
#include <algorithm>
using namespace std;
#define MP make_pair
#define rep(i,n) for(int i = 0; i < (n); i++)
#define per(i,n) for(int i = (n-1); i >= 0; i--)
#define rep1(i,n) for(int i = 1; i <= (n); i++)
#define per1(i,n) for(int i = (n); i > 0; i--)

#define PB push_back
#define mst(a,b) memset((a),(b),sizeof(a))
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> Pii;
typedef vector<int> Vi;
typedef vector<Pii> Vii;
const int inf = 0x3f3f3f3f;
const LL INF = (1uLL << ) - ;
const LL mod = ;
const int N = 1e5 + ;
const double Pi = acos(-1.0);
const int maxn = ( << ) + ;
const uLL Hashmod = ;
int dp[][maxn];
int maz[][];
int n, m;
inline bool up(int sta, int pos) {
    return (sta & ( << (pos + ))) != ;
}
inline void uMin(int &A, int B) {
    if(B == -)return;
    if(A == -)A = B;
    else A = min(A, B);
}
inline int Set(int sta, int pos) {
    if(pos -  >= )sta |= ( << (pos - ));
    sta |= ( << pos);
    sta |= ( << (pos + ));
    if(pos == m - ) {
        sta <<= ;
        sta %= ( << (m + ));
    }
    return sta;
}
inline int noSet(int sta,int pos){
    if(pos != m - )sta ^= ( << (pos + ));
    else sta <<= ,sta %= ( << (m + ));
    return sta;
}
//inline void show(int x) {
//    putchar('0' + x % 2);
//    if(x > 1)show(x / 2);
//}
int main() {
#ifdef local
    freopen("input", "r", stdin);
    //freopen("w","w",stdout);
#endif
    ios::sync_with_stdio();
    cin.tie();
    cin >> n >> m;
    rep(i, n)rep(j, m)cin >> maz[i][j];
    int nx = , now = ;
    mst(dp[nx], -);
    dp[nx][( << (m + )) - ] = ;
    rep(i, n) {
        rep(j, m) {
            swap(nx, now);
            mst(dp[nx], -);
            rep(sta, ( << (m + ))) {
                if(dp[now][sta] != -) {
                    if(up(sta, j)) uMin(dp[nx][noSet(sta,j)], dp[now][sta]);
                    if(maz[i][j]) uMin(dp[nx][Set(sta, j)], dp[now][sta] + );
                }
            }
        }
    }
    int ans = dp[now][( << (m + )) - ];
    uMin(ans,dp[nx][( << (m + )) - ]);
    cout << ans << endl;
}

...因为并没有找到可以提交的地方，所以代码也只是随便测了几组，不过思路好像没什么问题，如果找到代码错误的话可以留言或者私信交流一下