随机抽样一致算法（Random sample consensus，RANSAC）

作者：桂。

时间：2017-04-25  21:05:07

链接：http://www.cnblogs.com/xingshansi/p/6763668.html

---

前言

仍然是昨天的问题，别人问到最小二乘、霍夫变换、RANSAC在直线拟合上的区别。昨天梳理了霍夫变换，今天打算抽空梳理一下RANSAC算法，主要包括：

　　1）RANSAC理论介绍

　　2）RANSAC应用简介；

内容为自己的学习记录，其中很多地方借鉴了别人，最后一起给出链接。

一、RANSAC理论介绍

普通最小二乘是保守派：在现有数据下，如何实现最优。是从一个整体误差最小的角度去考虑，尽量谁也不得罪。

RANSAC是改革派：首先假设数据具有某种特性（目的），为了达到目的，适当割舍一些现有的数据。

给出最小二乘拟合（红线）、RANSAC（绿线）对于一阶直线、二阶曲线的拟合对比：

可以看到RANSAC可以很好的拟合。RANSAC可以理解为一种采样的方式，所以对于多项式拟合、混合高斯模型（GMM）等理论上都是适用的。

RANSAC的算法大致可以表述为（来自wikipedia）：

Given:
    data – a set of observed data points
    model – a model that can be fitted to data points
    n – the minimum number of data values required to fit the model
    k – the maximum number of iterations allowed in the algorithm
    t – a threshold value for determining when a data point fits a model
    d – the number of close data values required to assert that a model fits well to data

Return:
    bestfit – model parameters which best fit the data (or nul if no good model is found)

iterations = 0
bestfit = nul
besterr = something really large
while iterations < k {
    maybeinliers = n randomly selected values from data
    maybemodel = model parameters fitted to maybeinliers
    alsoinliers = empty set
    for every point in data not in maybeinliers {
        if point fits maybemodel with an error smaller than t
             add point to alsoinliers
    }
    if the number of elements in alsoinliers is > d {
        % this implies that we may have found a good model
        % now test how good it is
        bettermodel = model parameters fitted to all points in maybeinliers and alsoinliers
        thiserr = a measure of how well model fits these points
        if thiserr < besterr {
            bestfit = bettermodel
            besterr = thiserr
        }
    }
    increment iterations
}
return bestfit

RANSAC简化版的思路就是：

第一步：假定模型（如直线方程），并随机抽取Nums个（以2个为例）样本点，对模型进行拟合：

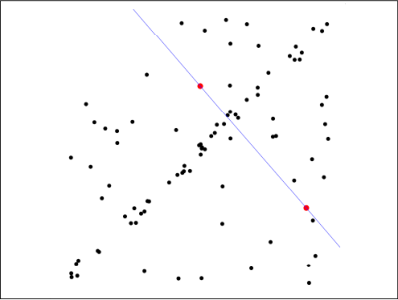
第二步：由于不是严格线性，数据点都有一定波动，假设容差范围为：sigma，找出距离拟合曲线容差范围内的点，并统计点的个数：

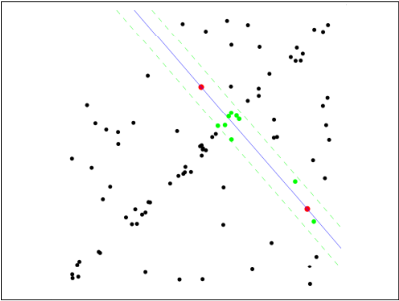
第三步：重新随机选取Nums个点，重复第一步~第二步的操作，直到结束迭代：

第四步：每一次拟合后，容差范围内都有对应的数据点数，找出数据点个数最多的情况，就是最终的拟合结果：

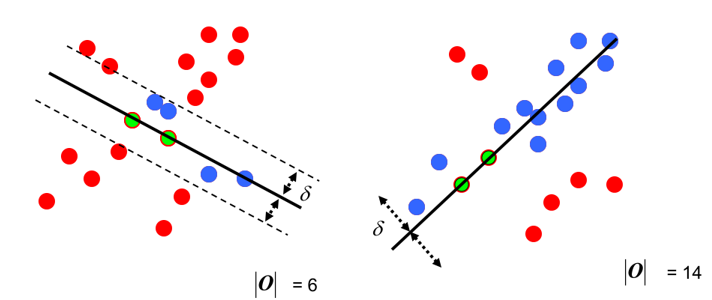
至此：完成了RANSAC的简化版求解。

这个RANSAC的简化版，只是给定迭代次数，迭代结束找出最优。如果样本个数非常多的情况下，难不成一直迭代下去？其实RANSAC忽略了几个问题：

• 每一次随机样本数Nums的选取：如二次曲线最少需要3个点确定，一般来说，Nums少一些易得出较优结果；
• 抽样迭代次数Iter的选取：即重复多少次抽取，就认为是符合要求从而停止运算？太多计算量大，太少性能可能不够理想；
• 容差Sigma的选取：sigma取大取小，对最终结果影响较大；

这些参数细节信息参考：维基百科。

RANSAC的作用有点类似：将数据一切两段，一部分是自己人，一部分是敌人，自己人留下商量事，敌人赶出去。RANSAC开的是家庭会议，不像最小二乘总是开全体会议。

附上最开始一阶直线、二阶曲线拟合的code(只是为了说明最基本的思路，用的是RANSAC的简化版):

一阶直线拟合：

clc;clear all;close all;
 set(0,'defaultfigurecolor','w');
%Generate data
param = [3 2];
npa = length(param);
x = -20:20;
y = param*[x; ones(1,length(x))]+3*randn(1,length(x));
data = [x randi(20,1,30);...
    y randi(20,1,30)];
%figure
figure
subplot 221
plot(data(1,:),data(2,:),'k*');hold on;
%Ordinary least square mean
p = polyfit(data(1,:),data(2,:),npa-1);
flms = polyval(p,x);
plot(x,flms,'r','linewidth',2);hold on;
title('最小二乘拟合');
%Ransac
Iter = 100;
sigma = 1;
Nums = 2;%number select
res = zeros(Iter,npa+1);
for i = 1:Iter
idx = randperm(size(data,2),Nums);
if diff(idx) ==0
    continue;
end
sample = data(:,idx);
pest = polyfit(sample(1,:),sample(2,:),npa-1);%parameter estimate
res(i,1:npa) = pest;
res(i,npa+1) = numel(find(abs(polyval(pest,data(1,:))-data(2,:))<sigma));
end
[~,pos] = max(res(:,npa+1));
pest = res(pos,1:npa);
fransac = polyval(pest,x);
%figure
subplot 222
plot(data(1,:),data(2,:),'k*');hold on;
plot(x,flms,'r','linewidth',2);hold on;
plot(x,fransac,'g','linewidth',2);hold on;
title('RANSAC');

　　二阶曲线拟合：

clc;clear all;
 set(0,'defaultfigurecolor','w');
%Generate data
param = [3 2 5];
npa = length(param);
x = -20:20;
y = param*[x.^2;x;ones(1,length(x))]+3*randn(1,length(x));
data = [x randi(20,1,30);...
    y randi(200,1,30)];
%figure
subplot 223
plot(data(1,:),data(2,:),'k*');hold on;
%Ordinary least square mean
p = polyfit(data(1,:),data(2,:),npa-1);
flms = polyval(p,x);
plot(x,flms,'r','linewidth',2);hold on;
title('最小二乘拟合');
%Ransac
Iter = 100;
sigma = 1;
Nums = 3;%number select
res = zeros(Iter,npa+1);
for i = 1:Iter
idx = randperm(size(data,2),Nums);
if diff(idx) ==0
    continue;
end
sample = data(:,idx);
pest = polyfit(sample(1,:),sample(2,:),npa-1);%parameter estimate
res(i,1:npa) = pest;
res(i,npa+1) = numel(find(abs(polyval(pest,data(1,:))-data(2,:))<sigma));
end
[~,pos] = max(res(:,npa+1));
pest = res(pos,1:npa);
fransac = polyval(pest,x);
%figure
subplot 224
plot(data(1,:),data(2,:),'k*');hold on;
plot(x,flms,'r','linewidth',2);hold on;
plot(x,fransac,'g','linewidth',2);hold on;
title('RANSAC');

　　

二、RANSAC应用简介

RANSAC其实就是一种采样方式，例如在图像拼接（Image stitching）技术中：

第一步：预处理后（据说桶形变换，没有去了解过）提取图像特征（如SIFT）

第二步：特征点进行匹配，可利用归一化互相关(Normalized Cross Correlation method, NCC)等方法。

但这个时候会有很多匹配错误的点：

这就好比拟合曲线，有很多的误差点，这个时候就想到了RANSAC算法：我不要再兼顾所有了，每次选取Nums个点匹配 → 计算匹配后容差范围内的点数 → 重复实验，迭代结束后，找出点数最多的情况，就是最优的匹配。 

利用RANSAC匹配：

第三步：图像拼接，这个就涉及拼接技术了，直接给出结果：

参考：

• RANSAC：https://en.wikipedia.org/wiki/Random_sample_consensus
• 图像拼接：http://blog.csdn.net/xiaoch1222/article/details/53510895