K：图相关的最小生成树（MST）

相关介绍:

 根据树的特性可知，连通图的生成树是图的极小连通子图，它包含图中的全部顶点，但只有构成一棵树的边；生成树又是图的极大无回路子图，它的边集是关联图中的所有顶点而又没有形成回路的边。

 一个有n个顶点的连通图的生成树只有n-1条边。若有n个顶点而少于n-1条边，则是非连通图(将其想成有n个顶点的一条链，则其为连通图的条件是至少有n-1条边)；若多于n-1条边，则一定形成回路。值得注意的是，有n-1条边的生成子图，并不一定是生成树。此处，介绍一个概念。网：指的是边带有权值的图。

 在一个网的所有生成树中，权值总和最小的生成树，称之为最小代价生成树，也称为最小生成树。

最小生成树:

 根据生成树的定义，具有n个顶点的连通图的生成树，有n个顶点和n-1条边。因此，构造最小生成树的准则有以下3条:

1. 只能使用图中的边构造最小生成树
2. 当且仅当使用n-1条边来连接图中的n个顶点
3. 不能使用产生回路的边

需要注意的一点是，尽管最小生成树一定存在，但其并不一定是唯一的。以下介绍求图的最小生成树的两个典型的算法，分别为克鲁斯卡尔算法(kruskal)和普里姆算法(prim)

克鲁斯卡尔(Kruskal)算法：

 克鲁斯卡尔算法是根据边的权值递增的方式，依次找出权值最小的边建立的最小生成树，并且规定每次新增的边，不能造成生成树有回路，直到找到n-1条边为止。

基本思想：设图G=（V,E）是一个具有n个顶点的连通无向网，T=（V,TE）是图的最小生成树，其中V是T的顶点集，TE是T的边集，则构造最小生成树的具体步骤如下：

1. T的初始状态为T=（V,空集），即开始时，最小生成树T是图G的生成零图

2. 将图G中的边按照权值从小到大的顺序依次选取，若选取的边未使生成树T形成回路，则加入TE中，否则舍弃，直至TE中包含了n-1条边为止

下图演示克鲁斯卡尔算法的构造最小生成树的过程:

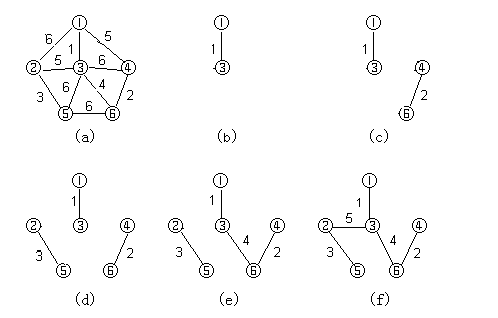
其示意代码如下:

相关代码：

package all_in_tree;

import java.util.Comparator;
import java.util.PriorityQueue;
import java.util.Queue;

import algorithm.PathCompressWeightQuick_Union;
import algorithm.UF;

/**
 * 该类用于演示克鲁斯卡尔算法的过程
 * @author 学徒
 *
 *由于每次添加一条边时，需要判断所添加的边是否会产生回路，而回路的产生，当且仅当边上的两个节点处在同一个连通
 *分支上，为此，可以使用Union-Find算法来判断边上的两个点是否处在同一个连通分支上
 *
 */
public class Kruskal
{
	//用于记录节点的数目
	private int nodeCount;
	//用于判断是否会形成回路
	private UF unionFind;
	//用优先级队列，每次最先出队的是其权值最小的边
	private Queue<Edge> q;
	//用于存储图的生成树
	private Edge[] tree;
	/**
	 * 初始化一个图的最小生成树所需的数据结构
	 * @param n 图的节点的数目
	 */
	public Kruskal(int n)
	{
		this.nodeCount=n;
		tree=new Edge[n-1];
		unionFind=new PathCompressWeightQuick_Union(n);
		Comparator<Edge> cmp=new Comparator<Edge>()
		{
			@Override
			public int compare(Edge obj1,Edge obj2)
			{
				int obj1W=obj1.weight;
				int obj2W=obj2.weight;
				if(obj1W<obj2W)
					return -1;
				else if(obj1W>obj2W)
					return 1;
				else
					return 0;
			}
		};
		q=new PriorityQueue<Edge>(11,cmp);
	}
	/**
	 * 用于添加一条边
	 * @param edge 所要进行添加的边
	 */
	public void addEdge(Edge edge)
	{
		q.add(edge);
	}

	/**
	 * 用于生成最小生成树
	 * @return 最小生成树的边集合
	 */
	public Edge[] getTree()
	{
		//用于记录加入图的最小生成树的边的数目
		int edgeCount=0;
		//用于得到最小生成树
		while(!q.isEmpty()&&edgeCount<this.nodeCount-1)
		{
			//每次取出权值最小的一条边
			Edge e=q.poll();
			//判断是否产生回路，当其不产生回路时，将其加入到最小生成树中
			int index1=unionFind.find(e.node1);
			int index2=unionFind.find(e.node2);
			if(index1!=index2)
			{
				tree[edgeCount++]=e;
				unionFind.union(e.node1, e.node2);
			}
		}
		return tree;
	}
}

/**
 * 测试用例所使用的类，该类的测试用例即为上图中中所示的Kruskal算法最小生成树的构造
 * 过程的示例图，且其节点编号从0开始，而不从1开始
 * @author 学徒
 *
 */
class Test
{
	public static void main(String[] args)
	{
		Kruskal k=new Kruskal(6);
		k.addEdge(new Edge(0,3,5));
		k.addEdge(new Edge(0,1,6));
		k.addEdge(new Edge(1,4,3));
		k.addEdge(new Edge(4,5,6));
		k.addEdge(new Edge(3,5,2));
		k.addEdge(new Edge(0,2,1));
		k.addEdge(new Edge(1,2,5));
		k.addEdge(new Edge(2,4,6));
		k.addEdge(new Edge(2,5,4));
		k.addEdge(new Edge(2,3,6));
		Edge[] tree=k.getTree();
		for(Edge e:tree)
		{
			System.out.println(e.node1+" --> "+e.node2+"  : "+e.weight);
		}
	}
}

/**
 * 图的边的数据结构
 * @author 学徒
 *
 */
class Edge
{
	//节点的编号
	int node1;
	int node2;
	//边上的权值
	int weight;

	public Edge()
	{
	}
	public Edge(int node1,int node2,int weight)
	{
		this.node1=node1;
		this.node2=node2;
		this.weight=weight;
	}
}

运行结果：
0 --> 2  : 1
3 --> 5  : 2
1 --> 4  : 3
2 --> 5  : 4
1 --> 2  : 5

ps:上述代码中所用到的Union-Find算法的相关代码及解析，请点击 K：Union-Find（并查集）算法 进行查看

分析 :该算法的时间复杂度为O（elge）,即克鲁斯卡尔算法的执行时间主要取决于图的边数e，为此，该算法适用于针对稀疏图的操作

普里姆算法(Prim)：

 为描述的方便，在介绍普里姆算法前，给出如下有关距离的定义：

1. 两个顶点之间的距离：是指将顶点u邻接到v的关联边的权值，即为|u,v|。若两个顶点之间无边相连，则这两个顶点之间的距离为无穷大

2. 顶点到顶点集合之间的距离：顶点u到顶点集合V之间的距离是指顶点u到顶点集合V中所有顶点之间的距离中的最小值，即为|u,V|=\(min|u,v| , v\in V\)

3. 两个顶点集合之间的距离：顶点集合U到顶点集合V的距离是指顶点集合U到顶点集合V中所有顶点之间的距离中的最小值，记为|U,V|=\(min|u,V| , u\in U\)

基本思想：假设G=（V,E）是一个具有n个顶点的连通网，T=（V，TE）是网G的最小生成树。其中，V是R的顶点集，TE是T的边集，则最小生成树的构造过程如下:从U={u0},TE=\(\varnothing\)开始，必存在一条边（u，v），u\(\in U\),v\(\in V-U\)，使得|u，v|=|U，V-U|，将（u，v）加入集合TE中，同时将顶点v*加入顶点集U中，直到U=V为止，此时，TE中必有n-1条边(最小生成树存在的情况)，最小生成树T构造完毕。下图演示了使用Prim算法构造最小生成树的过程

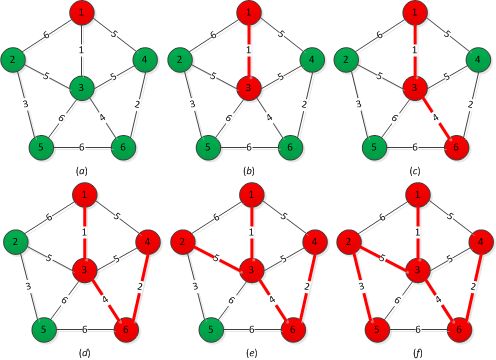
其示意代码如下:

相关代码：

package all_in_tree;
/**
 * 该类用于演示Prim算法构造最小生成树的过程
 * @author 学徒
 *
 */
public class Prim
{
	//用于记录图中节点的数目
	private int nodeCount;
	//用于记录图的领接矩阵，其存储对应边之间的权值
	private int[][] graph;
	//用于记录其对应节点是否已加入集合U中，若加入了集合U中，则其值为true
	private boolean[] inU;
	//用于记录其生成的最小生成树的边的情况
	private Edge[] tree;
	//用于记录其下标所对的节点的编号相对于集合U的最小权值边的权值的情况
	private int[] min;
	//用于记录其下标所对的节点的最小权值边所对应的集合U中的节点的情况
	private int[] close;
	/**
	 * 用于初始化
	 * @param n 节点的数目
	 */
	public Prim(int n)
	{
		this.nodeCount=n;
		this.graph=new int[n][n];
		//初始化的时候，将各点的权值初始化为最大值
		for(int i=0;i<n;i++)
		{
			for(int j=0;j<n;j++)
			{
				graph[i][j]=Integer.MAX_VALUE;
			}
		}
		this.inU=new boolean[n];
		this.tree=new Edge[n-1];
		this.min=new int[n];
		this.close=new int[n];
	}

	/**
	 *用于为图添加一条边
	 * @param edge 边的封装类
	 */
	public void addEdge(Edge edge)
	{
		int node1=edge.node1;
		int node2=edge.node2;
		int weight=edge.weight;
		graph[node1][node2]=weight;
		graph[node2][node1]=weight;
	}

	/**
	 * 用于获取其图对应的最小生成树的结果
	 * @return 由最小生成树组成的边的集合
	 */
	public Edge[] getTree()
	{
		//用于将第一个节点加入到集合U中
		for(int i=1;i<nodeCount;i++)
		{
			min[i]=graph[0][i];
			close[i]=0;
		}
		inU[0]=true;
		//用于循环n-1次，每次循环添加一条边进最小生成树中
		for(int i=0;i<nodeCount-1;i++)
		{
			//用于记录找到的相对于集合U中的节点的最小权值的节点编号
			int node=0;
			//用于记录其相对于集合U的节点的最小的权值
			int mins=Integer.MAX_VALUE;
			//用于寻找其相对于集合U中最小权值的边
			for(int j=1;j<nodeCount;j++)
			{
				if(min[j]<mins&&!inU[j])
				{
					mins=min[j];
					node=j;
				}
			}
			//用于记录其边的情况
			tree[i]=new Edge(node,close[node],mins);
			//修改相关的状态
			inU[node]=true;
			//修改其相对于集合U的情况
			for(int j=1;j<nodeCount;j++)
			{
				if(!inU[j]&&graph[node][j]<min[j])
				{
					min[j]=graph[node][j];
					close[j]=node;
				}
			}
		}
		return tree;
	}
}

class Edge
{
	//节点的编号
	int node1;
	int node2;
	//边上的权值
	int weight;

	public Edge()
	{
	}
	public Edge(int node1,int node2,int weight)
	{
		this.node1=node1;
		this.node2=node2;
		this.weight=weight;
	}
}

/**
 * 测试用例所使用的类，该类的测试用例即为上图中中所示的Prim算法最小生成树的构造
 * 过程的示例图，且其节点编号从0开始，而不从1开始
 * @author 学徒
 *
 */
class Test
{
	public static void main(String[] args)
	{
		Prim k=new Prim(6);
		k.addEdge(new Edge(0,3,5));
		k.addEdge(new Edge(0,1,6));
		k.addEdge(new Edge(1,4,3));
		k.addEdge(new Edge(4,5,6));
		k.addEdge(new Edge(3,5,2));
		k.addEdge(new Edge(0,2,1));
		k.addEdge(new Edge(1,2,5));
		k.addEdge(new Edge(2,4,6));
		k.addEdge(new Edge(2,5,4));
		k.addEdge(new Edge(2,3,5));
		Edge[] tree=k.getTree();
		for(Edge e:tree)
		{
			System.out.println(e.node1+" --> "+e.node2+"  : "+e.weight);
		}
	}
}

运行结果如下:
2 --> 0  : 1
5 --> 2  : 4
3 --> 5  : 2
1 --> 2  : 5
4 --> 1  : 3

总结：kruskal算法的时间复杂度与求解最小生成树的图中的边数有关，而prim算法的时间复杂度与求解最小生成树的图中的节点的数目有关。为此，Kruskal算法更加适用于稀疏图，而prim算法适用于稠密图。当e>=n^{2时，kruskal算法比prim算法差，但当e=O(n}2)时，kruskal算法却比prim算法好得多。

回到目录|·(工)·）