OMP算法代码学习

正交匹配追踪(OMP)算法的MATLAB函数代码并给出单次测试例程代码

测量数M与重构成功概率关系曲线绘制例程代码

信号稀疏度K与重构成功概率关系曲线绘制例程代码

 

参考来源：http://blog.csdn.net/jbb0523/article/details/45130793

参考文献：Joel A. Tropp and Anna C. Gilbert. Signal Recovery From Random Measurements Via Orthogonal Matching Pursuit[J]. IEEETransactions on Information Theory, VOL. 53, NO. 12, DECEMBER 2007.

---

0、符号说明如下

　　压缩观测y=Φx，其中y为观测所得向量M×1，x为原信号N×1（M<<N）。x一般不是稀疏的，但在某个变换域Ψ是稀疏的，即x=Ψθ，其中θ为K稀疏的，即θ只有K个非零项。此时y=ΦΨθ，令A=ΦΨ，则y=Aθ。

        (1)y为观测所得向量，大小为M×1

 

        (2)x为原信号，大小为N×1

 

        (3)θ为K稀疏的，是信号在x在某变换域的稀疏表示

 

        (4)Φ称为观测矩阵、测量矩阵、测量基，大小为M×N

 

        (5)Ψ称为变换矩阵、变换基、稀疏矩阵、稀疏基、正交基字典矩阵，大小为N×N

 

        (6)A称为测度矩阵、传感矩阵、CS信息算子，大小为M×N

　　上式中，一般有K<<M<<N，后面三个矩阵各个文献的叫法不一，以后我将Φ称为测量矩阵、将Ψ称为稀疏矩阵、将A称为传感矩阵。

1、OMP重构算法流程

2、正交匹配追踪(OMP)MATLAB代码(CS_OMP.m)

function[theta]=CS_OMP(y,A,t)
%CS_OMP Summary of this function goes here
 %Version: 1.0 written by jbb0523 @2015-04-18
 %   Detailed explanation goes here
 %   y = Phi * x
 %   x = Psi * theta
 %   y = Phi*Psi * theta
 %   令 A = Phi*Psi, 则y=A*theta
 %   现在已知y和A，求theta
    [y_rows,y_columns]=size(y);
    ify_rows<y_columns
         y=y';%y should be a column vector
    end
    [M,N]=size(A);                            %传感矩阵A为M*N矩阵
     theta=zeros(N,1);                         %用来存储恢复的theta(列向量)
     At=zeros(M,t);                            %用来迭代过程中存储A被选择的列
     Pos_theta=zeros(1,t);                    %用来迭代过程中存储A被选择的列序号
     r_n=y;                                    %初始化残差(residual)为y
    forii=1:t                                  %迭代t次，t为输入参数
         product=A'*r_n;                       %传感矩阵A各列与残差的内积
        [val,pos]=max(abs(product));          %找到最大内积绝对值，即与残差最相关的列
         At(:,ii)=A(:,pos);                     %存储这一列
         Pos_theta(ii)=pos;                     %存储这一列的序号
         A(:,pos)=zeros(M,1);                   %清零A的这一列，其实此行可以不要，因为它与残差正交
                                                                  %y=At(:,1:ii)*theta，以下求theta的最小二乘解(Least Square)
         theta_ls=(At(:,1:ii)'*At(:,1:ii))^(-1)*At(:,1:ii)'*y;  %最小二乘解
                                                                 %At(:,1:ii)*theta_ls是y在At(:,1:ii)列空间上的正交投影
         r_n=y-At(:,1:ii)*theta_ls;             %更新残差
    end
     theta(Pos_theta)=theta_ls;                   %恢复出的theta
 end

3、OMP单次重构测试代码(CS_Reconstuction_Test.m)

代码中，直接构造一个K稀疏的信号，所以稀疏矩阵为单位阵。

%压缩感知重构算法测试
clear all;close all;clc;
M=64;%观测值个数
N=256;%信号x的长度
K=10;%信号x的稀疏度
Index_K=randperm(N);
x=zeros(N,1);
x(Index_K(1:K))=5*randn(K,1);%x为K稀疏的，且位置是随机的
Psi=eye(N);%x本身是稀疏的，定义稀疏矩阵为单位阵x=Psi*theta
Phi=randn(M,N);%测量矩阵为高斯矩阵
A=Phi*Psi;%传感矩阵
y=Phi*x;%得到观测向量y
%% 恢复重构信号x
tic
theta=CS_OMP(y,A,K);
x_r=Psi*theta;% x=Psi * theta
toc
%% 绘图
figure;
plot(x_r,'k.-');%绘出x的恢复信号
hold on;
plot(x,'r');%绘出原信号x
hold off;
legend('Recovery','Original')
fprintf('\n恢复残差：');
norm(x_r-x)%恢复残差

　　代码解释：上述代码是直接构造一个K稀疏的信号，接下来解释一下代码中是如何构造该稀疏信号的。

　　首先介绍一下randperm函数，即randm permutation随机排列、随机置换。功能是随机打乱一个数字序列，其内的参数决定了随机数的范围。

   　 Index_K = randperm(N); 指的是将1到256的数进行随机排列

　　初始化信号x：x = zeros(N,1); 

       x(Index_K(1:K)) = 5*randn(K,1)；等式右边比较好理解，即构造一个K*1的随机向量，接着解释等式左边，括号内Index_K（1:K）指的是选取随机排列后的数列的前K项，因为我们要构造的信号是K稀疏的，也就是只有K个项为非零元素。则我们要将等式右边产生的K个非零值随机的插到信号x的K个位置中，举个例子，比如经过排列后的Index_K（1:K）=12  56 30 17 5 2 6 98  200 85 ，则等式右边的K个非零值被放置在x的第12、56……的位置上。

　　接着解释最后一行代码，norm指的是范数的意思，在代码中求得是重构后的信号与原始信号的差值的一范数，一范数相当于求绝对值，据此求出误差。

　　运行结果如下：（信号为随机生成，所以每次结果均不一样）

　1）图：

 

　　2）Command Windows

Elapsed time is 0.849710 seconds.

       恢复残差：

       ans =

         5.5020e-015

4、测量数M与重构成功概率关系曲线绘制例程代码

这段代码真的是断断续续看了好久才明白，理解代码还是要分块分块搞懂

%压缩感知重构算法测试CS_Reconstuction_MtoPercentage.m
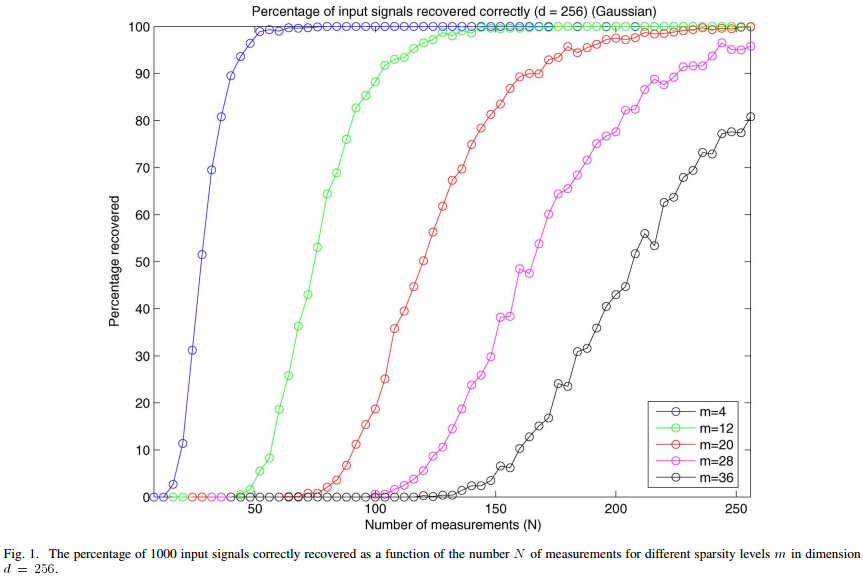
%   绘制参考文献中的Fig.1
%   参考文献：Joel A. Tropp and Anna C. Gilbert
%   Signal Recovery From Random Measurements Via Orthogonal Matching
%   Pursuit，IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 53, NO. 12,
%   DECEMBER 2007.
%   Elapsed time is 1171.606254 seconds.(@20150418night)
clear all;close all;clc;
%% 参数配置初始化
CNT=1000;%对于每组(K,M,N)，重复迭代次数
N=256;%信号x的长度
Psi=eye(N);%x本身是稀疏的，定义稀疏矩阵为单位阵x=Psi*theta
K_set=[4,12,20,28,36];%信号x的稀疏度集合
Percentage=zeros(length(K_set),N);%存储恢复成功概率
%% 主循环，遍历每组(K,M,N)
tic
forkk=1:5
    K=K_set(kk);%本次稀疏度
    M_set=K:5:N;%M没必要全部遍历，每隔5测试一个就可以了
    PercentageK=zeros(1,length(M_set));%存储此稀疏度K下不同M的恢复成功概率
   formm=1:length(M_set)
       M=M_set(mm);%本次观测值个数
       P=0;
      forcnt=1:CNT%每个观测值个数均运行CNT次
            Index_K=randperm(N);
            x=zeros(N,1);
            x(Index_K(1:K))=5*randn(K,1);%x为K稀疏的，且位置是随机的
            Phi=randn(M,N);%测量矩阵为高斯矩阵
            A=Phi*Psi;%传感矩阵
            y=Phi*x;%得到观测向量y
            theta=CS_OMP(y,A,K);%恢复重构信号theta
            x_r=Psi*theta;% x=Psi * theta
           ifnorm(x_r-x)<1e-6%如果残差小于1e-6则认为恢复成功
                P=P+1;
           end
      end
       PercentageK(mm)=P/CNT*100;%计算恢复概率
   end
    Percentage(kk,1:length(M_set))=PercentageK;
end
toc
save MtoPercentage1000%运行一次不容易，把变量全部存储下来
%% 绘图
S=['-ks';'-ko';'-kd';'-kv';'-k*'];
figure;
forkk=1:length(K_set)
    K=K_set(kk);
    M_set=K:5:N;
    L_Mset=length(M_set);
    plot(M_set,Percentage(kk,1:L_Mset),S(kk,:));%绘出x的恢复信号
    hold on;
end
hold off;
xlim([0256]);
legend('K=4','K=12','K=20','K=28','K=36');
xlabel('Number of measurements(M)');
ylabel('Percentage recovered');
title('Percentage of input signals recovered correctly(N=256)(Gaussian)');

　　这段代码指的是固定稀疏度的情况下，研究测量次数与重构概率的关系，突然间不知道测量次数指什么。观测矩阵大小为M*N，测量次数也就是指的这个M的大小，也就是我们压缩采样的采样点数。

　　8-14行代码都是初始化，但是第14行代码，Percentage = zeros(length(K_set),N);为什么维度要这样设置呢？我们要得出的图形是以测量次数M为横坐标，重构概率为纵坐标的，测量次数最大为数据的长度，也就是N，因为我们在仿真中对不同稀疏度的情况进行了仿真，共仿真5种不同稀疏度的情况，所以行数为5，即length（K_set）

　　接着在第17行进入了主循环，第19行M_set = K:5:N；没必要全部遍历，所以每隔5个对该点的值进行测试，但为什么要从K开始呢？K指的是信号的稀疏度，就是信号x最多的非零元素，所以我们进行观测的时候最少要观测到所有非零元素，所以从K开始。执行完这行代码之后生成一个测量次数的行向量，注意不同稀疏度下的测量次数集合是不同的。

　　选择了此次测试的稀疏度后，第21行代码开始对该稀疏度下的测量次数与重构精度的关系进行了测试。依次 选择测量次数集合M_set中的测量次数，第23行初始化P=0，后面如果残差小于某一个值时，即重构成功时，P+1。每个观测值重复1000次操作。

　　第25到32行是生成稀疏信号并进行OMP重构，得到重构后的信号。

　　第37行代码，重复试验1000次后，记录下当前测量次数下的恢复概率，P指的是重构成功的个数，除以1000次试验次数再乘上100即得到重构的概率。

　　接着进行下一个观测次数的循环。

　　M_set集合中的测量次数全部执行完毕后，执行第39行代码：Percentage(kk,1:length(M_set)) = PercentageK，将此次稀疏度下测得的重构概率保存到Percentage中，Percentage的行数是稀疏度的个数，列数是测量次数的个数。

　　第44行代码开始是绘图，根据稀疏度先得到测量次数的集合，然后以测量次数M为横轴，重构概率为纵轴绘制图形。

　　本程序运行结果：

　　文献中的Fig.1：

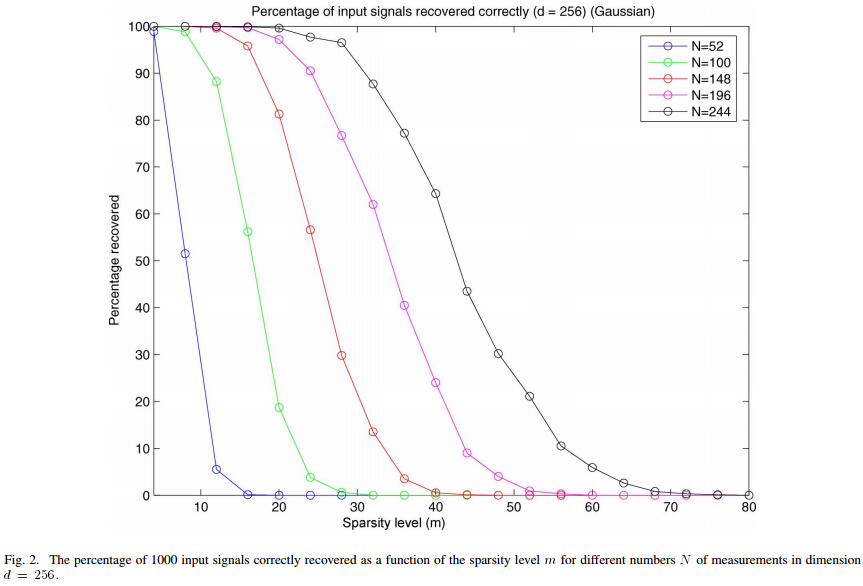
5、信号稀疏度K与重构成功概率关系曲线绘制例程代码

代码与4中的类似

 %压缩感知重构算法测试CS_Reconstuction_KtoPercentage.m
 %   绘制参考文献中的Fig.2
 %   参考文献：Joel A. Tropp and Anna C. Gilbert
 %   Signal Recovery From Random Measurements Via Orthogonal Matching
 %   Pursuit，IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 53, NO. 12,
 %   DECEMBER 2007.
 %   Elapsed time is 1448.966882 seconds.(@20150418night)
 clear all;close all;clc;
 %% 参数配置初始化
 CNT=1000;%对于每组(K,M,N)，重复迭代次数
 N=256;%信号x的长度
 Psi=eye(N);%x本身是稀疏的，定义稀疏矩阵为单位阵x=Psi*theta
 M_set=[52,100,148,196,244];%测量值集合
 Percentage=zeros(length(M_set),N);%存储恢复成功概率
 %% 主循环，遍历每组(K,M,N)
 tic
 formm=1:length(M_set)
     M=M_set(mm);%本次测量值个数
     K_set=1:5:ceil(M/2);%信号x的稀疏度K没必要全部遍历，每隔5测试一个就可以了
     PercentageM=zeros(1,length(K_set));%存储此测量值M下不同K的恢复成功概率
    forkk=1:length(K_set)
        K=K_set(kk);%本次信号x的稀疏度K
        P=0;
       forcnt=1:CNT%每个观测值个数均运行CNT次
             Index_K=randperm(N);
             x=zeros(N,1);
             x(Index_K(1:K))=5*randn(K,1);%x为K稀疏的，且位置是随机的
             Phi=randn(M,N);%测量矩阵为高斯矩阵
             A=Phi*Psi;%传感矩阵
             y=Phi*x;%得到观测向量y
             theta=CS_OMP(y,A,K);%恢复重构信号theta
             x_r=Psi*theta;% x=Psi * theta
            ifnorm(x_r-x)<1e-6%如果残差小于1e-6则认为恢复成功
                 P=P+1;
            end
       end
        PercentageM(kk)=P/CNT*100;%计算恢复概率
    end
     Percentage(mm,1:length(K_set))=PercentageM;
 end
 toc
 save KtoPercentage1000test%运行一次不容易，把变量全部存储下来
 %% 绘图
 S=['-ks';'-ko';'-kd';'-kv';'-k*'];
 figure;
 formm=1:length(M_set)
     M=M_set(mm);
     K_set=1:5:ceil(M/2);
     L_Kset=length(K_set);
     plot(K_set,Percentage(mm,1:L_Kset),S(mm,:));%绘出x的恢复信号
     hold on;
 end
 hold off;
 xlim([0125]);
 legend('M=52','M=100','M=148','M=196','M=244');
 xlabel('Sparsity level(K)');
 ylabel('Percentage recovered');
 title('Percentage of input signals recovered correctly(N=256)(Gaussian)');　

 

　　本程序运行结果：

　　文献中的Fig.2：