外部排序&多路归并排序

外部排序：

一、定义问题

外部排序指的是大文件的排序，即待排序的记录存储在外存储器上，待排序的文件无法一次装入内存，需要在内存和外部存储器之间进行多次数据交换，以达到排序 整个文件的目的。外部排序最常用的算法是多路归并排序，即将原文件分解成多个能够一次性装入内存的部分，分别把每一部分调入内存完成排序。然后，对已经排 序的子文件进行多路归并排序。

二、处理过程

（1）按可用内存的大小，把外存上含有n个记录的文件分成若干个长度为L的子文件，把这些子文件依次读入内存，并利用有效的内部排序方法对它们进行排序，再将排序后得到的有序子文件重新写入外存；

（2）对这些有序子文件逐趟归并，使其逐渐由小到大，直至得到整个有序文件为止。

先从一个例子来看外排序中的归并是如何进行的？
  假设有一个含10000 个记录的文件，首先通过10 次内部排序得到10 个初始归并段R1～R10 ，其中每一段都含1000 个记录。然后对它们作如图10.11 所示的两两归并，直至得到一个有序文件为止 如下图

三 、多路归并排序算法以及败者树

多路归并排序算法在常见数据结构书中都有涉及。从2路到多路（k路），增大k可以减少外存信息读写时间，但k个归并段中选取最小的记录需要比较k-1次， 为得到u个记录的一个有序段共需要(u-1)(k-1)次，若归并趟数为s次，那么对n个记录的文件进行外排时，内部归并过程中进行的总的比较次数为 s(n-1)(k-1)，也即(向上取整)(logkm)(k-1)(n-1)=(向上取整)(log2m/log2k)(k-1)(n-1)，而(k- 1)/log2k随k增而增因此内部归并时间随k增长而增长了，抵消了外存读写减少的时间，这样做不行，由此引出了“败者树”tree of loser的使用。在内部归并过程中利用败者树将k个归并段中选取最小记录比较的次数降为(向上取整)(log2k)次使总比较次数为(向上取整) (log2m)(n-1)，与k无关。

败者树是完全二叉树， 因此数据结构可以采用一维数组。其元素个数为k个叶子结点、k-1个比较结点、1个冠军结点共2k个。ls[0]为冠军结点，ls[1]--ls[k- 1]为比较结点，ls[k]--ls[2k-1]为叶子结点（同时用另外一个指针索引b[0]--b[k-1]指向）。另外bk为一个附加的辅助空间，不 属于败者树，初始化时存着MINKEY的值。

多路归并排序算法的过程大致为：

1）：首先将k个归并段中的首元素关键字依次存入b[0]--b[k-1]的叶子结点空间里，然后调用CreateLoserTree创建败者树，创建完毕之后最小的关键字下标（即所在归并段的序号）便被存入ls[0]中。然后不断循环：

2）把ls[0]所存最小关键字来自于哪个归并段的序号得到为q，将该归并段的首元素输出到有序归并段里，然后把下一个元素关键字放入上一个元素本来所 在的叶子结点b[q]中，调用Adjust顺着b[q]这个叶子结点往上调整败者树直到新的最小的关键字被选出来，其下标同样存在ls[0]中。循环这个 操作过程直至所有元素被写到有序归并段里。

---

外部排序之多路归并

该外部排序上场了.
外部排序干嘛的？

1. 内存极少的情况下，利用分治策略，利用外存保存中间结果，再用多路归并来排序;

1. map-reduce的嫡系.

1.分

内存中维护一个极小的核心缓冲区bigdata按行读入，搜集到memBuffer中的数据调用内排进行排序，排序后将有序结果写入磁盘文件
循环利用

2.合

现在有了n个有序的小文件，怎么合并成1个有序的大文件？
把所有小文件读入内存，然后内排？
(⊙o⊙)…
no!

利用如下原理进行归并排序：

我们举个简单的例子：

文件1：3,6,9
文件2：2,4,8
文件3：1,5,7

第一回合：
文件1的最小值：3 , 排在文件1的第1行
文件2的最小值：2，排在文件2的第1行
文件3的最小值：1，排在文件3的第1行
那么，这3个文件中的最小值是：min(1,2,3) = 1
也就是说，最终大文件的当前最小值，是文件1、2、3的当前最小值的最小值，绕么？
上面拿出了最小值1，写入大文件.

第二回合：
文件1的最小值：3 , 排在文件1的第1行
文件2的最小值：2，排在文件2的第1行
文件3的最小值：5，排在文件3的第2行
那么，这3个文件中的最小值是：min(5,2,3) = 2
将2写入大文件.

也就是说，最小值属于哪个文件，那么就从哪个文件当中取下一行数据.（因为小文件内部有序，下一行数据代表了它当前的最小值）

---

败者树可以改善时间复杂度：

胜者树与败者树  

胜者树和败者树都是完全二叉树，是树形选择排序的一种变型。每个叶子结点相当于一个选手，每个中间结点相当于一场比赛，每一层相当于一轮比赛。

不同的是，胜者树的中间结点记录的是胜者的标号；而败者树的中间结点记录的败者的标号。

胜者树与败者树可以在log(n)的时间内找到最值。任何一个叶子结点的值改变后，利用中间结点的信息，还是能够快速地找到最值。在k路归并排序中经常用到。

一、胜者树

胜者树的一个优点是，如果一个选手的值改变了，可以很容易地修改这棵胜者树。只需要沿着从该结点到根结点的路径修改这棵二叉树，而不必改变其他比赛的结果。

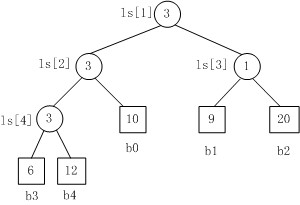
Fig. 1

Fig.1是一个胜者树的示例。规定数值小者胜。

1.         b3 PK b4，b3胜b4负，内部结点ls[4]的值为3；

2.         b3 PK b0，b3胜b0负，内部结点ls[2]的值为3；

3.         b1 PK b2，b1胜b2负，内部结点ls[3]的值为1；

4.         b3 PK b1，b3胜b1负，内部结点ls[1]的值为3。.

当Fig. 1中叶子结点b3的值变为11时，重构的胜者树如Fig. 2所示。

1.         b3 PK b4，b3胜b4负，内部结点ls[4]的值为3；

2.         b3 PK b0，b0胜b3负，内部结点ls[2]的值为0；

3.         b1 PK b2，b1胜b2负，内部结点ls[3]的值为1；

4.         b0 PK b1，b1胜b0负，内部结点ls[1]的值为1。.

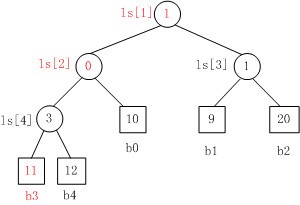
Fig. 2

二、败者树

败者树是胜者树的一种变体。在败者树中，用父结点记录其左右子结点进行比赛的败者，而让胜者参加下一轮的比赛。败者树的根结点记录的是败者，需要加一个结点来记录整个比赛的胜利者。采用败者树可以简化重构的过程。

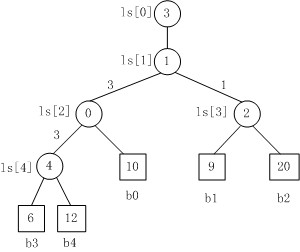
Fig. 3

Fig. 3是一棵败者树。规定数大者败。

1.         b3 PK b4，b3胜b4负，内部结点ls[4]的值为4；

2.         b3 PK b0，b3胜b0负，内部结点ls[2]的值为0；

3.         b1 PK b2，b1胜b2负，内部结点ls[3]的值为2；

4.         b3 PK b1，b3胜b1负，内部结点ls[1]的值为1；

5.         在根结点ls[1]上又加了一个结点ls[0]=3，记录的最后的胜者。

败者树重构过程如下：

·            将新进入选择树的结点与其父结点进行比赛：将败者存放在父结点中；而胜者再与上一级的父结点比较。

·            比赛沿着到根结点的路径不断进行，直到ls[1]处。把败者存放在结点ls[1]中，胜者存放在ls[0]中。

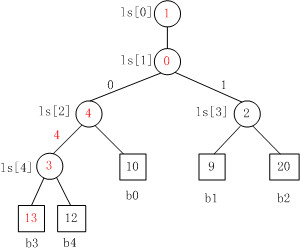
Fig. 4

Fig. 4是当b3变为13时，败者树的重构图。

注意，败者树的重构跟胜者树是不一样的，败者树的重构只需要与其父结点比较。对照Fig.
3来看，b3与结点ls[4]的原值比较，ls[4]中存放的原值是结点4，即b3与b4比较，b3负b4胜，则修改ls[4]的值为结点3。同理，以此
类推，沿着根结点不断比赛，直至结束。

由上可知，败者树简化了重构。败者树的重构只是与该结点的父结点的记录有关，而胜者树的重构还与该结点的兄弟结点有关。

二 使用败者树加快合并排序

外部排序最耗时间的操作时磁盘读写，对于有m个初始归并段，k路平衡的归并排序，磁盘读写次数为

|logkm|，可见增大k的值可以减少磁盘读写的次数，但增大k的值也会带来负面效应，即进行k路合并

的时候会增加算法复杂度，来看一个例子。

把n个整数分成k组，每组整数都已排序好，现在要把k组数据合并成1组排好序的整数，求算法复杂度

u1: xxxxxxxx

u2: xxxxxxxx

u3: xxxxxxxx

.......

uk: xxxxxxxx

算法的步骤是：每次从k个组中的首元素中选一个最小的数，加入到新组，这样每次都要比较k-1次，故

算法复杂度为O((n-1)*(k-1))，而如果使用败者树，可以在O(logk)的复杂度下得到最小的数，算法复杂

度将为O((n-1)*logk)， 对于外部排序这种数据量超大的排序来说，这是一个不小的提高。