数据结构（三十四）最短路径（Dijkstra、Floyd）

　　一、最短路径的定义

　　在网图和非网图中，最短路径的含义是不同的。由于非网图没有边上的权值，所谓的最短路径，其实就是指两顶点之间经过的边数最少的路径；而对于网图来说，最短路径是指两顶点之间经过的边上权值之和最少的路径，并且称路径上的第一个顶点是源点，第二个顶点是终点。显然，非网图可以理解为所有的边的权值都为1的网图。

　　二、Dijkstra算法

　　1.Dijkstra算法描述

　　有向网中从源点V0到其他终点的最短路径的过程是：初始情况下，若从源点到该顶点有弧，则存在一条路径，路径长度即为该弧上的权值。每求得一条到达某个终点w的最短路径，就需要检查是否存在经过这个顶点w的其他路径（即是否存在从顶点w出发到尚未求得最短路径顶点的弧），若存在，判断其长度是否比当前求得的路径长度短，若是，则修改当前路径。同时，保存当前已得到的从源点到各个终点的最短路径。

　　2.Dijkstra算法的C语言代码实现

/*  Dijkstra算法，求有向网G的v0顶点到其余顶点v的最短路径P[v]及带权长度D[v] */
/*  P[v]的值为前驱顶点下标,D[v]表示v0到v的最短路径长度和 */
void ShortestPath_Dijkstra(MGraph G, int v0, Patharc *P, ShortPathTable *D)
{
    int v,w,k,min;
    int final[MAXVEX];/* final[w]=1表示求得顶点v0至vw的最短路径 */
    for(v=; v<G.numVertexes; v++)    /* 初始化数据 */
    {
        final[v] = ;            /* 全部顶点初始化为未知最短路径状态 */
        (*D)[v] = G.arc[v0][v];/* 将与v0点有连线的顶点加上权值 */
        (*P)[v] = -;                /* 初始化路径数组P为-1  */
    }
 
    (*D)[v0] = ;  /* v0至v0路径为0 */
    final[v0] = ;    /* v0至v0不需要求路径 */
    /* 开始主循环，每次求得v0到某个v顶点的最短路径 */
    for(v=; v<G.numVertexes; v++)
    {
        min=INFINITY;    /* 当前所知离v0顶点的最近距离 */
        for(w=; w<G.numVertexes; w++) /* 寻找离v0最近的顶点 */
        {
            if(!final[w] && (*D)[w]<min)
            {
                k=w;
                min = (*D)[w];    /* w顶点离v0顶点更近 */
            }
        }
        final[k] = ;    /* 将目前找到的最近的顶点置为1 */
        for(w=; w<G.numVertexes; w++) /* 修正当前最短路径及距离 */
        {
            /* 如果经过v顶点的路径比现在这条路径的长度短的话 */
            if(!final[w] && (min+G.arc[k][w]<(*D)[w]))
            { /*  说明找到了更短的路径，修改D[w]和P[w] */
                (*D)[w] = min + G.arc[k][w];  /* 修改当前路径长度 */
                (*P)[w]=k;
            }
        }
    }
}

Dijkstra算法

　　3.Dijkstra算法算法的Java语言代码实现

package bigjun.iplab.adjacencyMatrix;
 
public class TheShortestPath_Dijkstra {
 
    private static int[] P;            // 若P[v]=w，则表示V0到Vv的最短路径上，顶点Vv的前驱是Vw
    private static int[] D;            // V0到其他各个顶点的最小权值
    public final static int INFINITY = Integer.MAX_VALUE;
 
    public static void Dijkstra(AdjacencyMatrixGraphINF G, Object V0) throws Exception {
 
        int v;
        int v0 = G.locateVex(V0);
        int vexNum = G.getVexNum();                  // 顶点数
        P = new int[vexNum];
        D = new int[vexNum];
        boolean[] finish = new boolean[vexNum];        // finish[v]=true时，说明已经求得了从v0到v的最短路径
        for (v = 0; v < vexNum; v++) {
            finish[v] = false;
            D[v] = G.getArcs()[v0][v];
            P[v] = -1;
        }
        D[v0] = 0;
        finish[v0] = true;                    // 已求得v0到v0的最短路径
        v = -1;
        for (int i = 1; i < vexNum; i++) {    // 求得V0到顶点Vi的最短路径
            int min = INFINITY;
            for (int w = 0; w < vexNum; w++) {    // 求得当前到v0顶点的最近距离
                if (!finish[w]) {
                    if (D[w] < min) {
                        v = w;
                        min = D[w];
                    }
                }
            }
            finish[v] = true;
            // 在已知V0与V[v]的最短路径的基础上，对V
            for (int w = 0; w < vexNum; w++) {    // 更新当前最短路径及距离
                if (!finish[w] && G.getArcs()[v][w] < INFINITY && (min + G.getArcs()[v][w] < D[w])) {
                    D[w] = min + G.getArcs()[v][w];
                    P[w] = v;
                }
            }
        }
        System.out.println("V0到其他各个顶点的最短路径的权值之和为: ");
        for (int i = 1; i < D.length; i++) {
            System.out.println("V0-" + G.getVex(i).toString() + ": " + D[i]);
        }
        System.out.println();
        System.out.println("V0到其他各个顶点的最短路径的倒序为: ");
        for (int i = 1; i < vexNum; i++) {
            System.out.print("从" + G.getVex(i) + "到V0的最短路径为: ");
            int j = i;
            while (P[j] != -1) {
                System.out.print(G.getVex(P[j]) + " ");
                j=P[j];
            }
            System.out.println();
        }
    }
 
}

　　4.Dijkstra算法执行过程的举例说明

　　以下面的图为例：

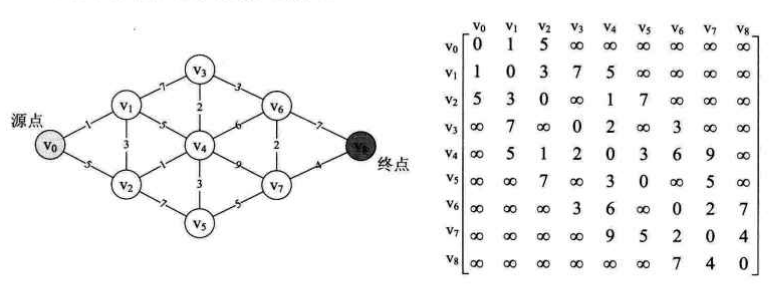
　　测试类：

    // 手动创建一个用于测试最短路径算法的无向网
    public static AdjacencyMatrixGraphINF createUDNByYourHand_ForTheShortestPath() {
        Object vexs_UDN[] = {"V0", "V1", "V2", "V3", "V4", "V5", "V6", "V7", "V8"};
        int arcsNum_UDN = 16;
        int[][] arcs_UDN = new int[vexs_UDN.length][vexs_UDN.length];
        for (int i = 0; i < vexs_UDN.length; i++)         // 构造无向图邻接矩阵
            for (int j = 0; j < vexs_UDN.length; j++)
                if (i==j) {
                    arcs_UDN[i][j]=0;
                } else {
                    arcs_UDN[i][j] = arcs_UDN[i][j] = INFINITY;
                }
 
        arcs_UDN[0][1] = 1;
        arcs_UDN[0][2] = 5;
        arcs_UDN[1][2] = 3;
        arcs_UDN[1][3] = 7;
        arcs_UDN[1][4] = 5;
        arcs_UDN[2][4] = 1;
        arcs_UDN[2][5] = 7;
        arcs_UDN[3][4] = 2;
        arcs_UDN[3][6] = 3;
        arcs_UDN[4][5] = 3;
        arcs_UDN[4][6] = 6;
        arcs_UDN[4][7] = 9;
        arcs_UDN[5][7] = 5;
        arcs_UDN[6][7] = 2;
        arcs_UDN[6][8] = 7;
        arcs_UDN[7][8] = 4;
 
        for (int i = 0; i < vexs_UDN.length; i++)         // 构造无向图邻接矩阵
            for (int j = i; j < vexs_UDN.length; j++)
                arcs_UDN[j][i] = arcs_UDN[i][j];
        return new AdjMatGraph(GraphKind.UDN, vexs_UDN.length, arcsNum_UDN, vexs_UDN, arcs_UDN);
    }
 
    public static void main(String[] args) throws Exception {
 
        AdjMatGraph UDN_Graph_TSP = (AdjMatGraph) createUDNByYourHand_ForTheShortestPath();
        TheShortestPath_Dijkstra.Dijkstra(UDN_Graph_TSP, "V0");
    }

　　输出：

V0到其他各个顶点的最短路径的权值之和为:
V0-V1: 1
V0-V2: 4
V0-V3: 7
V0-V4: 5
V0-V5: 8
V0-V6: 10
V0-V7: 12
V0-V8: 16
 
V0到其他各个顶点的最短路径的倒序为:
从V1到V0的最短路径为:
从V2到V0的最短路径为: V1
从V3到V0的最短路径为: V4 V2 V1
从V4到V0的最短路径为: V2 V1
从V5到V0的最短路径为: V4 V2 V1
从V6到V0的最短路径为: V3 V4 V2 V1
从V7到V0的最短路径为: V6 V3 V4 V2 V1
从V8到V0的最短路径为: V7 V6 V3 V4 V2 V1

　　结合例子分析代码执行过程：

初始化：
v0=0，finish数组都为false，说明所有的点都未求得最短路径，D数组是第一行的权值，P00,10,20,11,22,33为true，D[0]=0,finish[0]= true,v=-1
i=1时，此时D={0,1,5,INF,INF,INF,INF,INF,INF},finish={TFFFFFFFF},v=1,min=D[1]=1,finish[1]=true,
　　　　现在V0-V1-V2=D[2]=min+3=4,V0-V1-V3=D[3]=min+7=8,V0-V1-V4=D[4]=min+5=6,
　　　　p2=1,p3=1,p4=1
i=2时，此时D={0,1,4,8,6,INF,INF,INF,INF},finish={TTFFFFFFF},v=2,min=D[2]=4,finish[2]=true,
　　　　现在V0-V2-V4=D[4]=4+1=5,V0-V2-V5=D[5]=4+7=11,
　　　　p4=2,p5=2
i=3时，此时D={0,1,4,8,5,11,INF,INF,INF},finish={TTTFFFFFF},v=4,min=D[4]=5,finish[4]=true,
　　　　V0-V4-V3=D[3]=5+2=7,V0-V4-V5=D[5]=5+3=8,V0-V4-V6=D[6]=5+6=11，V0-V4-V7=D[7]=5+9=14，
　　　　p3=4,p5=4,p6=4,p7=4
...
i=8时，此时D={0,1,4,7,5,8,10,12,16},finish={TTTTTTTTF},v=8,min=D[8]=16,finish[8]=true,
此时，数组p为：[0,0,1,4,2,4,3,6,7]即由于p8=7,p7=6,p6=3,p3=4,p4=2,p2=1,p1=0得到从V8到V0的倒序为：V8-V7-V6-V3-V4-V2-V1-V0

　　三、Floyd算法

　　1.Floyd算法描述

　　Floyd算法适用于要求所有顶点至所有顶点的最短路径的。其算法思路是：

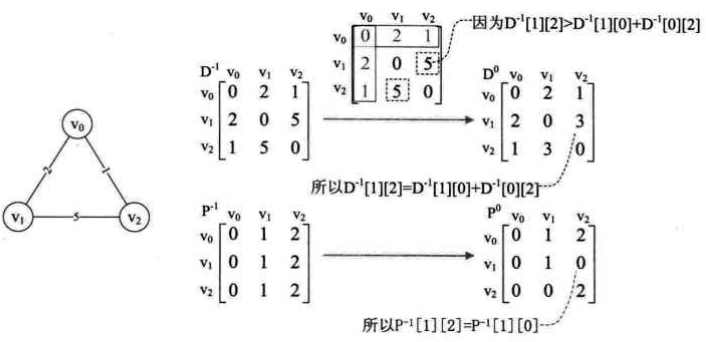
　　首先定义左边两个矩阵D和P，D矩阵表示顶点到顶点的最短路径权值之和，P矩阵表示顶点的最小路径的前驱矩阵。

　　例如，从v1-v0-v2时，从D矩阵可以看出，D[1][0]+D[0][2]=2+1=3，而D[1][2]=5，也就说明v1先到v0再到v2的路径比v1直接到v2的路径权值和要小，所以就要更新D矩阵的[1][2]和[2][1]的值为更小的权值和3，同时由于v1到v2需要经过v0，所以P[1][2]=P[2][1]=0　　

　　2.Floyd算法的C语言代码实现

#include "stdio.h"
#include "stdlib.h"
#include "io.h"
#include "math.h"
#include "time.h"
 
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXEDGE 20
#define MAXVEX 20
#define INFINITY 65535
 
typedef int Status;    /* Status是函数的类型,其值是函数结果状态代码，如OK等 */
 
typedef struct
{
    int vexs[MAXVEX];
    int arc[MAXVEX][MAXVEX];
    int numVertexes, numEdges;
}MGraph;
 
typedef int Patharc[MAXVEX][MAXVEX];
typedef int ShortPathTable[MAXVEX][MAXVEX];
 
/* 构件图 */
void CreateMGraph(MGraph *G)
{
    int i, j;
 
    /* printf("请输入边数和顶点数:"); */
    G->numEdges=;
    G->numVertexes=;
 
    for (i = ; i < G->numVertexes; i++)/* 初始化图 */
    {
        G->vexs[i]=i;
    }
 
    for (i = ; i < G->numVertexes; i++)/* 初始化图 */
    {
        for ( j = ; j < G->numVertexes; j++)
        {
            if (i==j)
                G->arc[i][j]=;
            else
                G->arc[i][j] = G->arc[j][i] = INFINITY;
        }
    }
 
    G->arc[][]=;
    G->arc[][]=;
    G->arc[][]=;
    G->arc[][]=;
    G->arc[][]=; 
 
    G->arc[][]=;
    G->arc[][]=;
    G->arc[][]=;
    G->arc[][]=;
    G->arc[][]=;
 
    G->arc[][]=;
    G->arc[][]=;
    G->arc[][]=;
    G->arc[][]=;
    G->arc[][]=;
 
    G->arc[][]=;
 
    for(i = ; i < G->numVertexes; i++)
    {
        for(j = i; j < G->numVertexes; j++)
        {
            G->arc[j][i] =G->arc[i][j];
        }
    }
 
}
 
/* Floyd算法，求网图G中各顶点v到其余顶点w的最短路径P[v][w]及带权长度D[v][w]。 */
void ShortestPath_Floyd(MGraph G, Patharc *P, ShortPathTable *D)
{
    int v,w,k;
    for(v=; v<G.numVertexes; ++v) /* 初始化D与P */
    {
        for(w=; w<G.numVertexes; ++w)
        {
            (*D)[v][w]=G.arc[v][w];    /* D[v][w]值即为对应点间的权值 */
            (*P)[v][w]=w;                /* 初始化P */
        }
    }
    for(k=; k<G.numVertexes; ++k)
    {
        for(v=; v<G.numVertexes; ++v)
        {
            for(w=; w<G.numVertexes; ++w)
            {
                if ((*D)[v][w]>(*D)[v][k]+(*D)[k][w])
                {/* 如果经过下标为k顶点路径比原两点间路径更短 */
                    (*D)[v][w]=(*D)[v][k]+(*D)[k][w];/* 将当前两点间权值设为更小的一个 */
                    (*P)[v][w]=(*P)[v][k];/* 路径设置为经过下标为k的顶点 */
                }
            }
        }
    }
}
 
int main(void)
{
    int v,w,k;
    MGraph G;    
 
    Patharc P;
    ShortPathTable D; /* 求某点到其余各点的最短路径 */   
 
    CreateMGraph(&G);
 
    ShortestPath_Floyd(G,&P,&D);  
 
    printf("各顶点间最短路径如下:\n");
    for(v=; v<G.numVertexes; ++v)
    {
        for(w=v+; w<G.numVertexes; w++)
        {
            printf("v%d-v%d weight: %d ",v,w,D[v][w]);
            k=P[v][w];                /* 获得第一个路径顶点下标 */
            printf(" path: %d",v);    /* 打印源点 */
            while(k!=w)                /* 如果路径顶点下标不是终点 */
            {
                printf(" -> %d",k);    /* 打印路径顶点 */
                k=P[k][w];            /* 获得下一个路径顶点下标 */
            }
            printf(" -> %d\n",w);    /* 打印终点 */
        }
        printf("\n");
    }
 
    printf("最短路径D\n");
    for(v=; v<G.numVertexes; ++v)
    {
        for(w=; w<G.numVertexes; ++w)
        {
            printf("%d\t",D[v][w]);
        }
        printf("\n");
    }
    printf("最短路径P\n");
    for(v=; v<G.numVertexes; ++v)
    {
        for(w=; w<G.numVertexes; ++w)
        {
            printf("%d ",P[v][w]);
        }
        printf("\n");
    }
 
    return ;
}

最短路径算法之Floyd算法

　　3.Floyd算法算法的Java语言代码实现

package bigjun.iplab.adjacencyMatrix;
 
public class TheShortestPath_Floyd {
 
    private static int[][] D;            // 顶点到顶点的最短路径权值和矩阵
    private static int[][] P;            // 顶点的到顶点的最短路径的前驱矩阵
    public final static int INFINITY = Integer.MAX_VALUE;
 
    public static void Floyd(AdjacencyMatrixGraphINF G) throws Exception {
 
        int v, w ,k;
        int vexNum = G.getVexNum();
        P = new int[vexNum][vexNum];
        D = new int[vexNum][vexNum];
        for (v = 0; v < vexNum; v++) {
            for (w = 0; w < vexNum; w++) {
                D[v][w] = G.getArcs()[v][w];    // 初始化D矩阵为邻接矩阵
                P[v][w] = w;                    // 初始化P矩阵，表示从v到w的最短路径的前驱是w，即直接到达的意思
            }
        }
        for (k = 0; k < vexNum; k++) {            // k值表示中转顶点的下标
            for (v = 0; v < vexNum; v++) {        // v值表示起始顶点的下标
                for (w = 0; w < vexNum; w++) {    // w值表示终止顶点的下标
                    if (D[v][k] < INFINITY && D[k][w] < INFINITY &&    // 注意: 只限定两个不是正无穷就可以，否则会造成越界的情况
                        D[v][w] > D[v][k] + D[k][w]) {    // 从v直接到w的权值和大于从v先到k再到w
                        D[v][w] = D[v][k] + D[k][w];    // 更新从v到w的权值和
                        P[v][w] = P[v][k];                // 路径设置为经过下标为k的顶点
                    }
                }
            }
        }
 
        System.out.println("D矩阵为: ");
        for (v = 0; v < vexNum; v++) {
            for (w = 0; w < vexNum; w++) {
                System.out.print(D[v][w] + " ");
            }
            System.out.println();
        }
        System.out.println();
 
        System.out.println("P矩阵为: ");
        for (v = 0; v < vexNum; v++) {
            for (w = 0; w < vexNum; w++) {
                System.out.print(P[v][w] + " ");
            }
            System.out.println();
        }
        System.out.println();
 
        System.out.println("各个顶点之间的最短路径的权值和为: ");
        for (v = 0; v < vexNum; v++) {
            for (w = v + 1; w < vexNum; w++) {
                System.out.print(G.getVex(v) + "-");
                System.out.print(G.getVex(w) + " weight: ");
                System.out.println(D[v][w]);
            }
        }
        System.out.println();
 
        System.out.println("各个顶点之间的最短路径为: ");
        for (v = 0; v < vexNum; v++) {
            for (w = v + 1; w < vexNum; w++) {
                System.out.print(G.getVex(v) + "->");
                System.out.print(G.getVex(w) + " TheShortestPath: ");
                k = P[v][w];            // 获得第一个路径顶点下标
                System.out.print(G.getVex(v));
                while (k!=w) {
                    System.out.print("->" + G.getVex(k));
                    k = P[k][w];
                }
                System.out.println("->" + G.getVex(w));
            }
        }
        System.out.println();
    }
}

　　4.Floyd算法执行过程的举例说明

　　以下面的图为例：

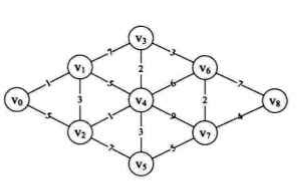
　　测试代码为：

    // 手动创建一个用于测试最短路径算法的无向网
    public static AdjacencyMatrixGraphINF createUDNByYourHand_ForTheShortestPath() {
        Object vexs_UDN[] = {"V0", "V1", "V2", "V3", "V4", "V5", "V6", "V7", "V8"};
        int arcsNum_UDN = 16;
        int[][] arcs_UDN = new int[vexs_UDN.length][vexs_UDN.length];
        for (int i = 0; i < vexs_UDN.length; i++)         // 构造无向图邻接矩阵
            for (int j = 0; j < vexs_UDN.length; j++)
                if (i==j) {
                    arcs_UDN[i][j]=0;
                } else {
                    arcs_UDN[i][j] = arcs_UDN[i][j] = INFINITY;
                }
 
        arcs_UDN[0][1] = 1;
        arcs_UDN[0][2] = 5;
        arcs_UDN[1][2] = 3;
        arcs_UDN[1][3] = 7;
        arcs_UDN[1][4] = 5;
        arcs_UDN[2][4] = 1;
        arcs_UDN[2][5] = 7;
        arcs_UDN[3][4] = 2;
        arcs_UDN[3][6] = 3;
        arcs_UDN[4][5] = 3;
        arcs_UDN[4][6] = 6;
        arcs_UDN[4][7] = 9;
        arcs_UDN[5][7] = 5;
        arcs_UDN[6][7] = 2;
        arcs_UDN[6][8] = 7;
        arcs_UDN[7][8] = 4;
 
        for (int i = 0; i < vexs_UDN.length; i++)         // 构造无向图邻接矩阵
            for (int j = i; j < vexs_UDN.length; j++)
                arcs_UDN[j][i] = arcs_UDN[i][j];
        return new AdjMatGraph(GraphKind.UDN, vexs_UDN.length, arcsNum_UDN, vexs_UDN, arcs_UDN);
    }
 
    public static void main(String[] args) throws Exception {
 
        AdjMatGraph UDN_Graph_TSP = (AdjMatGraph) createUDNByYourHand_ForTheShortestPath();
        TheShortestPath_Floyd.Floyd(UDN_Graph_TSP);
　　}

　　输出为：

D矩阵为:
0 1 4 7 5 8 10 12 16
1 0 3 6 4 7 9 11 15
4 3 0 3 1 4 6 8 12
7 6 3 0 2 5 3 5 9
5 4 1 2 0 3 5 7 11
8 7 4 5 3 0 7 5 9
10 9 6 3 5 7 0 2 6
12 11 8 5 7 5 2 0 4
16 15 12 9 11 9 6 4 0 
 
P矩阵为:
0 1 1 1 1 1 1 1 1
0 1 2 2 2 2 2 2 2
1 1 2 4 4 4 4 4 4
4 4 4 3 4 4 6 6 6
2 2 2 3 4 5 3 3 3
4 4 4 4 4 5 7 7 7
3 3 3 3 3 7 6 7 7
6 6 6 6 6 5 6 7 8
7 7 7 7 7 7 7 7 8 
 
各个顶点之间的最短路径的权值和为:
V0-V1 weight: 1
V0-V2 weight: 4
V0-V3 weight: 7
V0-V4 weight: 5
V0-V5 weight: 8
V0-V6 weight: 10
V0-V7 weight: 12
V0-V8 weight: 16
V1-V2 weight: 3
V1-V3 weight: 6
V1-V4 weight: 4
V1-V5 weight: 7
V1-V6 weight: 9
V1-V7 weight: 11
V1-V8 weight: 15
V2-V3 weight: 3
V2-V4 weight: 1
V2-V5 weight: 4
V2-V6 weight: 6
V2-V7 weight: 8
V2-V8 weight: 12
V3-V4 weight: 2
V3-V5 weight: 5
V3-V6 weight: 3
V3-V7 weight: 5
V3-V8 weight: 9
V4-V5 weight: 3
V4-V6 weight: 5
V4-V7 weight: 7
V4-V8 weight: 11
V5-V6 weight: 7
V5-V7 weight: 5
V5-V8 weight: 9
V6-V7 weight: 2
V6-V8 weight: 6
V7-V8 weight: 4
 
各个顶点之间的最短路径为:
V0->V1 TheShortestPath: V0->V1
V0->V2 TheShortestPath: V0->V1->V2
V0->V3 TheShortestPath: V0->V1->V2->V4->V3
V0->V4 TheShortestPath: V0->V1->V2->V4
V0->V5 TheShortestPath: V0->V1->V2->V4->V5
V0->V6 TheShortestPath: V0->V1->V2->V4->V3->V6
V0->V7 TheShortestPath: V0->V1->V2->V4->V3->V6->V7
V0->V8 TheShortestPath: V0->V1->V2->V4->V3->V6->V7->V8
V1->V2 TheShortestPath: V1->V2
V1->V3 TheShortestPath: V1->V2->V4->V3
V1->V4 TheShortestPath: V1->V2->V4
V1->V5 TheShortestPath: V1->V2->V4->V5
V1->V6 TheShortestPath: V1->V2->V4->V3->V6
V1->V7 TheShortestPath: V1->V2->V4->V3->V6->V7
V1->V8 TheShortestPath: V1->V2->V4->V3->V6->V7->V8
V2->V3 TheShortestPath: V2->V4->V3
V2->V4 TheShortestPath: V2->V4
V2->V5 TheShortestPath: V2->V4->V5
V2->V6 TheShortestPath: V2->V4->V3->V6
V2->V7 TheShortestPath: V2->V4->V3->V6->V7
V2->V8 TheShortestPath: V2->V4->V3->V6->V7->V8
V3->V4 TheShortestPath: V3->V4
V3->V5 TheShortestPath: V3->V4->V5
V3->V6 TheShortestPath: V3->V6
V3->V7 TheShortestPath: V3->V6->V7
V3->V8 TheShortestPath: V3->V6->V7->V8
V4->V5 TheShortestPath: V4->V5
V4->V6 TheShortestPath: V4->V3->V6
V4->V7 TheShortestPath: V4->V3->V6->V7
V4->V8 TheShortestPath: V4->V3->V6->V7->V8
V5->V6 TheShortestPath: V5->V7->V6
V5->V7 TheShortestPath: V5->V7
V5->V8 TheShortestPath: V5->V7->V8
V6->V7 TheShortestPath: V6->V7
V6->V8 TheShortestPath: V6->V7->V8
V7->V8 TheShortestPath: V7->V8

　　结合实例分析代码执行过程：

初始化后的D矩阵和P矩阵如上图所示：当K=0时，所有的顶点都经过v0中转，通过计算可以直到没有最短路径的变化
当K=1时，也就是说所有的顶点都经过v1中转，通过比较
　　　　D02=5，  而D01+D12=4，所以D02=5，P02=1，也就是说v0到v2要进过v1
　　　　D03=INF，而D01+D13=8，所以D03=8，P03=1，
　　　　D04=INF，而D01+D14=6，所以D04=6，P04=1，
...同理
要求得v0到v8的路径，已知最后的P矩阵
由p08=1得知要经过v1，由p18=2得知要经过v2，由p28=4得知要经过v4，由p48=3得知要经过v3，由p38=6得知要经过v6，由p68=7得知要经过v7，由p78=8得知要经过v8
从而，得出从v0到v8要经过的路径为：v0-v1-v2-v4-v3-v6-v7-v8
其他同理。

数据结构（三十四）最短路径（Dijkstra、Floyd）的更多相关文章

COJ966 WZJ的数据结构（负三十四）
WZJ的数据结构(负三十四) 难度级别:C: 运行时间限制:20000ms: 运行空间限制:262144KB: 代码长度限制:2000000B 试题描述给一棵n个节点的树,请对于形如"u ...
NeHe OpenGL教程第三十四课：地形
转自[翻译]NeHe OpenGL 教程前言声明,此 NeHe OpenGL教程系列文章由51博客yarin翻译(2010-08-19),本博客为转载并稍加整理与修改.对NeHe的OpenGL管线 ...
JAVA之旅（三十四）——自定义服务端，URLConnection，正则表达式特点，匹配，切割，替换，获取，网页爬虫
JAVA之旅(三十四)--自定义服务端,URLConnection,正则表达式特点,匹配,切割,替换,获取,网页爬虫我们接着来说网络编程,TCP 一.自定义服务端我们直接写一个服务端,让本机去连接 ...
Java进阶(三十四)Integer与int的种种比较你知道多少？
Java进阶(三十四)Integer与int的种种比较你知道多少? 前言如果面试官问Integer与int的区别:估计大多数人只会说到两点:Ingeter是int的包装类,注意是一个类:int的初值 ...
Gradle 1.12用户指南翻译——第三十四章. JaCoCo 插件
本文由CSDN博客万一博主翻译,其他章节的翻译请参见: http://blog.csdn.net/column/details/gradle-translation.html 翻译项目请关注Githu ...
SQL注入之Sqli-labs系列第三十四关（基于宽字符逃逸POST注入）和三十五关
开始挑战第三十四关和第三十五关(Bypass add addslashes) 0x1查看源码本关是post型的注入漏洞,同样的也是将post过来的内容进行了 ' \ 的处理. if(isset($_ ...
spring boot 常见三十四问
Spring Boot 是微服务中最好的 Java 框架. 我们建议你能够成为一名 Spring Boot 的专家. 问题一 Spring Boot.Spring MVC 和 Spring 有什么区别 ...
“全栈2019”Java多线程第三十四章：超时自动唤醒被等待的线程
难度初级学习时间 10分钟适合人群零基础开发语言 Java 开发环境 JDK v11 IntelliJ IDEA v2018.3 文章原文链接 "全栈2019"Java多 ...
第三百三十四节，web爬虫讲解2—Scrapy框架爬虫—Scrapy爬取百度新闻，爬取Ajax动态生成的信息
第三百三十四节,web爬虫讲解2—Scrapy框架爬虫—Scrapy爬取百度新闻,爬取Ajax动态生成的信息 crapy爬取百度新闻,爬取Ajax动态生成的信息,抓取百度新闻首页的新闻rul地址有多 ...
“全栈2019”Java第三十四章：可变参数列表
难度初级学习时间 10分钟适合人群零基础开发语言 Java 开发环境 JDK v11 IntelliJ IDEA v2018.3 文章原文链接 "全栈2019"Java第 ...

随机推荐

暑期——第五周总结（Web连接hbase数据库）
所花时间:7天代码行:1000(python)+250(java) 博客量:1篇了解到知识点 : 在尝试使用hbase当作数据库时,林子雨老师教程中有完整代码关于使用hbase,我就像当然认为只需 ...
linux初学者小记
a开头的小命令 alias命令 # echo=' - - - ' > /sys/class/scsi_host/host0/scan这条命令是咱们在给虚拟机装了一块新的硬盘后,在不关机的前提下扫 ...
Save&Load--Unity存档读档的学习总结
存档与读档功能举例: 传统RPG游戏(仙剑.空之轨迹): 1.角色信息(生命值,等级) 2.道具信息(装备,药品) 3.场景信息(场景名称.角色坐标) 4.事件信息(任务相关) 关卡类游戏:关卡的通 ...
git clone 解决Permission Denied (publickey)问题
本地git bash 使用git clone git@github.com:***.git方式下载github代码至本地时需要依赖ssh key,遇到权限不足问题时一般都是SSH key失效或者SSH ...
3. Git与TortoiseGit基本操作
1. GitHub操作本节先简单介绍 git 的使用与操作, 然后再介绍 TortoiseGit 的使用与操作. 先看看SVN的操作吧, 最常见的是检出(Check out ...), 更新 (U ...
export import 的用法和注意之处
1.整体引入: 会将若干export导出的内容组合成一个对象返回: import *as api from utils.https; api为自定义名称,可直接指定此文件中的某个方法,uti ...
Spark 学习笔记之 aggregateByKey
aggregateByKey: import org.apache.spark.SparkContext import org.apache.spark.rdd.RDD import org.apac ...
docker服务在Mac上的启动与使用
在mac上打开安装的docker软件就可以启动docker服务了点击顶部状态栏中鲸鱼图标会弹出操作菜单,显示着服务的状态,如下图所示: 只有在docker服务启动了之后,才可以在终端使用docker ...
python-setup模块
本地打包,setup安装一.distutils 使用:distutils 进行打包,步骤如下,以单一文件为例. 1.创建文件在同一目录下.写一个foo.py文件: #-*- coding:utf- ...
云上的芯脏病：奇怪的阿里云 RDS 数据库突发 CPU 近 100% 问题
最近遇到了奇怪的阿里云 RDS 数据库突发 CPU 近 100% 问题,遇到了3次. 第一次是10月12日(周六)凌晨 3:24 负载极低的时候开始出现,早上发现后进行了主备切换,恢复了正常. 第二次 ...

数据结构（三十四）最短路径（Dijkstra、Floyd）

数据结构（三十四）最短路径（Dijkstra、Floyd）的更多相关文章

随机推荐

热门专题